A/Bテストは無理だと言われたあなたへ

はじめに

前回の記事では、A/Bテストってそもそもなんだっけ？について解説を試み、A/Bテストが介入施策の因果効果を推定するための強力なツールである所以を紐解きました。しかし、特に医療における介入効果測定（投薬試験や臨床試験）においてA/Bテストを行えない状況が多数存在し得ます。例えば、喫煙が肺がんに及ぼしうる因果効果を知りたい時に、被験者に「1日に〇〇箱タバコを吸え！」と指示することは倫理的に難しいですし、そうでない場合も生身の人間を対象にする実験は、十分なサンプル数を可能なコストのなかで得られるとは限りません。

また、医療だけではなく、広告やレコメンドの因果効果を推定したい時にA/Bテストをすぐに適切に行うことができない状況も存在すると考えられます。（予算の問題、周囲の協力が得られないなど）そのような時に、介入効果の測定を諦めなければならないかというと、そんなことはありません。確かにA/Bテストに比べて強力ではないですが、すでに何らかの（ランダムではない）割り当て基準に基づいて集められた過去のデータ（観察データ）から平均的因果効果（ATE: Average Treatment Effect）を推定するために必要や追加的な仮定や方法論について今回は解説を試みます。

（余談：医療の文脈だとA/Bテストではなく無作為比較試験(RCT: Randomized Controlled Trial)と呼ばれることが多いです。）

目次

1. はじめに
2. A/Bテストができない時の問題点
3. 観察データからATEに迫るには？
4. 傾向スコアによる交絡補正
5. 実データを用いた簡易実験
6. まとめ
7. 次なる問題意識に向けて
8. 参考

A/Bテストができない時の問題点

前回の記事で整理した通り、A/Bテストが強力なATE推定のための実験方法とされる所以は、介入のランダム割り当てによりMean Exchangeabilityが成り立つことが期待されるためでした。これは日本語に落とし込むと「実際に介入を受けた人たちの介入を受けた時の目的変数の期待値が、実際に介入を受けなかった人たちが仮に介入を受けた時の目的変数の期待値と一致することが期待される。（逆もまた然り）」と言い表す事が出来ました。しかし、A/Bテストを行うことができないすなわち、介入のランダムな割り当てを経ていないデータ（観察データ）においては、このMean Exchangeabilityが一般に成り立つことは期待できません。つまり、

E [Y^{(k)} | W_i = 1] \neq E [Y^{(k)} | W_i = 0]  \quad \forall k \in \{0, 1\}

ということになります。

交絡因子の例

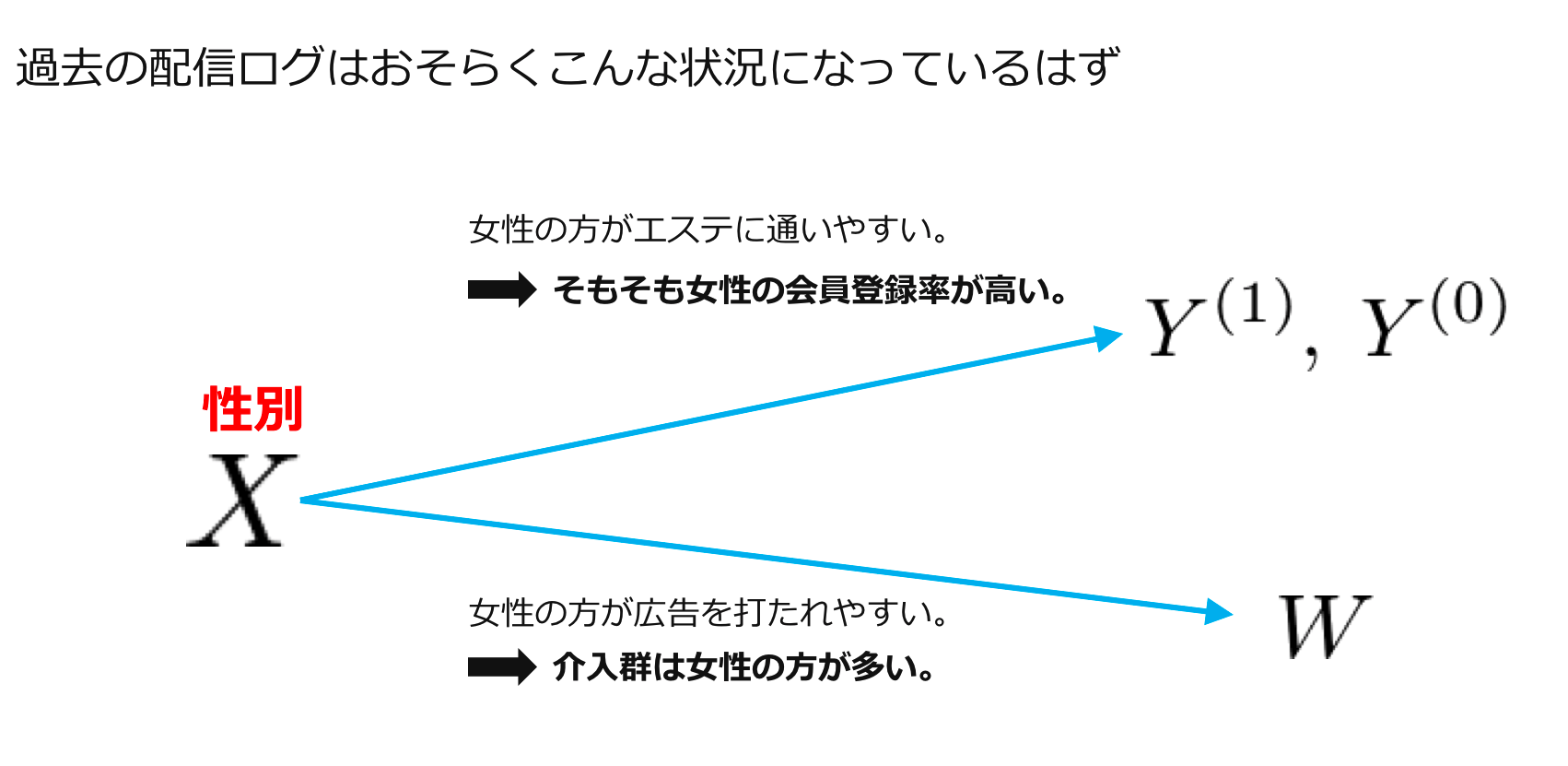
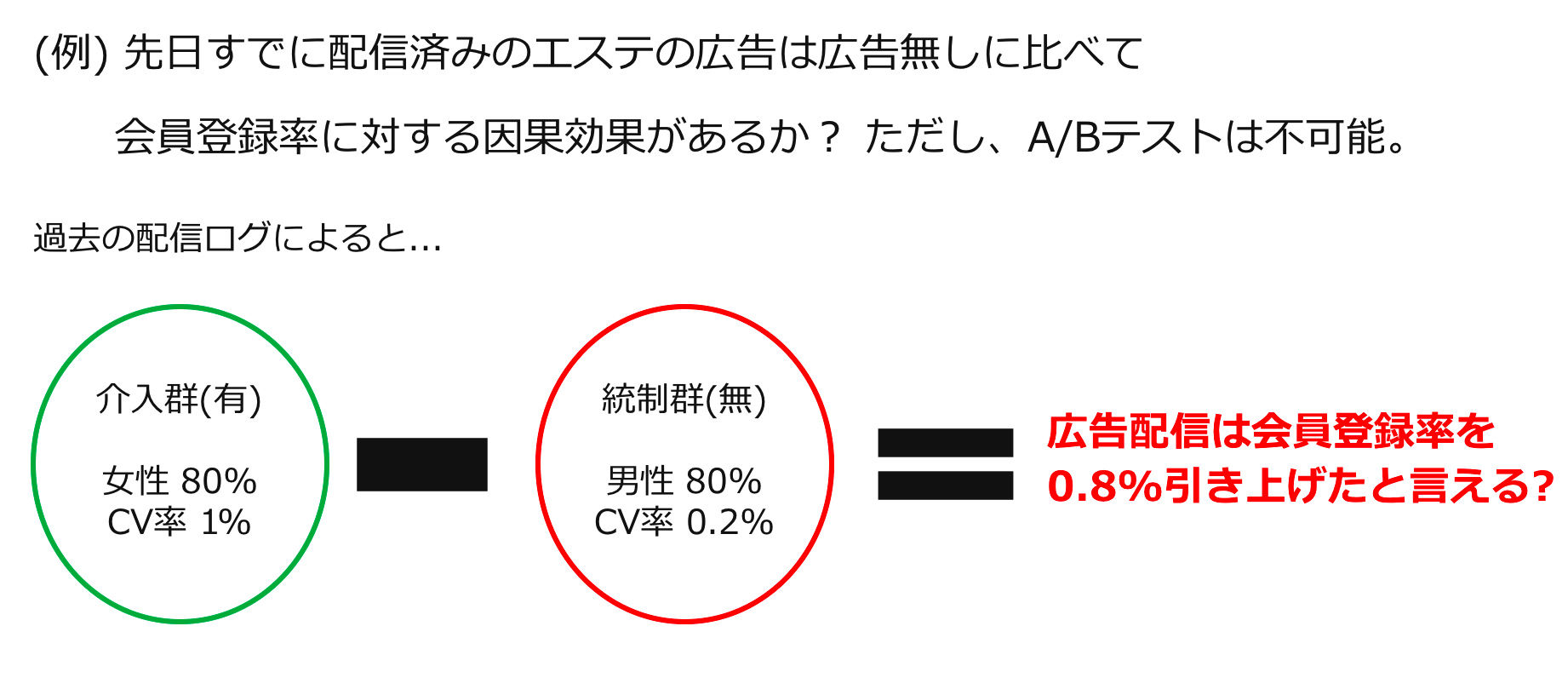
ではこのMean Exchangeabilityが成り立っていないとはどういう状況なのか？どういった不具合をもたらすのか？について具体例と共に見ていきます。ここでは、以下のようなエステの広告配信が広告配信がない場合に比べてどれくらい会員登録率を増加させるか、を知りたいという状況を例として使います。まず設定を以下の図にまとめました。

前回の記事を読んでくださった方はお気づきかもしれませんが、こちらの例でも前回用いた例と同様に、介入群の登録率が1%で統制群の登録率が0.2%だったとしています。前回記事の説明では、このデータがA/Bテストによって集められたことを想定していた上で目的変数の平均の差分が0.8%だったため、介入には正の因果効果が認められるとし、広告を配信するという意思決定に繋がるとしていました。では、今回の例においても同様に群間の会員登録率の差分が0.8%あることから、広告介入には効果があると結論付けて良いのでしょうか？

話の流れからお気づきだと思いますが、答えは「No」です。今回の例ではデータがA/Bテストではなくて、過去の広告配信ログであることを想定しており、その過去の配信ログは以下のような状況にあると思われます。

今、おそらく配信ログに記録が残っているであろうユーザーの性別という特徴量（因果推論の文脈では共変量と呼ばれることが多いので以後はこちらに従います。）に注目します。ここで、過去の配信ログにおける介入割り当てはランダムではなく、会員登録率を最大化しようする施策によって決められているはずです。（このような介入戦略が最適であるかはさておき。）今回の問題設定はエステの会員登録率でしたのでそもそも女性の会員登録率が高いと考えられますが、同時にそんなことは広告の打ち手もわかっているので、女性により多くの広告が打たれていると考えられます。つまり、今注目している性別という共変量は、潜在的目的変数にも介入割り当てにも影響を与える共変量であると言えます。このような共変量のことを交絡因子（confounding factor）と呼んだりしますが、A/Bテストが行えず観察データからATEの推定を行う際に、この交絡因子の存在が非常に厄介になります。さて、一番最初に掲載した図に交絡因子の一つとして考えられる性別の情報を追加してみましょう。

このように、女性の方が介入されやすいという今回の状況設定を加味すると、過去の配信ログにおいて広告を見せられた群のうち8割が女性である一方で、広告を見せられなかった群のうち8割が男性であるといった状況が例えば考えられます。

この辺りまでくると、だんだんMean Exchangeabilityが成り立っていないということがわかってくると思います。Mean Exchangeabilityの前半部分である「実際に介入を受けた人たちの介入を受けた時の目的変数の期待値」は今回のデータにおいても観測されていて、1%ということになります。次に後半部分である「実際に介入を受けなかった人たちが仮に介入を受けた時の目的変数の期待値」について考えます。今回統制群は男性が80%を占めその会員登録率は0.2%でした。しかし、この統制群が仮に介入を受けたとする世界においても、おそらく会員登録率は1%に及ばないでしょう。なぜならば、今回性別は大きく会員登録率に寄与している共変量だと考えられ、男性が多くを占める統制群にもし広告を見せたとして、女性が多くを占める介入群が実際に介入を受けたことにより実現した1%という目的変数には届かないと思われるからです。つまり、観測された目的変数の差分である0.8%が、介入有無の違いによって生まれた差であるのか交絡因子（今回は性別の違い）によって生まれた差であるのか見分けがつかなくなってしまっているのです。

以下の図でまとめるように、A/Bテストが行えず観察データを用いる場合に交絡因子が存在するならば、Mean Exchangeabilityが成り立たないということを具体例とともに見てきました。前回の記事にあるように、データの目的変数の平均の差分からATEを推定することができるためには、Mean Exchangeabilityが成り立っていることが必要でしたので、何らかの工夫により交絡因子をどうにかしないと、観察データからATEを推定することはできなさそうです。

観察データからATEに迫るには？

さて前章で観察データにおいてはMean Exchangeabilityが成り立たないため単純にデータからATEを推定することができないということを具体例とともに見ました。そのような望ましくない状況が起こってしまうのは、介入割り当てに影響を及ぼす共変量すなわち交絡因子が存在する時であると説明しましたが、この交絡因子に関連する仮定を置くことにより、観察データからATEの推定に迫っていくことを考えます。その追加的な条件はUnconfoundednessと呼ばれ、ATEの推定に用いる観察データについて以下が成り立っていることを仮定します。

 (Y_i^{(1)}, Y_i^{(0)}) \perp W_i \; | \; X_i \quad \forall i = 1, ... , N

つまり、潜在的目的変数$(Y_i^{(1)}, Y_i^{(0)})$と介入割り当て$W_i$は、共変量$X_i$を条件付ければ独立であるということですが、「介入割り当ては共変量にのみ依存し、潜在的目的変数には依存しない」ということを要求しています。さらにこの条件は以下のように書き換えることができます。

E[ Y_i^{(k)} | W_i = 1, X_i ] = E[ Y_i^{(k)} | W_i = 0, X_i ] \quad \forall k \in \{0, 1\}

こちらの等式を元にこの仮定を解釈すると「同じ共変量を持つ人について、その人が実際に介入を受けた時の目的変数の期待値と、実際に介入を受けなかった時に仮に介入を受けたとした場合の目的変数の期待値が一致する（逆もまた然り）。」となります。と言いますか、それが成り立つような共変量が観測されていなければならないということです。このUnconfoundednessが成り立っているならば、前回の記事で紹介したSUTVAも同時に仮定することにより、

\begin{align}
& E \Bigl[ E\bigl[ Y_i^{obs} | W_i = 1, X_i \bigr] - E\bigl[ Y_i^{obs} | W_i = 0, X_i \bigr] \Bigr]   \\
& =  E \Bigl[ E\bigl[ Y_i^{(1)} | W_i = 1, X_i \bigr] - E\bigl[ Y_i^{(0)} | W_i = 0, X_i \bigr] \Bigr]
\quad \because SUTVA \\
& = E \Bigl[ E\bigl[ Y_i^{(1)} | X_i \bigr] - E\bigl[ Y_i^{(0)} | X_i \bigr] \Bigr] \quad \because Unconfoundedness \\
& = E \Bigl[ E\bigl[ Y_i^{(1)} -  Y_i^{(0)} | X_i \bigr] \Bigr] \\
& = E\bigl[ Y_i^{(1)} - Y_i^{(0)}  \bigr] \quad \because law \, of \, iterated \, expectation \\
& = ATE
\end{align}

が成り立ち、観察データからATEに迫ることができそうだとわかります。

この結果を用いたATEの推定方法として、回帰モデルを用いる方法・マッチング法・層別解析・ノンパラメトリック法などのATE推定方法が存在しますが、回帰モデルに関する仮定が非現実的であること、解析フローに恣意性が生じること、一定数のデータを捨てなければならないこと、次元の呪いの影響を大きく受けることなど、それぞれデメリットがあります。（詳しくは[2]の2章）そこで近年は、傾向スコアという概念を用いて交絡因子の影響を取り除く方法が多くの応用場面で用いられており、次章からはこの方法論についてまとめていきます。

傾向スコアによる交絡補正

ここでは、因果推論におけるとても重要な概念として知られている傾向スコアを用いて交絡因子による影響を取り除く方法について解説します。これはある共変量を持つデータが介入を受ける確率として以下のように定義されます。

e(x) = P(W_i = 1 | X_i = x) = E [W_i | X_i=x]

ただし、共変量空間における任意の点$x$において、$0<e(x)<1$を仮定します。つまり、データ中に絶対介入を受けるまたは受けないというデータが含まれていてはならないということです。ここで傾向スコアの便利な点はUnconfoundednessが成り立っているなら、わざわざ共変量で条件付けなくても傾向スコアで条件付けるだけで、介入割り当てと潜在的目的変数が統計的に独立になるという点です。この性質により、先ほど名前だけ紹介したマッチング法や層別解析など時には高次元に及ぶ共変量を用いて行なっていた部分の解析フローをたった1次元の傾向スコアに押し込めて代替することが出来るようになります。（しかしこの辺の細かい議論は記事が長くなってしまうので、また後日別記事にまとめます。）

さてここでは、導入した傾向スコアを用いるATE推定法の中でも代表的な推定方法の一つである「傾向スコアによる重み付け推定法（IPW推定法）」の紹介に焦点を絞ります。この方法では、以下の推定量によりATEを推定します。

E\Bigl[ \frac{W_i}{e(X_i)}Y^{obs} \Bigl] -  E\Bigl[ \frac{1-W_i}{1-e(X_i)}Y^{obs} \Bigl]

実は、このように構成される推定量は、Unconfoundednessの元でATEの不偏推定量であることが以下のように示されます。

\begin{align}
& E\Bigl[ \frac{W_i}{e(X_i)}Y_i^{obs} \Bigr] -  E\Bigl[ \frac{1-W_i}{1-e(X_i)}Y_i^{obs} \Bigr] \\
& = E\Bigl[ \frac{W_i}{e(X_i)}Y_i^{(1)} \Bigr] -  E\Bigl[ \frac{1-W_i}{1-e(X_i)}Y_i^{(0)} \Bigr] \quad \because SUTVA \\
& = E\Bigl[ E\bigl[ \frac{W_i}{e(X_i)}Y_i^{(1)} | X_i \bigr] \Bigr] -  E\Bigl[ E\bigl[ \frac{1-W_i}{1-e(X_i)}Y_i^{(0)} | X_i \bigl] \Bigr]  \quad \because law \, of \, iterated \, expectation \\
& = E\Bigl[ E\bigl[ \frac{W_i}{e(X_i)} | X_i \bigr] E\bigl[ Y_i^{(1)} | X_i \bigr] \Bigr] -  E\Bigl[ E\bigl[ \frac{1-W_i}{1-e(X_i)} | X_i \bigr] E\bigl[ Y_i^{(0)} | X_i \bigr] \Bigr]  \quad \because Unconfoundedness \\
& = E\Bigl[ E\bigl[ Y_i^{(1)} | X_i \bigr] \Bigr] -  E\Bigl[ E\bigl[ Y_i^{(0)} | X_i \bigr] \Bigr] \quad \because E[W_i | X_i] = e(X_i) \\
& = E\bigl[ Y_i^{(1)} - Y_i^{(0)} \bigr] \quad \because law \, of \, iterated \, expectation  \\
& = ATE
\end{align}

しかし観察データにおいて真の傾向スコアが分かっていることは稀であり、介入割り当てを共変量にロジスティック回帰等を用いて回帰することにより推定するというステップが実際は必要になります。そのような場合の傾向スコアの推定にバイアスが生じてしまっていたとしても、傾向スコアの一致推定量さえ得ることができれば、その傾向スコアの推定量を用いて計算されるIPW推定量もATEに対する一致推定量となります。

実データを用いた簡易実験

本章では、[4]で用いられている実データを使って前章で紹介したIPW推定法のフローを試し、[4]の解析結果の一部を再現してみます。解析の様子はこちらのノートブックをご覧ください。

用いたデータはスマホゲームアプリ運営会社A社のCMがA社のアプリ利用に対して有する因果効果を調査するために集められたデータです。今回の介入は「2014年12月1日~12月15日の間にA社のテレビCMを見たこと」と定義し、同12月16日〜12月31日における 1. アプリ利用率 2. アプリ利用回数 3.アプリ利用時間 に対する因果効果を推定します。使用データは観察データであり、介入群には4,144サンプルで統制群には5,856サンプルが含まれる計10,000サンプルの共変量、介入有無、3つの目的変数が記録されています。

今回のデータにおける交絡因子としては例えば年齢が考えられます。何故ならば、高齢者は日中も在宅している時間が長いと考えられるためCMによる介入を受けやすいと考えられる一方でスマホゲームアプリの利用率はそもそも高くないと考えられます。もちろん年齢以外にも交絡因子の存在は大いにあり得ますが、このような交絡の存在により今回のデータにおいて単純に目的変数の平均の差分を計算すると、ゲーム利用率はほぼ0、ゲーム利用回数とゲーム利用時間はそれぞれマイナスの値となり、CMには効果が無かったりむしろ逆効果であるという直感に反した結果が得られます。

ということで、前章で紹介した傾向スコアを用いたIPW推定法により、交絡因子による影響を補正した上で、それぞれの目的変数の増分を求めたところ、以下のようになりました。（ただし、今回Unconfoundednessのチェックは参考元にならい傾向スコア推定の当てはまりの良さであるAUCを計算することで、簡易に確認しています。）

目的変数	補正前ATE	補正後ATE	描画
アプリ利用率	+0.0022	+0.0323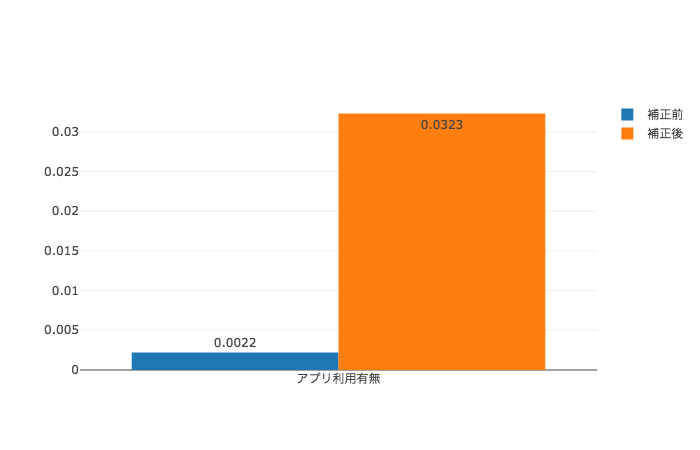
アプリ利用回数(回)	-1.485	+5.35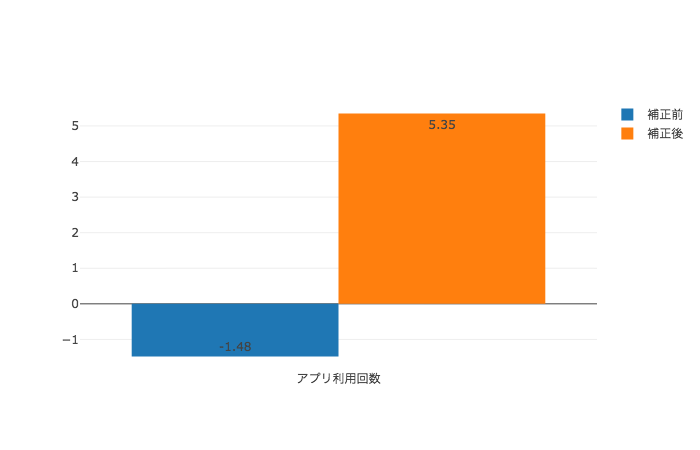
アプリ利用時間(秒)	-630	+1514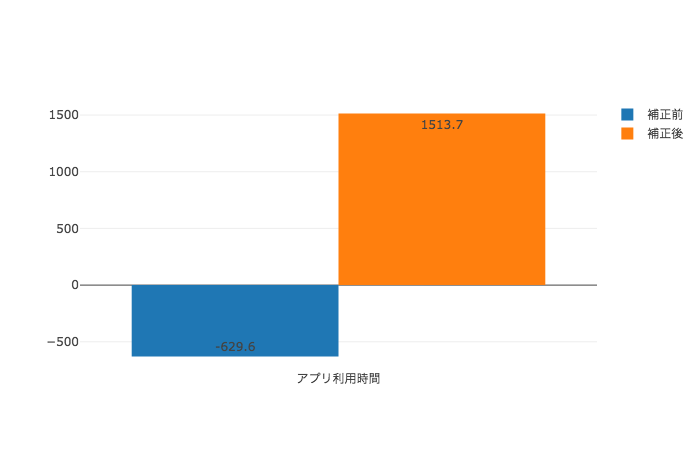

傾向スコアによる補正をかけたことで、全ての目的変数についてのATEがプラスであると推定されました。実際、[4]の解析結果では全ての目的変数のATEが5%有意水準で0より大きいという結果になったとされています。このように、傾向スコアを用いた交絡因子の補正を行うことにより、単純に計算した群間の平均値の差で推定した場合と逆の結論を導き出しています。（描画は、青が補正前でオレンジが補正後の推定値です。）

まとめ

今回は、A/Bテストを行うことができない状況で介入施策の効果をどのように推し量ることができるのか、その為に必要な仮定とはなんであるのかについて整理してみました。やはり、A/Bテストが可能な状況に比べて追加的な仮定（Unconfoundedness）が必要でありかつ、この仮定が成り立っていることを直接的に確認することができない以上、困難は大きいと思います。一方で、感度分析[1]などの方法論を用いることで結果の誤認識を極力廃す努力のもとで、現場に役立つ示唆を得ることは不可能ではありません。今後も因果推論の知識を蓄えることにより、非効率・非合理的な介入の減少に寄与することができないかと考えています。

次なる問題意識に向けてへ

2つの記事に渡ってある介入施策の因果効果を測定するための枠組みの解説をしてきました。これらの記事においてA/Bテストや傾向スコアを用いて目指していたのは、ATE（平均的因果効果）を推定することでした。そして、ATEが（有意に）正の値であることが確かめられたら、その介入施策を導入するという意思決定が自然かと思われます。しかし本当にこれで良いのでしょうか？

例えばある車の広告のATEが大きく正の値であることがA/Bテストを通じて明らかになったとします。しかしこれはあくまで実験の対象となった母集団に対しては平均的に因果効果が正であるというだけで、一人一人を見てみると例えば高齢で滅多に外出しない方など、広告の効果が全くないもしくは逆効果であるような個人が一定程度存在する可能性があります。つまり、因果効果にも異質性（heterogeneity）があると言うことですが、この個別的因果効果（ITE: Individual Treatment Effect）を予測することにより、因果効果の小さな人には介入しないといった個別化された最適な介入戦略を立てることが可能になります。

このような問題意識はUplift modelingと呼ばれる分野で取り扱われてきました。実は、このUplift modelingの基礎については以前記事にしているので興味がある方は是非ご一読ください。

参考

[1] G.Imbens, D.Rubin, Causal Inference for Statistics, Social and Biomedical Sciences. An Introduction, Cambridge University Press, 2015.
[2] 星野 崇宏, 調査観察データの統計科学, 岩波書店, 2009.
[3] https://www.krsk-phs.com/entry/counterfactual_assumptions
[4] 加藤諒, 星野 崇宏, 因果効果推定の応用 CM接触の因果効果と調整効果 岩波データサイエンスVol.3 岩波書店, 2016.