あなたはA/Bテストを理解しているか？

はじめに

A/Bテストは、ある介入施策の効果を測定するために多くの分野で一般的に用いられている方法です。例えば、医療においては「新薬がそれまで用いられていた薬よりも効果があると言えるのか？」だったり、インターネット広告においては「新広告レイアウトが旧広告レイアウトに比べて効果が大きいと言えるのか？」をA/Bテストで推し量ることができます。しかし、A/Bテストによる効果測定が当たり前になりすぎて、とりあえずA/Bテストを走らせよう！という盲目な意思決定に陥ってはいないでしょうか？今回の記事では、そもそもA/Bテストを走らせる意図からその原理に至るまでを自分なりに整理しつつ解説を試みます。

目次

1. はじめに
2. A/Bテストの目的
3. 因果の記述（Rubin Causal Model）
4. A/Bテストがやっていること
5. まとめ
6. 次なる問題意識に向けて
7. 参考

A/Bテストの目的

ここでは、A/Bテストを行う目的を簡単に整理します。「はじめに」でA/Bテストは、「ある介入施策の効果を測定するツール」であると言いました。ここでの「介入施策の効果」とは、一体何でしょうか？実は、ここで興味があるのは介入がもつ「因果効果」であると言えます。つまり介入によってどれだけの目的変数（コンバージョン率など）が見込めるのかではなくて、介入によってどれだけの目的変数の増加（または減少）が平均的に期待できるのかを測定することを目指します。これを今回は平均的因果効果(ATE: Average Treatment Effect) と呼びますが、以下のように定義できます。

ATE = (母集団全体が介入を受けた時の目的変数の平均) - (母集団全体が介入を受けなかった時の目的変数の平均)

この時、右辺の第1項と第2項の母集団について介入有無以外の要素が全て同じであるならば、これは介入の因果効果、つまり目的変数を平均的にどれくらい増加させたかの定義として妥当そうです。

しかし現実には、介入としてあるインターネット広告の配信を適用した時に、多くの人が商品を買ってくれたとしたらその広告に効果があったと考えてしまう（右辺第1項のみを考慮している）と思いますし、実際広告主にも大きな顔ができると思います。いわば広告配信後の目的変数が高くあって欲しいという指針で広告配信戦略などが決められることも実際のところ多いと思っていますが、A/Bテストは、「仮に広告配信していなかったとしても同じくらいの結果が得られたのではないか？」という仮説を検証することにより、達成された購入確率が、広告配信に起因するものであるのかを解き明かす（ATEを推定する）ための強力なツールとして現在の地位を築いています。

因果の記述（Rubin Causal Model）

前章で紹介したA/Bテストの目的であるATEですが、よくよく考えると計算不可能であることがわかります。何故ならば、介入有無以外の要素が全て同じである2つの集団を作り出すことはタイムマシンでもない限りどうやっても不可能だからです。つまり、介入を受けた群に対して、「もしも介入を受けなかったら...」といった仮想世界と現実に起こった世界の比較を行わないとATEに迫ることはできません。

実はそのような反実仮想に思いを巡らせるのに都合のいい考え方・因果の記述方法を1970年代にドナルド・ルービンという人が考え出していて、Rubin Causal Model(RCM)と呼ばれています。よってここでは、RCMの枠組みを紹介しつつ、ATEをきちんと定義していきます。ここの定式化を理解できると残りの話はすんなり腹落ちするはずです。まず今後は以下のNotationを用いることにします。

記号	意味
$i$	各データ
$X_i$	$i$の特徴量ベクトルを表す確率変数
$W_i$	データ$i$の介入有無を表す2値確率変数 ($W_i \in {0, 1}$)
$Y_i^{(1)}, Y_i^{(0)}$	それぞれ$W_i = 1, W_i = 0$で条件づけた時の$i$の目的変数の確率変数。「潜在的目的変数」
$Y_i^{obs}$	$i$について観測される目的変数（直後に詳しく）

さて、Notationを導入したところでRCMの枠組みを説明していきますが、RCMにおける最も重要な概念は「潜在的目的変数」だと言えるでしょう。通常の機械学習タスクでは基本的に、特徴量$X_i$から目的変数の期待値$E [Y_i | X_i]$を予測することが目的になることが多いと思います。当然この時、各データ$i$ごとに目的変数となる確率変数は唯一ですね。

しかし、先に導入したようにRCMでは、全てのデータは潜在的目的変数(potential outcomes)と呼ばれる目的変数の対$(Y_i^{(1)}, Y_i^{(0)})$を持っていると考えます。（今回は簡単のため介入は2種類であるとしていますが、一般的には介入の種類の数だけ各データが潜在的目的変数を持っていることを想定します。）この潜在的目的変数を用いることにより、ある介入が目的変数に対して有する因果効果（ATE）を以下のように定義することができます。

$$
ATE = E[Y_i^{(1)} - Y_i^{(0)}]
$$

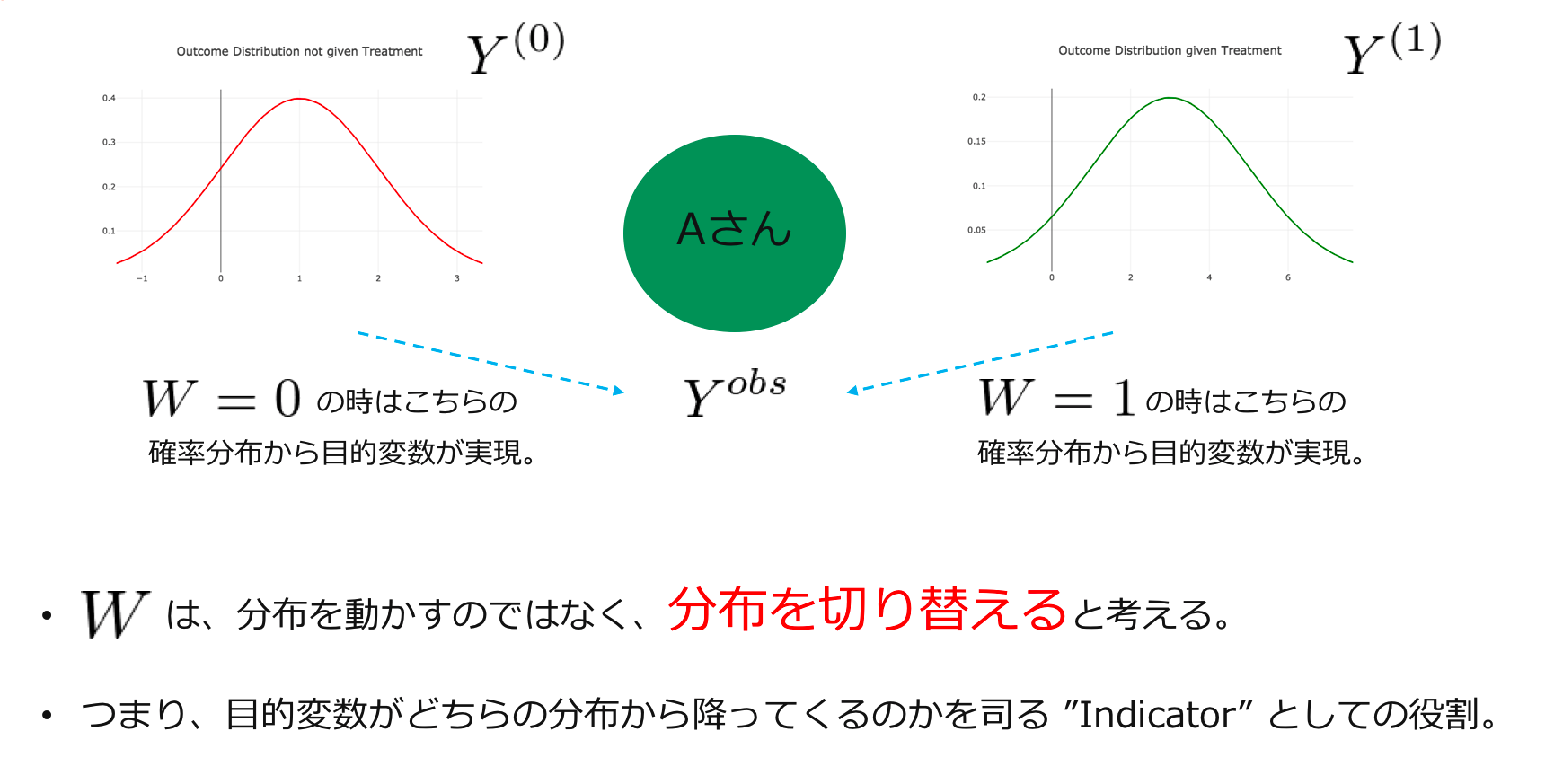
介入を受けた時の目的変数の母集団に対する期待値$E[Y_i^{(1)}]$と介入を受けなかった時の目的変数の母集団に対する期待値$E[Y_i^{(0)}]$ということです。ここで注意が必要なのは介入$W_i$の役割です。私は、因果推論を勉強し始めた時、ある介入の役割は「目的変数の確率分布自体を変化させること」だという先入観を無意識に抱いていて、その後の理解に苦しみました。（このような先入観を持つのは実は私だけなのかもしれませんが...）しかし、潜在的目的変数を導入したことにより、介入有無の役割は、目的変数の確率分布を動かすのではなく「切り替える」ことであると言うことができます。そして、複数の潜在的目的変数の分布の中から割り当てられた介入に対応する分布が選択されて、観測される目的変数が実現するというわけです。

よって、実際に観測される目的変数は以下のような確率変数$Y^{obs}$として表すことができます。潜在的目的変数のどちらが介入割り当て$W_i$によって選択される様子が読み取れるはずです。

$$ Y_i^{obs} = W_iY_i^{(1)} + (1 - W_i)Y_i^{(0)} $$

つまり、私たちが現実にアクセスできるのはこの$Y_i^{obs}$だけですが、これを用いてATEを推定する必要があります。それを可能にするのがA/Bテストだということです。一旦、ここまでの話を視覚的に図にまとめてみました。

A/Bテストがやっていること

A/Bテストの手順

A/Bテストが目指していることが整理できたところで、いよいよA/Bテストが介入の因果効果を推定するためのツールとして用いられる所以について触れていきます。
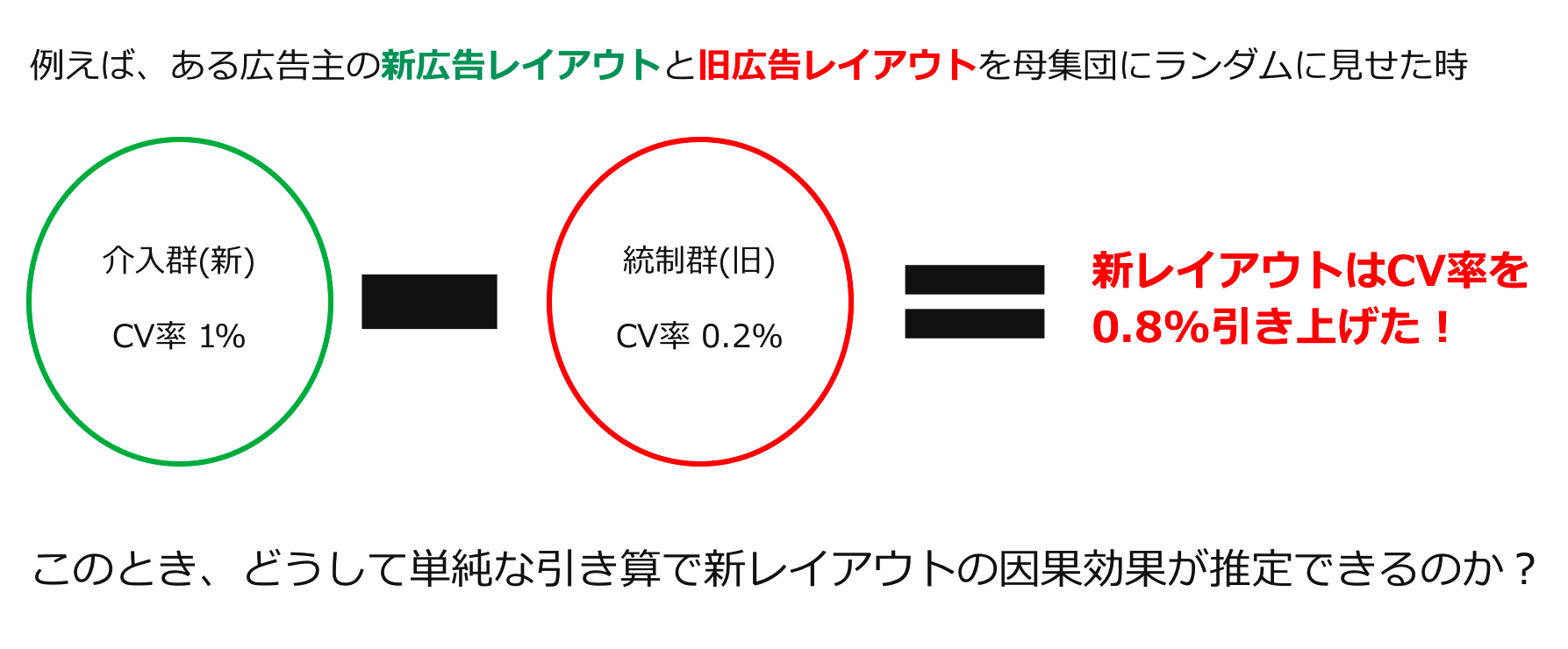
A/Bテストの手順は皆さんご存知の通り、被験者集団に対して効果を測定したい介入の割り当て有無をランダムに決めて、介入群と統制群を作った後にそれぞれの群の目的変数の平均の差分を見るというものです。（実際は、実現した差が統計的に有意であるか検定を行うことが多いと思います。）ここで以下のような簡単なA/Bテストの実行例を考えます。

さて、すでに図に記してしまっていますが、上の例の場合、新レイアウトによってCV率が0.8%引き上げられているから（ATEが大きいから）新レイアウトに移行しよう！という意思決定が自然かと思います。しかしどうして単純な引き算によって因果効果、つまりATEが推定できるのでしょうか？もう少し正確に表現すると、どうして以下の等式が成り立つと言えるのでしょうか？

$$
E[Y_i^{obs} | W_i = 1] - E[Y_i^{obs} | W_i = 0] = E[Y_i^{(1)} - Y_i^{(0)}]
$$

ここで、左辺は介入群と統制群の目的変数の期待値の差で、右辺が推定したいATEです。A/Bテストによる意思決定は往々にして重要になることが多いので、その背後に仮定している等式がなぜ成り立つのかを理解することは正しく結果を解釈するためにも重要であると言えます。

さて話を戻して問いに対する答えをこれから紐解いていきますが、上記の等式は「Mean Exchangeability」と「SUTVA」という性質が成り立っていれば示すことができます。

Mean Exchangeability

Mean Exchangeabilityは、A/Bテストが行う「ランダム割り当て」の末に実現する介入群と統制群に成り立つことが期待される性質です。この性質は、以下のように表されます。

$$
E [Y^{(k)} | W_i = 1] = E [Y^{(k)} | W_i = 0] \quad \forall k = 0,1
$$

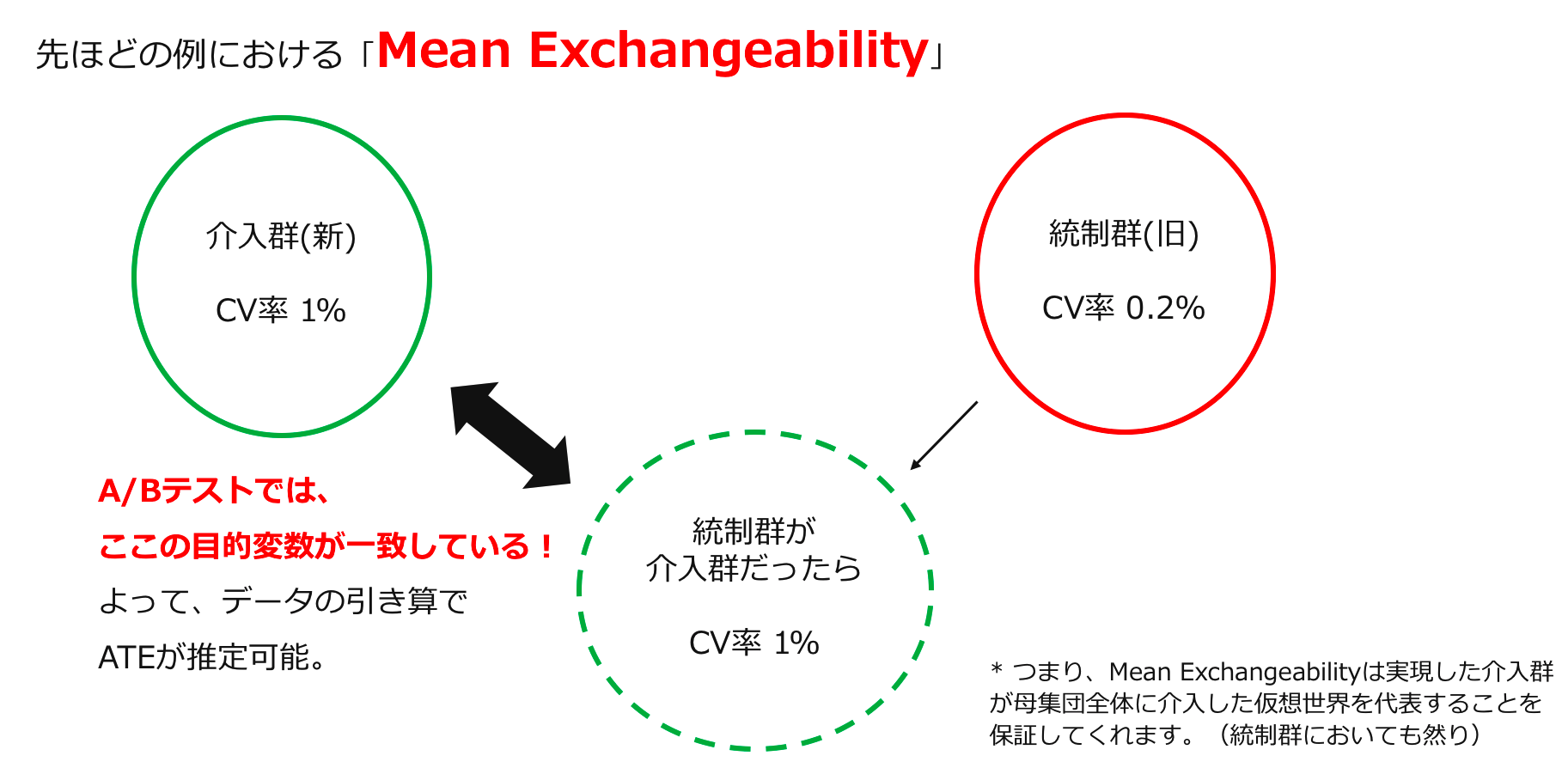
とまあ数式で表してみたものの、つまり何なの？という印象を持つ方が多いかと思います。上の数式を日本語に落とし込んでみると「実際に介入を受けた人たちの介入を受けた時の目的変数の期待値が、実際に介入を受けなかった人たちが仮に介入を受けた時の目的変数の期待値と一致することが期待される。」と言い表す事が出来ます。(これは、$k=1$の場合の説明ですが、$k=0$の時も同じように言い表せます。) この表現に、潜在的目的変数の考え方が色濃くにじみ出ていますが、先ほど図として掲載した例を用いて説明します。

まず、説明文の前半「実際に介入を受けた人たちの介入を受けた時の目的変数の期待値」ですが、これはバッチリ観測されていますね！そうです、介入群のCV率は1%でした。次に、後半部分である「実際に介入を受けなかった人たちが仮に介入を受けた時の目的変数の期待値」ですが、これは今統制群として観測されているCV率0.2%を持つ集団が、仮に介入を受けた場合、つまり、実際には$Y_i^{(0)}$から目的変数が実現しているところを$Y_i^{(1)}$から目的変数が実現すると仮定した場合の期待値ということになります。これは、どう頑張っても観測できません。なぜならば、あるデータに対して割り当てることができる介入種類はたかだか一種類だからです。しかしこれがなんとA/Bテストにより、今回の統制群が仮に介入群だった場合のCV率が1%である（実現した介入群のCV率）事が期待されます。以下に視覚的な説明も付しておきます。

注目に値するのはこの性質が仮定ではないという事です。A/Bテストにおけるランダムな介入割り当てが適切に行われているならば、このMean Exchangeabilityが成り立つ事が期待されるという事が、A/Bテストを強力なツールたらしめる一つの要因といえるでしょう。（注：確かにA/BテストはMean Exchangeabilityを成立させる事ができるという意味で強力ですが、あくまでこれは期待値での話です。実現した介入群と統制群においてこの性質が成り立っていると見做す事が出来るかを確かめるための検定の方法論も存在します（詳しくは[1]を参照）し、基本的にはある程度のサンプル数を集める事が必要になります。）

Stable Unit Treatment Value Assumption

しかし、これだけではまだA/Bテストによる意思決定が正当である事を保証する等式 $ E[Y_i^{obs} | W_i = 1] - E[Y_i^{obs} | W_i = 0] = E[Y_i^{(1)} - Y_i^{(0)}]$ を示すには不十分です。もう一つ次は仮定なのですが、Stable Unit Value Treatment Assumption (SUTVA)が成り立っていることが必要になります。これは次のような数式で表す事が出来ます。

$$
E[Y_i^{obs} | W_i=k] = E[Y_i^{(k)} | W_i = k] \quad \forall k=0,1
$$

これも日本語に落とし込んでみると「$k$という介入を受けた人から実現した目的変数の期待値は、その介入$k$と対応する潜在目的変数$Y^{(k)}$の期待値と一致していてくれ！」という仮定になります。この仮定が満たされないと考えられるのは次の2つの状況です。

(1) あるデータに対する介入割り当てが他のデータの目的変数にも影響を及ぼす。
(2) ある介入が（データの行動如何により）多段階存在しうる。

(1)の例

(1)はどういう事なのでしょうか。例えば、ある英語力向上プログラムが中学生の英語力向上（実験前後の試験で測定）に対する因果効果を有するか？を調べるためにA/Bテストを行うとします。この時、何も考えずにランダム割り当てをすると、同じクラスの中にプログラム受講者と非受講者が混在するような状況が考えられます。ここで、プログラム受講者のA君が飛躍的に英語力を伸ばしていることに感化されたプログラム非受講のB君も自力で英語の勉強に熱を入れ、事後の英語試験でとても良いの成績をとったとしましょう。この時、B君の成績はプログラム非受講時の目的変数である$Y^{(0)}$からの実現値だと言えるでしょうか？ちょっとこの仮定は強引な気がしますね。何故ならB君がいい成績をとったのは少なからずA君がプログラムを受講したことに影響を受けているからです。よってこのような状況は(1)に引っかかってしまいます。

こんな時は、母集団の定義を見直してみましょう。今まで考えていたのはプログラムの「中学生一人一人」に対する因果効果でした。そうしてしまったが故に学生間の相互作用（ピア効果）により(1)に抵触してしまいました。ではこれを「ある中学校」に対する因果効果を測定するというようにA/Bテストの目的を変更し、プログラムを学校単位で割り当てることにしましょう。すると学生間に比べて学校間の相互作用の影響はかなり小さいことから、プログラムがある中学校の英語力を平均的にどれくらい向上させるかを測定することができます。よって、(1)を避けるためには「母集団」を適切に設定することが必要であることがわかります。

(2)の例

次に(2)です。これは薬の例がわかりやすいと思います。頭痛に対するある薬の因果効果を測定したいときに、介入が「薬を1日5錠飲むこと」であると定義します。ただ実はこの薬がゲキマズで、介入群中の多くの人がズルをして1日2錠とか3錠とかしか飲んでいなかったとしましょう。このとき、介入群全員に「薬を1日5錠飲むこと」を指示していたとしても、実際には薬を何錠飲むかによって介入が多段階存在してしまっているという状況が発生しています。このような状況は、(2)に引っかかってしまうためSUTVAの仮定が満たされません。でもこのような状況の時、因果効果の推定は不可能なのでしょうか？

ここで(2)に引っかかってしまったのは介入の定義を「薬を1日5錠飲むこと」としていたからです。こんな時は介入の定義を見直して「薬を1日5錠飲むことを指示すること」にすれば役立つ結論を得ることができます。つまり、結果として誰が何錠服用しようが「薬を1日5錠飲むことを指示すること」はたかだか一段階の介入の定義ですので、(2)をクリアできます。さらに、実際に医師が患者に対してできる介入は「1日5錠飲ませる」ではなくて「1日5錠飲むことを指示する」ですので、後者の頭痛治癒に対する因果効果は実践上十分役に立つ情報と言えるでしょう。よって、(2)を避けるためには「介入」を適切に定義することが必要であることがわかります。

（余談：このような被験者の行動によって介入有無が変わってしまうような問題を扱う時のキーワードとして、「Non-compliance」とか「Instrumental Variable (IV)」とかがあります。気になる人は、Causal Inferenceというワードを添えて検索してみてください。）

証明

とまあ長々と説明してきましたが、Mean ExchangeabilityとSUTVAを合わせることにより、

\begin{align}
 & E[Y_i^{obs} | W_i = 1] - E[Y_i^{obs} | W_i = 0] \\ 
 & = E[Y_i^{(1)} | W_i = 1] - E[Y_i^{(0)} | W_i = 0] \quad \because SUTVA \\
 & = E[Y_i^{(1)} ] - E[Y_i^{(0)} ] \quad \because Mean \; Exchangeability \\
 & = E[Y_i^{(1)} - Y_i^{(0)}]
\end{align}

この章の冒頭の等式を導くことができました。つまり、A/Bテストによって

ATE = (母集団のうち介入を受けた群の目的変数の平均) - (母集団のうち介入を受けなかった群の目的変数の平均)

が成り立つので、現実に観測できる情報からATEを計算できるよ！ってなわけです。
普段何気なく使っているA/Bテストは、実は裏で不可能を可能にしていたんですね。

まとめ

今回の記事では、介入施策の効果測定の方法として一般に用いられるA/Bテストが何を推定しようとしているのか、そしてA/Bテストに基づく意思決定はなぜ、そしていつ正当性を持つのかについて整理してきました。
当たり前に用いられるほど強力なツールであるがゆえに雑に「とりあえずA/Bテストだ！」となるのではなくて、ランダム割り当てによって得られた2群にMean Exchangeabilityが成り立っているか、得られた結果が「どのような集団」において「どう定義された介入」に対して主張できる結果であるのかを（面倒ですが）丁寧に確認し、正確な解釈をすることが、誤解のない誠実な意思決定に繋がると信じています。

次なる問題意識に向けて

特に医療における介入効果測定の場面ではA/Bテストが行えないことが多々あります。例えば、喫煙が肺がんに及ぼしうる因果効果を知りたい時に、被験者に「1日に〇〇箱タバコを吸え！」と指示することは倫理的に難しいですし、そうでない場合も生身の人間を対象にする実験は、十分なサンプル数を確保するためのコストが膨大だったりします。このような状況においては、すでに何らかの割り当て基準により蓄積されたデータを用いてATEを推定することを目指します。しかし、このようなデータ（観察データ）は、A/Bテストで成り立っていた性質が成り立たないため、さらなる工夫や仮定が必要になります。この辺りの話題も別途まとめようと思っています。（9月11日追記：こちらにまとめました。）

参考

[1] G.Imbens, D.Rubin, Causal Inference for Statistics, Social and Biomedical Sciences. An Introduction, Cambridge University Press, 2015.
[2] 星野 崇宏, 調査観察データの統計科学, 岩波書店, 2009.
[3] https://www.krsk-phs.com/entry/counterfactual_assumptions