A/Bテストを多腕バンディット問題として解く方法（実装コード付き）

初めての投稿です

 以前からQiitaで記事を書いてみたいと思っていましたが、なかなか手が付けられずにいました。今回、大学院での研究を通じて多腕バンディット問題について学ぶ機会があり、これを題材に記事を書いてみようと思います。もし誤字や構成についてご意見・アドバイスがありましたら、ぜひお聞かせください。よろしくお願いいたします。

目次

1.はじめに
2.多腕バンディット問題とは
3.多腕バンディット問題を解くためのアルゴリズムの紹介
4.実装したソースコードと結果
5.おわりに

1. はじめに

 この記事を通して、多腕バンディット問題とは何かの簡単な説明をします。その後、多腕バンディット問題を解くためのアルゴリズムを2つほど紹介し、実装コードと実験結果を４章に記載したいと思います。 すでに多腕バンディット問題や多腕バンディット問題のA/Bテストに対する応用を知っている方は2, 3章をかっ飛ばしてください。

よくある疑問の解決

Q: A/Bテストって、複数の候補を一定回数均等に試してみて、データを収集すればいいのでは?(平等に試して、最終的な結果から一番良い候補選ぶべきじゃない??)

A: A/Bテストとして一番真っ当な手法であり、おっしゃる通りです。しかし、多腕バンディット問題について理解することで、もっと良い手法があることがわかります!

2. 多腕バンディット問題とは

 多腕バンディット問題とは、最終的な報酬(なんらかの評価)の最大化を目的として、複数の選択肢の中からどんな選択肢を逐次的に選ぶべきかを求める問題です。 最終的な報酬を最大化する という目的が強化学習と同じ点であり、強化学習という分類に属する問題です。

 今みなさんの目の前に、5つのスロットマシンがあるとします。１つ１つのそれぞれのスロットマシンの期待値や的中確率、的中した際の報酬(払い戻されるコインの量)は未知です。100回スロットマシンを動かして良いと言われた時に、最終的な報酬をどのように最大化しようと考えるでしょうか?!

1. 1つのスロットマシンあたり20回ずつ平等に動かす
2. 「スロットマシンをランダムに1つ選択して動かしてみる。的中したら再びそのスロットマシンを選択して動かす、外したら次のスロットマシンをランダムに選択する」 を繰り返す
3. 1つのスロットマシンあたり10回ずつ回してみて、最も報酬がもらえたスロットマシンを残り50回ひたすら回す

このように、良さそうな方法が思い浮かびそうですが、それと同時にどれも最適ではなさそうに思えます。この問題で難しいのは、一番良いスロットマシンを見つけながらも最終的な報酬を最大化したいというトレードオフです。
一番良いスロットマシンの探索に回数を重ねるほど、一番良いスロットマシンを動かすことのできる回数は減ってしまいます。一方で、少ない試行回数で一番良いスロットマシンを決めつけてしまうのも要注意です。実際は一番良いスロットマシンではなかったという確率が上がってしまいます。多腕バンディット問題はこのようなトレードオフを含んだ少々複雑な問題です。先ほどはスロットマシンの例をしましたが、多くの現実的な問題として考えることができます。
例えば、

1. 広告のクリック数を最大化したい(最もクリック率が高い広告を精度良く特定するために様々な種類の広告を掲載して見ないといけない中でも...)
2. 治療法の評価において、最も有用な治療法を迅速に特定したい(特定するためには何万人、何十万人という膨大な試行回数を重ねれば特定できるが、コストがかかってしまう。それ以上に 最も有用な治療法ではない治療法を受ける患者数を最小にしたい... )

などが挙げられます。"Aがいいかな? Bがいいかな? それともパターンCがいいかな?" などと一番良い種類を特定するためのテストを、A/Bテストと呼びます。この多腕バンディット問題に対する方法は、昔から研究し続けられているので、シンプルでかつ優秀なアルゴリズムについて次章で解説をしたいと思います。

3. アルゴリズムの簡単な紹介

　今回実装して見たのは、ε-greedy法と、Softmax法という手法(アルゴリズム)です。ページの最後に詳しく紹介されている他の方の素晴らしい解説記事を掲載させていただきますので、そちらをご覧ください。

ε-greedy法

• 1-εの確率で、今のところ最も良い(最も期待値の高い、あるいは...率が高い)選択肢を選ぶ
• 今のところ最も良い→ 実際に探索する中で得られた値ですので、暫定的に最良な選択肢と言って良いです。真の値が最も良いかは定かではありません。
• εの確率で、全選択肢の中から平等に選ぶ(選択肢が選ばれる確率は ε/K K:選択肢の個数)

Softmax法

• ソフトマックス関数を用いて、選択肢それぞれの選ばれる確率を設定する手法です。今のところの期待値、あるいは...率が高ければ高いほど、選択確率も高くなります。また、温度パラメータτが大きいほどランダム性が大きくなる仕様です。

4. 実装したソースコードと結果

　今回は3つの広告文の候補に関するA/Bテストを行いました。それぞれ真のクリック率が10, 20, 30%であるとして、10000人に送信してクリック数を比較して見たいとおもいます。３つの広告文を同じくらい送信すると、クリック数は2000件程度になりますが、3章で紹介した手法を使用した場合は果たしてどうなるのでしょうか。

import numpy as np
import matplotlib.pyplot as plt
# 広告のクリック率（仮に既知の値を設定します）
true_acceptance_rates = [0.1, 0.2, 0.3]  # 3つの広告文の真のクリック率

# エージェントのパラメータ
num_trials = 10000      # 試行回数
epsilon = 0.1          # 探索率 (10%の確率でランダムに選択)
temperature = 0.01

# 各アームの成功数と試行回数のカウンタ
success_counts = [0, 0, 0]
total_counts = [0, 0, 0]

success_counts_softmax = [0, 0, 0]
total_counts_softmax = [0, 0, 0]

# 各アームの平均クリック率を格納するリスト
average_acceptance_rates = [0, 0, 0]
average_acceptance_rates_softmax = np.zeros(3)

# 全アームに関する平均クリック率
total_average_acceptance_rates = []
total_average_acceptance_rates_softmax = []

# 広告文の選択と報酬の更新
for _ in range(num_trials):
    ######### Epsilon-Greedyによるアームの選択 ############
    if np.random.rand() < epsilon:
        chosen_arm = np.random.randint(0, 3)  # ランダムに選択
    else:
        chosen_arm = np.argmax(average_acceptance_rates)  # 現在の平均クリック率が最大のアームを選択
    # 実際のクリック結果をシミュレーション（確率に基づき、クリック/非クリックをランダム決定）
    acceptance = np.random.rand() < true_acceptance_rates[chosen_arm]
    
    ############ 各アームのスコアからソフトマックス確率を計算 ###########
    exp_scores = np.exp(average_acceptance_rates_softmax / temperature)
    probabilities = exp_scores / np.sum(exp_scores)
    # 確率に基づいてアームを選択
    chosen_arm_softmax = np.random.choice(len(true_acceptance_rates), p=probabilities)
    # 実際のクリック結果をシミュレーション（確率に基づき、クリック/非クリックをランダム決定）
    acceptance_softmax = np.random.rand() < true_acceptance_rates[chosen_arm_softmax]
    

    # 成功数と試行数の更新
    success_counts[chosen_arm] += int(acceptance)
    total_counts[chosen_arm] += 1
    success_counts_softmax[chosen_arm_softmax] += int(acceptance_softmax)
    total_counts_softmax[chosen_arm_softmax] += 1

    # 平均クリック率の更新
    average_acceptance_rates[chosen_arm] = success_counts[chosen_arm] / total_counts[chosen_arm]
    average_acceptance_rates_softmax[chosen_arm_softmax] = success_counts_softmax[chosen_arm_softmax] / total_counts_softmax[chosen_arm_softmax]
    total_average_acceptance_rates.append(sum(success_counts)/sum(total_counts))
    total_average_acceptance_rates_softmax.append(sum(success_counts_softmax)/sum(total_counts_softmax))
    
# 結果の表示
for i in range(3):
    print(f"広告文 {i + 1}:")
    print(f"  - 実際のクリック率: {true_acceptance_rates[i]:.2f}")
    print(f"  - 推定クリック率: {average_acceptance_rates[i]:.2f}")
    print(f"  - 試行回数: {total_counts[i]}")

print(f"\n広告全体の合計クリック数: {sum(success_counts)}")

# グラフを描画
plt.plot(np.arange(10000), total_average_acceptance_rates, label=f"ε-greedy ε={epsilon}")
plt.plot(np.arange(10000), total_average_acceptance_rates_softmax, label=f"softmax τ={temperature}")
plt.xlabel("Trials")
plt.ylabel("Acceptance Rate")
plt.title("Average Acceptance Rate Over Time")
plt.legend()
plt.grid()
plt.savefig('Average_Acceptance_Rate.png')  # PNG形式で保存
plt.show()

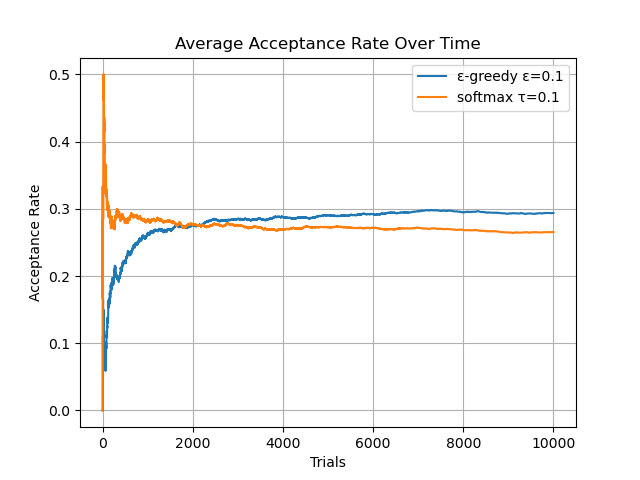
結果は以下のようになりました。平等に３つの広告文を送信すると2000件程度(20%)になりますが、どちらも大幅に上回る26-29%程度になりました。実際にε-greedy法ではクリック数が2938という結果になりました。簡単なアルゴリズムでもかなり優秀なことがわかりました。

5. おわりに

もう少し多腕バンディット問題について深く学んで、コンテクスチュアル多腕バンディット問題についての実装に関する記事も書いて見たいなと思います。

詳しくてわかりやすい解説記事: https://qiita.com/tsugar/items/b809f8d6399cc988aa69
詳しくてわかりやすい解説記事: https://qiita.com/pocokhc/items/fd133053fa309bdb58e6
詳しくてわかりやすい解説記事: https://qiita.com/usaito/items/ad15394547bd5daf8937