概要
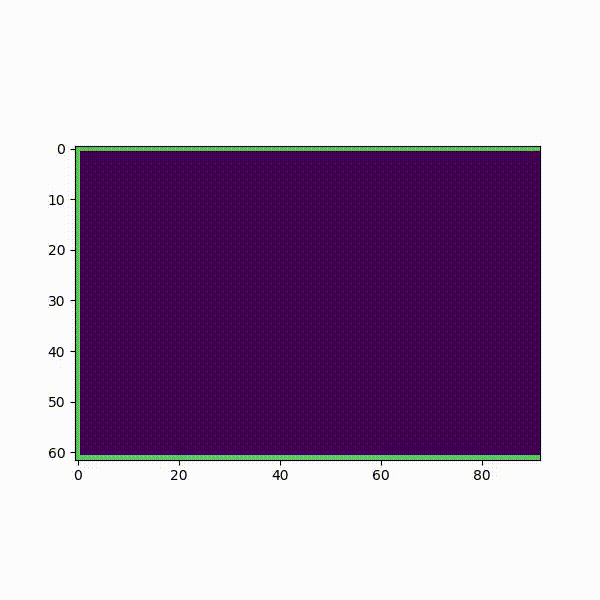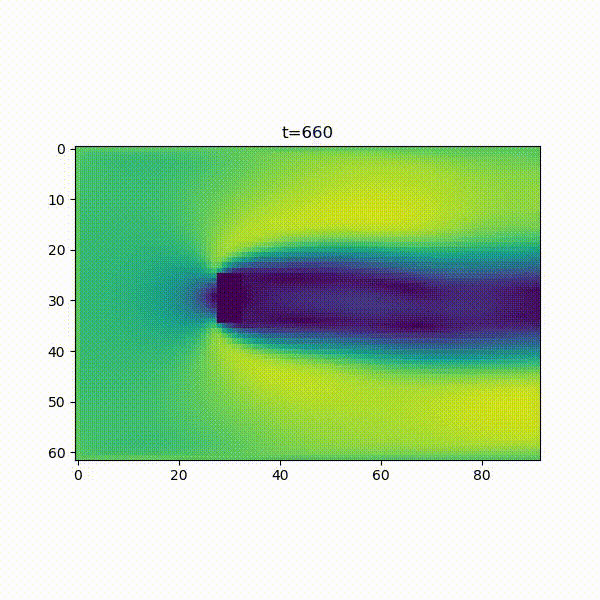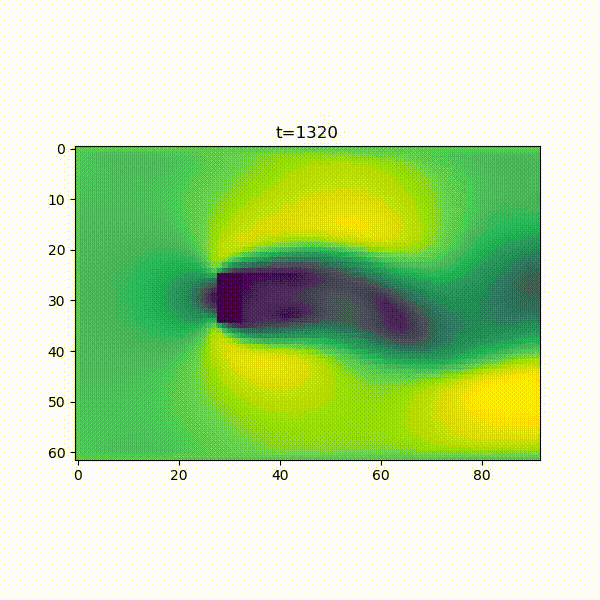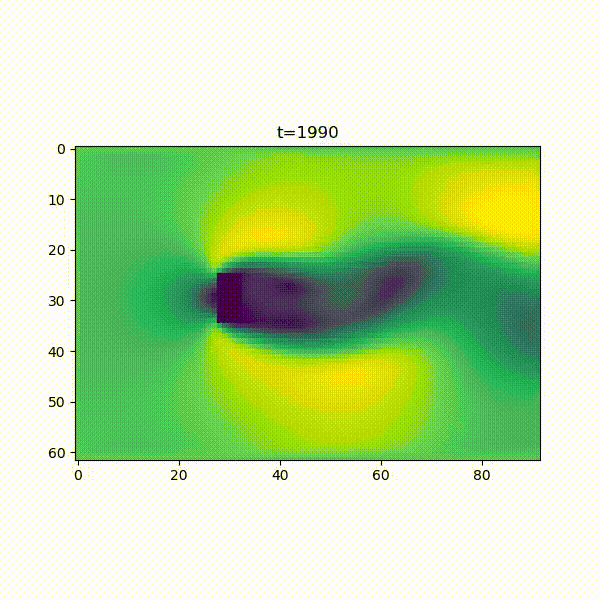
非圧縮性のナビエストークス方程式を解き、流体シミュレーションでカルマン渦を作成します。目標は、以下のようなカルマン渦の作成。ここに折りたたんでいるpythonコードを実行すると、2、 3分ほどで以下のようなカルマン渦シミュレーションができます。
pythonコード
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import scipy.sparse
from sksparse.cholmod import cholesky
def ConvectionTerm(u, v, flag_v, u_old, v_old):
for i in range(1, num_vy-1):
for j in range(1, num_vx-1):
if flag_v[i, j] >= 1: continue
if u_old[i, j] >= 0 and v_old[i, j] >= 0:
u[i, j] -= (u_old[i, j] * (u_old[i, j] - u_old[i, j-1]) + v_old[i, j] * (u_old[i, j] - u_old[i-1, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j] - v_old[i, j-1]) + v_old[i, j] * (v_old[i, j] - v_old[i-1, j])) * delta_t / delta
elif u_old[i, j] < 0 and v_old[i, j] >= 0:
u[i, j] -= (u_old[i, j] * (u_old[i, j+1] - u_old[i, j]) + v_old[i, j] * (u_old[i, j] - u_old[i-1, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j+1] - v_old[i, j]) + v_old[i, j] * (v_old[i, j] - v_old[i-1, j])) * delta_t / delta
elif u_old[i, j] >= 0 and v_old[i, j] < 0:
u[i, j] -= (u_old[i, j] * (u_old[i, j] - u_old[i, j-1]) + v_old[i, j] * (u_old[i+1, j] - u_old[i, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j] - v_old[i, j-1]) + v_old[i, j] * (v_old[i+1, j] - v_old[i, j])) * delta_t / delta
else:
u[i, j] -= (u_old[i, j] * (u_old[i, j+1] - u_old[i, j]) + v_old[i, j] * (u_old[i+1, j] - u_old[i, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j+1] - v_old[i, j]) + v_old[i, j] * (v_old[i+1, j] - v_old[i, j])) * delta_t / delta
return
def DiffusionTerm(v, v_old, flag_v):
for i in range(1, num_vy-1):
for j in range(1, num_vx-1):
if flag_v[i, j] >= 1: continue
v[i, j] += (v_old[i+1, j] + v_old[i-1, j] + v_old[i, j+1] + v_old[i, j-1] - 4*v_old[i, j]) * delta_t / (delta**2 * Re)
return
def DiverV(s, u, v, flag_v):
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_v[i, j] >= 3 or flag_v[i-1, j] >= 3 or flag_v[i-1, j-1] >= 3 or flag_v[i, j-1] >= 3:
continue
if flag_v[i, j] == 2:
if i == num_py-2: u[i, j], v[i, j] = u[i-1, j], v[i-1, j]
else: u[i, j], v[i, j] = u[i, j-1], v[i, j-1]
if flag_v[i-1, j] == 2:
if i-1 == 0: u[i-1, j], v[i-1, j] = u[i, j], v[i, j]
else: u[i-1, j], v[i-1, j] = u[i-1, j-1], v[i-1, j-1]
if flag_v[i, j-1] == 2:
if i == num_py-2: u[i, j-1], v[i, j-1] = u[i-1, j-1], v[i-1, j-1]
else: u[i, j-1], v[i, j-1] = u[i, j], v[i, j]
if flag_v[i-1, j-1] == 2:
if i-1 == 0: u[i-1, j-1], v[i-1, j-1] = u[i, j-1], v[i, j-1]
else: u[i-1, j-1], v[i-1, j-1] = u[i-1, j], v[i-1, j]
s[i, j] = (
u[i-1, j] - u[i-1, j-1] + u[i, j] - u[i, j-1] + \
v[i, j-1] - v[i-1, j-1] + v[i, j] - v[i-1, j]
) * delta / (2*delta_t)
return
def Cholesky(p, s, flag_p, factor):
s = s[1:-1, 1:-1] * -1
b = s.reshape((-1,))
x = factor(b)
x = x.reshape((num_Ay, num_Ax))
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_p[i, j] >= 1: continue
p[i, j] = x[i-1, j-1]
if flag_p[i+1, j] == 2: p[i+1, j] = x[i-1, j-1]
if flag_p[i-1, j] == 2: p[i-1, j] = x[i-1, j-1]
if flag_p[i, j+1] == 2: p[i, j+1] = x[i-1, j-1]
if flag_p[i, j-1] == 2: p[i, j-1] = x[i-1, j-1]
return
def PressureTerm(p, u, v, flag_p, flag_v, factor):
s = np.zeros((num_py, num_px))
DiverV(s, u, v, flag_v)
Cholesky(p, s, flag_p, factor)
return
def UpdateV(u, v, p, flag_v):
for i in range(1, num_vy-1):
for j in range(1, num_vx-1):
if flag_v[i, j] >= 1: continue
u[i, j] -= (p[i, j+1] - p[i, j] + p[i+1, j+1] - p[i+1, j]) * delta_t / (2*delta)
v[i, j] -= (p[i+1, j] - p[i, j] + p[i+1, j+1] - p[i, j+1]) * delta_t / (2*delta)
return
def NablaV(u, v, flag_v):
nablav = 0
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_v[i, j] >= 3: continue
elif flag_v[i-1, j] >= 3: continue
elif flag_v[i-1, j-1] >= 3: continue
elif flag_v[i, j-1] >= 3: continue
nablav += u[i-1, j] - u[i-1, j-1] + u[i, j] - u[i, j-1] + \
v[i, j-1] - v[i-1, j-1] + v[i, j] - v[i-1, j]
return nablav
def initA(flag_p):
N = num_Ax * num_Ay
A = np.eye(N) * 4
for i in range(N):
if flag_p[i // num_Ax + 1, i % num_Ax + 1] >= 2:
A[i, i] = 1
continue
Apij = [
[i, i-num_Ax, i // num_Ax, i % num_Ax + 1],
[i, i-1, i // num_Ax + 1, i % num_Ax],
[i, i+1, i // num_Ax + 1, i% num_Ax + 2],
[i, i+num_Ax, i // num_Ax + 2, i % num_Ax + 1]
]
for Ai, Aj, pi, pj in Apij:
if flag_p[pi, pj] == 2:
A[Ai, Ai] -= 1
if Aj < 0 or Aj >= N:
continue
if flag_p[pi, pj] >= 1 or pi == 0 or pi == num_py-1 \
or pj == 0 or pj == num_px-1:
A[Ai, Aj] = 0
else:
A[Ai, Aj] = -1
A = scipy.sparse.csc_matrix(A)
return A
# define
num_gridx = 90
num_gridy = 60
delta = 0.1
delta_t = 0.05
u_value = 0.98
v_value = 0.02
object_sizex = 5
object_sizey = 10
object_posix = 30
object_posiy = 30
Re = 100
time_step = 2000
plot_interbal = 10
object_startx = object_posix - object_sizex // 2 + 1
object_endx = object_startx + object_sizex
object_starty = object_posiy - object_sizey // 2 + 1
object_endy = object_starty + object_sizey
num_vx = num_gridx+2
num_vy = num_gridy+2
num_px = num_vx+1
num_py = num_vy+1
num_Ax, num_Ay = num_px-2, num_py-2
def main():
#init boundary
#u, v, p
u = np.zeros((num_vy, num_vx))
u[0,:], u[:,0], u[-1,:] = u_value, u_value, u_value
v = np.zeros((num_vy, num_vx))
v[0,:], v[:,0], v[-1,:] = v_value, v_value, v_value
p = np.zeros((num_py, num_px))
#flag_v, flag_p
flag_v = np.zeros((num_vy, num_vx))
flag_v[:, -1] = 2
flag_v[0, :], flag_v[-1, :], flag_v[:, 0] = 1, 1, 1
flag_p = np.zeros((num_py, num_px))
flag_p[:, -1] = 2
flag_p[0, :], flag_p[-1:, :], flag_p[:, 0] = 1, 1, 1
#init object
#u, v, p
#flag_v, flag_p
flag_v[object_starty:object_endy, object_startx:object_endx] = 1
flag_v[object_starty+1:object_endy-1, object_startx+1:object_endx-1] = 3
flag_p[object_starty+1:object_endy, object_startx+1:object_endx] = 2
flag_p[object_starty+2:object_endy-1, object_startx+2:object_endx-1] = 3
#create A
A = initA(flag_p)
factor = cholesky(A)
print(f"t=0 divergence v: {NablaV(u, v, flag_v)}")
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111)
img = ax.imshow(np.sqrt(u*u + v*v), vmin=0, vmax=1.3, cmap="viridis")
ax.set_title(f"t=0")
def run_simulate(t):
u_old = u.copy()
v_old = v.copy()
ConvectionTerm(u, v, flag_v, u_old, v_old)
DiffusionTerm(u, u_old, flag_v)
DiffusionTerm(v, v_old, flag_v)
PressureTerm(p, u, v, flag_p, flag_v, factor)
UpdateV(u, v, p, flag_v)
if (t+1) % plot_interbal == 0:
print(f"t={t+1} divergence v: {NablaV(u, v, flag_v)}")
normv = np.sqrt(u*u + v*v)
plt.cla()
img = ax.imshow(np.sqrt(u*u + v*v), vmin=0, vmax=1.3, cmap="viridis")
ax.set_title(f"t={t+1}")
ani = animation.FuncAnimation(fig, run_simulate, interval=1, frames=time_step, repeat=False)
#ani.save("out.mp4", writer="ffmpeg")
plt.show()
if __name__ == '__main__':
main()
流体シミュレーションでは圧力の計算に時間がかかる。そこで本記事では、Poisson方程式をコレスキー分解で解く。Poisson方程式を解く方法は以下の通り(他にもたくさんあると思います。。。)
- 行列を新たに作成しない方法 : Jacobi法、Gauss-Seidel法、SOR法
- 行列を新たに作成する必要がないので、コードを書くのが楽
- 収束に時間がかかってしまい、計算する格子数、時間ステップ数が多くなると計算コストが大きくなる
- 行列を新たに作成する方法 : 反復法(CG法、、、)、直接法(Cholesky分解、、、)
- 行列を新たに作成する必要があるので、コードを書くのが面倒
- 解くべき行列が正定値対称行列なため、CG法やCholesky分解が使える
- 計算コストが小さい
カルマン渦を作成するためには、ある程度の格子数、時間ステップ数が必要となるため、SOR法よりも、CG法、Cholesky分解の方が30倍ほど早い。速度比較について詳しくは補足1。
流体中に物体のあるシミュレーションで、行列を使ってPoisson方程式を解く方法を調べても、あまり記事が見つからなかったので、本記事ではそこの解説に重点をおく。
対象読者
- pythonでサクッとカルマン渦をシミュレーションしたい人
- 流体中に物体があるシミュレーションで、行列を使ってPoisson方程式を解く方法を知りたい人
環境
macOS Mojave: 10.14.6
python: 3.7.4
numpy: 1.19.0
matplotlib: 3.2.2
scipy: 1.3.1
sksparse: 0.4.4
シミュレーションの条件
- Fractional Step法
- 格子モデル : Arakawa-B型スタッガード格子
- 移流項(対流項) : 一次精度風上差分法
- 拡散項(粘性項) : 中心差分法
- 圧力(Poisson方程式)の計算 : コレスキー分解
基本的にはこちらの東工大の記事を基にコードを書いた。上記のうち、Poisson方程式をコレスキー分解で解くこと以外は東工大の記事と同じである。こちらの記事「仮眠プログラマーのつぶやき 流体力学のプログラムを作りたい!その1」ではArakawa-C型スタッガード格子ではあるが、非常にわかりやすく参考になった。
非圧縮性のNavier-Stokes方程式
非圧縮性のNavier-Stokes方程式の概要については、こちらの記事「【Python】流体シミュレーション : 非圧縮性 Navier-Stokes 方程式」が参考になった。
非圧縮性のNavier-Stokes方程式
\frac{\partial \vec{v}}{\partial t} =- (\vec{v} \cdot \nabla)\vec{v} - \nabla p + \frac{1}{Re} \nabla^2 \vec{v} \\
(\vec{v} \cdot \nabla)\vec{v} : \text{移流項} \\
- \nabla p : 圧力項 \\
\frac{1}{Re} \nabla^2 \vec{v} : \text{拡散項} \\
連続の式
$$
\nabla \cdot \vec{v} = 0
$$
Fractional Step法
非圧縮性のNavier-Stokes方程式を解く有名な方法にSMAC法もあるが、Fractional Step法の方が解析が安定しており、カルマン渦が実験結果とも近い「変数をコロケート配置した場合の SMAC 法と部分段階法の結果の違い」ということで、本記事ではFractional Step法を採用する。Fractional Step法については、こちらの記事「数学とか語学とか楽しいよね 【Navier-Stokes方程式】フラクショナルステップ法によるNavier-Stokes方程式の離散化」が非常にわかりやすく助かりました。結論から書くと、Fractional Step法は以下の手順で計算を進めていく。
-
速度$\vec{v}^{n}$から移流項、拡散項を計算し、仮の速度$\vec{v}'$を求める
$$
\vec{v}' = \vec{v}^n - \Delta t (\vec{v}^{n} \cdot \nabla)\vec{v}^n + \frac{\Delta t}{Re} \nabla^2 \vec{v}^n
$$ -
仮の速度$\vec{v}'$を使って、圧力$p^{n+1}$を求める
$$
\nabla^2 p^{n+1} = \nabla \vec{v}' / \Delta t
$$ -
圧力$p^{n+1}$から$\vec{v}^{n+1}$を求める
$$
\vec{v}^{n+1} = \vec{v}' - \nabla p^{n+1}
$$
Arakawa-B型スタッガード格子
Arakawa-B型スタッガード格子については、東工大の記事のこちらが非常にわかりやすいです。Arakawa-B型スタッガード格子は物体の境界条件を考えやすい。他にはコロケート格子、Arakawa-C型スタッガード格子がある。
境界条件
本記事での境界条件は大きく4つある(流入、流出、物体表面、物体内部)。以後、速度の$x, y$成分をそれぞれ$u, v$とする。
| 境界の種類 | 速度 | 圧力 |
|---|---|---|
| 流入条件 | $u=1$で一定 | 0で一定 |
| 流出条件 | $\frac{\partial v}{\partial x} = 0$ | $\frac{\partial p}{\partial x} = 0$ |
| 物体表面 | 0で一定 | $\frac{\partial p}{\partial x} = 0, \frac{\partial p}{\partial y} =0$ |
| 物体内部 | 0で一定 | 0で一定 |
物体の境界条件については、こちらの東工大の記事がわかりやすい。流入条件の速度については$u=1$としているが、$u=0.98, v = 0.02$とした方が、カルマン渦が発生しやすい。
コードを書くときには、境界条件を一括で管理するためにflag_v、flag_pという配列を用意する。この配列の値は、境界条件に応じて次のように定める
- 速度または圧力の参照も更新もする : 0 (ex 流体のセル
- 速度または圧力の参照はするが、更新はせず一定に保つ : 1 (ex 流入、物体表面
- 速度または圧力の参照をするときに、位置の微分 = 0を満たすように変更する : 2 (ex 流出、物体表面
- 速度または圧力の参照も更新もしない : 3 (ex 物体の内部
| 境界の種類 | 速度 | flag_vの値 | 圧力 | flag_pの値 |
|---|---|---|---|---|
| 流入条件 | $u=1$で一定 | 1 | 0で一定 | 1 |
| 流出条件 | $\frac{\partial v}{\partial x} = 0$ | 2 | $\frac{\partial p}{\partial x} = 0$ | 2 |
| 物体表面 | 0で一定 | 1 | $\frac{\partial p}{\partial x} = 0, \frac{\partial p}{\partial y} =0$ | 2 |
| 物体内部 | 0で一定 | 3 | 0で一定 | 3 |
1. 移流項、拡散項を計算し、仮の速度を求める
$$
\vec{v}' = \vec{v}^n - \Delta t (\vec{v}^{n} \cdot \nabla)\vec{v}^n + \frac{\Delta t}{Re} \nabla^2 \vec{v}^n
$$
成分ごとに分けると
$$
u' = u - \Delta t \left( u \frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} \right) + \frac{\Delta t}{Re} \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right)
$$
$$
v' = v - \Delta t \left( u \frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} \right) + \frac{\Delta t}{Re} \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} \right)
$$
移流項を一次精度風上差分法で計算する
一次精度風上差分法については、こちらの記事「差分法の基礎 一次精度風上差分法」が非常にわかりやすい。速度の方向によって計算方法が変わるので、コードが少しめんどくさい。また、$i, j$がそれぞれ$y, x$に対応していることに注意。計算すべき式は以下の通り。以後$\Delta x = \Delta y = \delta$とする。
$u \geq 0 \quad and \quad v \geq 0$のとき
$$
\left( u \frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} \right) = \frac{u}{\delta} (u_{i,j} - u_{i,j-1}) + \frac{v}{\delta} (u_{i,j} - u_{i-1,j})
$$
$$
\left( u \frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} \right) = \frac{u}{\delta} (v_{i,j} - v_{i,j-1}) + \frac{v}{\delta} (v_{i,j} - v_{i-1,j})
$$
$u \geq 0 \quad and \quad v \lt 0$のとき ...以下コード参照
$u \lt 0 \quad and \quad v \geq 0$のとき ...以下コード参照
$u \lt 0 \quad and \quad v \lt 0$のとき ...以下コード参照
def ConvectionTerm(u, v, flag_v, u_old, v_old):
for i in range(1, num_vy-1):
for j in range(1, num_vx-1):
if flag_v[i, j] >= 1: continue
if u_old[i, j] >= 0 and v_old[i, j] >= 0:
u[i, j] -= (u_old[i, j] * (u_old[i, j] - u_old[i, j-1]) + v_old[i, j] * (u_old[i, j] - u_old[i-1, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j] - v_old[i, j-1]) + v_old[i, j] * (v_old[i, j] - v_old[i-1, j])) * delta_t / delta
elif u_old[i, j] < 0 and v_old[i, j] >= 0:
u[i, j] -= (u_old[i, j] * (u_old[i, j+1] - u_old[i, j]) + v_old[i, j] * (u_old[i, j] - u_old[i-1, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j+1] - v_old[i, j]) + v_old[i, j] * (v_old[i, j] - v_old[i-1, j])) * delta_t / delta
elif u_old[i, j] >= 0 and v_old[i, j] < 0:
u[i, j] -= (u_old[i, j] * (u_old[i, j] - u_old[i, j-1]) + v_old[i, j] * (u_old[i+1, j] - u_old[i, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j] - v_old[i, j-1]) + v_old[i, j] * (v_old[i+1, j] - v_old[i, j])) * delta_t / delta
else:
u[i, j] -= (u_old[i, j] * (u_old[i, j+1] - u_old[i, j]) + v_old[i, j] * (u_old[i+1, j] - u_old[i, j])) * delta_t / delta
v[i, j] -= (u_old[i, j] * (v_old[i, j+1] - v_old[i, j]) + v_old[i, j] * (v_old[i+1, j] - v_old[i, j])) * delta_t / delta
return
拡散項を中心差分法で計算する
計算すべき式は以下の通り。
$$
\left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) = \frac{u_{i+1,j} + u_{i-1,j} + u_{i,j+1} + u_{i,j-1} - 4u_{i,j}}{\delta^2}
$$
$$
\left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} \right) = \frac{v_{i+1,j} + v_{i-1,j} + v_{i,j+1} + v_{i,j-1} - 4v_{i,j}}{\delta^2}
$$
$u, v$成分が同じ形となっているので、関数を使い回す。
def DiffusionTerm(v, v_old, flag_v):
for i in range(1, num_vy-1):
for j in range(1, num_vx-1):
if flag_v[i, j] >= 1: continue
v[i, j] += (v_old[i+1, j] + v_old[i-1, j] + v_old[i, j+1] + v_old[i, j-1] - 4*v_old[i, j]) * delta_t / (delta**2 * Re)
return
2. 仮の速度を使って、圧力を求める
以下のPoisson方程式を解いて圧力を求める
$$
\nabla^2 p^{n+1} = \nabla \vec{v}' / \Delta t
$$
離散化すると
$$
\nabla^2 p = - 4p_{i,j} + p_{i+1,j} + p_{i-1,j} + p_{i,j+1} + p_{i,j-1}
$$
$$
\nabla \vec{v}' = \frac{1}{2 \delta} ( u_{i-1,j} - u_{i-1,j-1} + u_{i,j} - u_{i,j-1} + v_{i,j-1} - v_{i-1,j-1} + v_{i,j} - v_{i-1,j} )
$$
Poisson方程式を行列を使って計算する
Poisson方程式の左辺を離散化し、右辺を$s$、両辺に-1をかけると
$$
4p_{i,j} - p_{i+1,j} - p_{i-1,j} - p_{i,j+1} - p_{i,j-1} = - s_{i,j}
$$
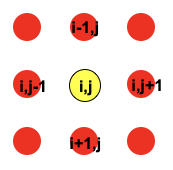
上記の式左辺は以下のように図形的に考えると、中心の圧力を4倍したものから周りの圧力の値を引けばいいことがわかる。
物体が存在しない場合の行列の作成
行列を作成する上でめんどうなのが、境界条件flag_p = 2のとき、つまり値の参照をするときに、位置の微分 = 0を満たすように値を変更するときである(物体の表面や流入)。この条件がめんどうなので、まずは物体がなく境界条件が全てflag_p = 1のときの簡単な例からみていく。
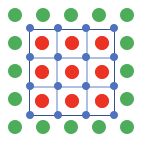
グリッド数 : 4x4
速度の数 : 4x4 青丸
圧力の数 : 5x5 赤丸、緑丸
緑丸は境界条件flag_p = 1であり、$p=0$で一定のままである
この条件でのPoisson方程式の行列表現は、以下のように規則的できれいな行列になる。
\left[
\begin{array}{c}
4 & -1 & 0 & -1 & 0 & & \cdots & & 0 \\
-1 & 4 & -1 & 0 & -1 & 0 & & & \\
0 & -1 & 4 & 0 & 0 & -1 & 0 & & \vdots \\
-1 & 0 & 0 & 4 & -1 & 0 & -1 & 0 & \\
0 & -1 & 0 & -1 & 4 & -1 & 0 & -1 & 0 \\
& 0 & -1 & 0 & -1 & 4 & 0 & 0 & -1 \\
\vdots & & 0 & -1 & 0 & 0 & 4 & -1 & 0 \\
& & & 0 & -1 & 0 & -1 & 4 & -1 \\
0 & & \cdots & & 0 & -1 & 0 & -1 & 4 \\
\end{array}
\right]
\left[
\begin{array}{c}
p_{11} \\
p_{12} \\
p_{13} \\
p_{21} \\
p_{22} \\
p_{23} \\
p_{31} \\
p_{32} \\
p_{33} \\
\end{array}
\right] = -
\left[
\begin{array}{c}
s_{11} \\
s_{12} \\
s_{13} \\
s_{21} \\
s_{22} \\
s_{23} \\
s_{31} \\
s_{32} \\
s_{33} \\
\end{array}
\right]
実際に展開してみると、Poisson方程式が満たされていることがわかる。次からが本題である。
物体が存在する場合の行列の作成
物体の表面
物体の表面ではflag_p = 2つまり値の参照をするときに、位置の微分 = 0を満たすように値を変更するということである(物体の表面や流入)。これはどういうことかというと、
$$
\frac{\partial p}{\partial x} = \frac{p_{i,j+1} - p_{i,j}}{\delta} = 0
$$
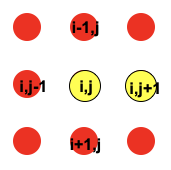
なので$p_{i,j+1} = p_{i,j}$となる。図形的に考えると、以下の黄丸の値が等しいということになる。
これをPoisson方程式に当てはめると
$$
3p_{i,j} - p_{i+1,j} - p_{i-1,j} - 0 - p_{i,j-1} = - s_{i,j}
$$
それでは、この形を含むPoisson方程式の行列を作成してみる。先ほどの例で境界条件が全てflag_p = 2であるときを考えてみる。
グリッド数 : 4x4
速度の数 : 4x4 青丸
圧力の数 : 5x5 赤丸、緑丸
緑丸は境界条件flag_p = 2
対角成分が2,3,4である行列ができる。
\left[
\begin{array}{c}
2 & -1 & 0 & -1 & 0 & & \cdots & & 0 \\
-1 & 3 & -1 & 0 & -1 & 0 & & & \\
0 & -1 & 2 & 0 & 0 & -1 & 0 & & \vdots \\
-1 & 0 & 0 & 3 & -1 & 0 & -1 & 0 & \\
0 & -1 & 0 & -1 & 4 & -1 & 0 & -1 & 0 \\
& 0 & -1 & 0 & -1 & 3 & 0 & 0 & -1 \\
\vdots & & 0 & -1 & 0 & 0 & 2 & -1 & 0 \\
& & & 0 & -1 & 0 & -1 & 3 & -1 \\
0 & & \cdots & & 0 & -1 & 0 & -1 & 2 \\
\end{array}
\right]
\left[
\begin{array}{c}
p_{11} \\
p_{12} \\
p_{13} \\
p_{21} \\
p_{22} \\
p_{23} \\
p_{31} \\
p_{32} \\
p_{33} \\
\end{array}
\right] = -
\left[
\begin{array}{c}
s_{11} \\
s_{12} \\
s_{13} \\
s_{21} \\
s_{22} \\
s_{23} \\
s_{31} \\
s_{32} \\
s_{33} \\
\end{array}
\right]
物体の内部
物体の内部(flag = 3)は周りの値に関わらず、$p=0$にならなければいけないため、Poisson方程式は
$$
p_{i,j} - 0 - 0 - 0 - 0 = -0
$$
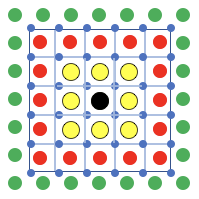
最後に、物体が存在する状態で行列を作成してみる。
グリッド数 : 6x6
速度の数 : 6x6 青丸
圧力の数 : 7x7 緑丸、赤丸、黄丸、黒丸
緑丸は境界条件flag_p = 1
赤色は境界条件flag_p = 0
黄色は境界条件flag_p = 2
黒色は境界条件flag_p = 3
flag_p
[[1. 1. 1. 1. 1. 1. 1.]
[1. 0. 0. 0. 0. 0. 1.]
[1. 0. 2. 2. 2. 0. 1.]
[1. 0. 2. 3. 2. 0. 1.]
[1. 0. 2. 2. 2. 0. 1.]
[1. 0. 0. 0. 0. 0. 1.]
[1. 1. 1. 1. 1. 1. 1.]]
行列A
[4, -1, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[-1, 3, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, -1, 3, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, -1, 3, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, -1, 4, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[-1, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, -1, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 3, 0, 0, 0, 0, -1]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 4, -1, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 3, -1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 3, -1, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 3, -1]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, -1, 4]
対角成分が1,2,3,4のいづれかとなり、対角成分以外も不規則になったが、対称性は保たれていることがわかる。
以下が行列Aを作成するコードです。もっと冗長にかける方法があれば知りたいです。Aは疎行列なので、scipyのspars.csc_matrixで疎行列に変換しています。cholesky分解をsksparse.cholmodのcholeskyで行なっているのでcscフォーマットが良いです。
def initA(flag_p):
N = num_Ax * num_Ay
A = np.eye(N) * 4
for i in range(N):
if flag_p[i // num_Ax + 1, i % num_Ax + 1] >= 2:
A[i, i] = 1
continue
Apij = [
[i, i-num_Ax, i // num_Ax, i % num_Ax + 1],
[i, i-1, i // num_Ax + 1, i % num_Ax],
[i, i+1, i // num_Ax + 1, i% num_Ax + 2],
[i, i+num_Ax, i // num_Ax + 2, i % num_Ax + 1]
]
for Ai, Aj, pi, pj in Apij:
if flag_p[pi, pj] == 2:
A[Ai, Ai] -= 1
if Aj < 0 or Aj >= N:
continue
if flag_p[pi, pj] >= 1 or pi == 0 or pi == num_py-1 \
or pj == 0 or pj == num_px-1:
A[Ai, Aj] = 0
else:
A[Ai, Aj] = -1
A = scipy.sparse.csr_matrix(A)
return A
Poisson方程式の右辺を計算する
$$
s = \nabla \vec{v}' / \Delta t
$$
$$
\nabla \vec{v}' = \frac{1}{2 \delta} ( u_{i-1,j} - u_{i-1,j-1} + u_{i,j} - u_{i,j-1} + v_{i,j-1} - v_{i-1,j-1} + v_{i,j} - v_{i-1,j} )
$$
def DiverV(s, u, v, flag_v):
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_v[i, j] >= 3 or flag_v[i-1, j] >= 3 or flag_v[i-1, j-1] >= 3 or flag_v[i, j-1] >= 3:
continue
if flag_v[i, j] == 2:
if i == num_py-2: u[i, j], v[i, j] = u[i-1, j], v[i-1, j]
else: u[i, j], v[i, j] = u[i, j-1], v[i, j-1]
if flag_v[i-1, j] == 2:
if i-1 == 0: u[i-1, j], v[i-1, j] = u[i, j], v[i, j]
else: u[i-1, j], v[i-1, j] = u[i-1, j-1], v[i-1, j-1]
if flag_v[i, j-1] == 2:
if i == num_py-2: u[i, j-1], v[i, j-1] = u[i-1, j-1], v[i-1, j-1]
else: u[i, j-1], v[i, j-1] = u[i, j], v[i, j]
if flag_v[i-1, j-1] == 2:
if i-1 == 0: u[i-1, j-1], v[i-1, j-1] = u[i, j-1], v[i, j-1]
else: u[i-1, j-1], v[i-1, j-1] = u[i-1, j], v[i-1, j]
s[i, j] = (
u[i-1, j] - u[i-1, j-1] + u[i, j] - u[i, j-1] + \
v[i, j-1] - v[i-1, j-1] + v[i, j] - v[i-1, j]
) * delta / (2*delta_t)
return
cholesky分解で圧力を求める
行列Aをsksparse.cholmod.choleskyで前処理してから以下の関数に渡す。Poisson方程式右辺の$s$は流入、流出境界を含んでおり、行列Aは含んでいないので注意する。Cholesky分解の結果はベクトルなので行列に戻す作業も必要。
factor = cholesky(A)
def Cholesky(p, s, flag_p, factor):
s = s[1:-1, 1:-1] * -1
b = s.reshape((-1,))
x = factor(b)
x = x.reshape((num_Ay, num_Ax))
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_p[i, j] >= 1: continue
p[i, j] = x[i-1, j-1]
if flag_p[i+1, j] == 2: p[i+1, j] = x[i-1, j-1]
if flag_p[i-1, j] == 2: p[i-1, j] = x[i-1, j-1]
if flag_p[i, j+1] == 2: p[i, j+1] = x[i-1, j-1]
if flag_p[i, j-1] == 2: p[i, j-1] = x[i-1, j-1]
return
3. 圧力からn+1番目の速度を求める
$$
\vec{v}^{n+1} = \vec{v}' - \nabla p^{n+1}
$$
離散化すると
$$
u^{n+1} = u' - \frac{\Delta t}{2 \delta} \left(p_{i,j+1} - p_{i,j} + p_{i+1,j+1} - p_{i+1,j} \right)
$$
$$
v^{n+1} = v' - \frac{\Delta t}{2 \delta} \left(p_{i+1,j} - p_{i,j} + p_{i+1,j+1} - p_{i,j+1} \right)
$$
def UpdateV(u, v, p, flag_v):
for i in range(1, num_vy-1):
for j in range(1, num_vx-1):
if flag_v[i, j] >= 1: continue
u[i, j] -= (p[i, j+1] - p[i, j] + p[i+1, j+1] - p[i+1, j]) * delta_t / (2*delta)
v[i, j] -= (p[i+1, j] - p[i, j] + p[i+1, j+1] - p[i, j+1]) * delta_t / (2*delta)
return
計算条件
- 速度のグリッド数 : 90x60 (境界のグリッドを合わせると92x62)
- Δx = Δy = 0.5
- Δt = 0.05
- レイノルズ数 : 100
- 物体の大きさ : 5 x 5の正方形
- 物体の配置 : 物体の中心の座標が(15, 15)
上記の条件で時間ステップを1000回ほど進める(約3分)とカルマン渦ができ始める。
グリッド数を増やして遊んでみるのも面白い。
補足1
SOR法、CG法、Cholesky分解のグリッド数の違いによる速度比較を行いました。
時間step数が100までの計算時間です
| grid size | Cholesky [sec] | CG [sec] | SOR [sec] |
|---|---|---|---|
| 90x60 | 12.02 | 13.85 | 358.44 |
| 100x100 | 22.47 | 28.53 | - |
| 100x150 | 32.28 | 42.26 | - |
| 200x200 | 88.05 | 116.53 | - |
Cholesky分解の方がCG法より若干早いですね。SOR法は結果が明らかに遅いので途中から計算するのをやめました、、、。Cholesky分解とCG法はライブラリーを使ったのでもしかしたら並列計算とかしているのかな、、、
以下、それぞれの計算条件について
Cholesky分解
-
sksparse.cholmod.choleskyを使用 - コードはこの記事で紹介済み
CG法
-
scipy.sparse.linalg.isolve.cgを使用 - 収束判定値 : 1e-06
def CG(p, s, flag_p, A):
s = s[1:-1, 1:-1] * -1
b = s.reshape((-1,))
x, info = cg(A, b, tol=1e-06)
if info != 0:
print(info)
x = x.reshape((num_Ay, num_Ax))
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_p[i, j] >= 1: continue
p[i, j] = x[i-1, j-1]
if flag_p[i+1, j] == 2: p[i+1, j] = x[i-1, j-1]
if flag_p[i-1, j] == 2: p[i-1, j] = x[i-1, j-1]
if flag_p[i, j+1] == 2: p[i, j+1] = x[i-1, j-1]
if flag_p[i, j-1] == 2: p[i, j-1] = x[i-1, j-1]
return
SOR法
- 収束判定値 : 1e-06
- 最大反復回数 : 100 (この値では一度も収束しませんでした。。。)
- ω = 1.8
def SOR(p, s, flag_p, omega):
error = 0
target_error = 1e-6
for m in range(100):
for i in range(1, num_py-1):
for j in range(1, num_px-1):
if flag_p[i+1, j] >= 3 or flag_p[i-1, j] >= 3 or flag_p[i, j+1] >= 3 or flag_p[i, j-1] >= 3 or flag_p[i, j] >= 2: continue
if flag_p[i+1, j] == 2: p[i+1, j] = p[i, j]
if flag_p[i-1, j] == 2: p[i-1, j] = p[i, j]
if flag_p[i, j+1] == 2: p[i, j+1] = p[i, j]
if flag_p[i, j-1] == 2: p[i, j-1] = p[i, j]
tmp = (p[i+1, j] + p[i-1, j] + p[i, j+1] + p[i, j-1] - s[i, j]) / 4
error = max(error, abs(p[i, j] - tmp))
p[i, j] = (1.0 - omega) * p[i, j] + omega*tmp
if (error < target_error):
print(f"converge! m={m} error={error}")
break
return
最後に
この記事は独学の試行錯誤によるものです。何か間違い等ありましたらお知らせください。よろしくお願いいたします。