直線に垂直な円の接線の方程式を求める

直線に垂直な円の接線の方程式を求める

直線 $ax+by+c=0$ に垂直な、中心が $(x_0,y_0)$ 半径が $r$ の円 $(x-x_0)^2+(y-y_0)^2=r^2$ の2つの接線の方程式を求める。

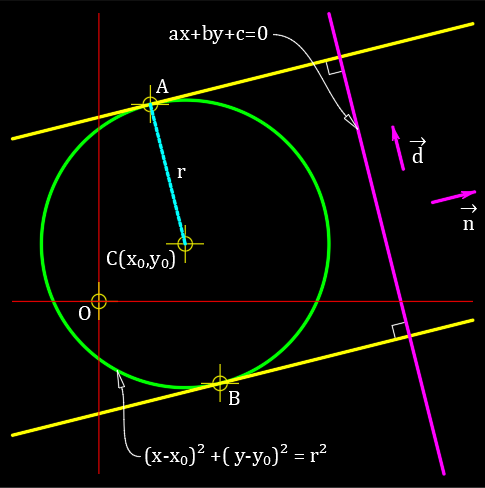
求める接線は、直線 $ax+by+c=0$ に垂直なのでその方向ベクトルは、直線の法線ベクトルになる。
直線 $ax+by+c=0$ の法線ベクトルは、
$$\vec{n}=(a,b)$$
よって接線の傾き $m$ は、
$$m=\frac{b}{a}$$
となる。

接点 $A$ は、円の中心 $(x_0,y_0)$ から直線の方向ベクトル $\vec{d}$ 方向に 距離 $r$ の点と考えられる。
点 $C(x_0,y_0)$ に、直線の方向ベクトル $\vec{d}$ の単位ベクトルを $r$ 倍したベクトルをたすことで求めることができる。
接点 $B$ は、点 $C(x_0,y_0)$ に、直線の方向ベクトル $\vec{d}$ の単位ベクトルに $-r$ 倍したベクトルをたすことで求めることができる。

直線 $ax+by+c=0$ の方向ベクトルは、
$$\vec{d}=(-b,a)$$
$\vec{d}$ の単位ベクトルを $\vec{k}$ とすると、
$$\vec{k}=(-b,a)\cdot\frac{1}{\sqrt{a^2+b^2}}=\left(-\frac{b}{\sqrt{a^2+b^2}},\frac{a}{\sqrt{a^2+b^2}}\right)$$
となり接点 $A,B$ の座標は、
$$A=(x_0,y_0)+\left(-\frac{b}{\sqrt{a^2+b^2}}\cdot r,\frac{a}{\sqrt{a^2+b^2}}\cdot r\right)=\left(-\frac{br}{\sqrt{a^2+b^2}}+x_0,\frac{ar}{\sqrt{a^2+b^2}}+y_0\right)$$
$$B=(x_0,y_0)+\left(-\frac{b}{\sqrt{a^2+b^2}}\cdot -r,\frac{a}{\sqrt{a^2+b^2}}\cdot -r\right)=\left(\frac{br}{\sqrt{a^2+b^2}}+x_0,-\frac{ar}{\sqrt{a^2+b^2}}+y_0\right)$$
となる。
接点 $A$ 側の接線は、点 $A$ を通る傾きが $\dfrac{b}{a}$ の直線と考えられるので、直線の方程式の1点と傾きが与えられた直線の公式より、
$$y-\left(\frac{ar}{\sqrt{a^2+b^2}}+y_0\right)=\frac{b}{a}\Biggl\{x-\left(-\frac{br}{\sqrt{a^2+b^2}}+x_0\right)\Biggr\}$$
この式の両辺に $a$ を掛けて、
$$a\left(y-\frac{ar}{\sqrt{a^2+b^2}}-y_0\right)=b\left(x+\frac{br}{\sqrt{a^2+b^2}}-x_0\right)$$
両辺を展開して、
$$ay-\frac{a^2r}{\sqrt{a^2+b^2}}-ay_0=bx+\frac{b^2r}{\sqrt{a^2+b^2}}-bx_0$$
右辺を左辺に移項すると、
$$-bx+ay+bx_0-ay_0-\left(\frac{a^2r}{\sqrt{a^2+b^2}}+\frac{b^2r}{\sqrt{a^2+b^2}}\right)=0$$
ここで、
$$\left(\frac{a^2r}{\sqrt{a^2+b^2}}+\frac{b^2r}{\sqrt{a^2+b^2}}\right)=\frac{a^2r+b^2r}{\sqrt{a^2+b^2}}=\frac{(a^2+b^2)r}{\sqrt{a^2+b^2}}=\frac{(a^2+b^2)\sqrt{a^2+b^2}}{a^2+b^2}r=r\sqrt{a^2+b^2}$$
よって、
$$-bx+ay+bx_0-ay_0-r\sqrt{a^2+b^2}=0$$
両辺に $-1$ を掛けて、
$$bx-ay-(bx_0-ay_0-r\sqrt{a^2+b^2})=0$$
となる。これが接点 $A$ 側の接線の方程式です。
同様に接点 $B$ 側の接線の方程式を計算すると、
$$bx-ay-(bx_0-ay_0+r\sqrt{a^2+b^2})=0$$
となる。

直線方程式 $ax+by+c=0$ が正規化されている場合、（直線の方程式を正規化する 参照）
接線の方程式は、
$$bx-ay-(bx_0-ay_0-r)=0$$
$$bx-ay-(bx_0-ay_0+r)=0$$
となる。

【例】中心(3,2) 半径 5 の円に対して、直線 3x+4y-50=0 に垂直な接線の方程式を求める。

上記公式 $bx-ay-(bx_0-ay_0-r\sqrt{a^2+b^2})=0$ より、
$4x-3y-(4\cdot3-3\cdot2-5\sqrt{3^2+4^2})=0$ よって接線の方程式は、
$$4x-3y+19=0$$
公式 $bx-ay-(bx_0-ay_0+r\sqrt{a^2+b^2})=0$ より、
$4x-3y-(4\cdot3-3\cdot2+5\sqrt{3^2+4^2})=0$ よって、
$$4x-3y-31=0$$
となる。

サンプルプログラム

円図形を選択して、その次に直線(LINE,XLINE,RAY)を選択。選択した直線に垂直な円の接線を作成する。

;; 直線に垂直な円の接線を作成
(defun c:CreateTangentOfPerpendicularLine (/ circle line tangents)
    ;; 円を選択
    (while (null circle)
        (setvar 'ERRNO 0)
        (setq circle (car (entsel "円を選択: ")))
        (cond
            ;; 空振り
            ((= 7 (getvar 'ERRNO))
             (princ "\n**空振り!!再選択**\n")
             (setq circle nil)
            )
            ;; 空Enter
            ((= 52 (getvar 'ERRNO))
             (princ "\n**空Enter!!再選択**\n")
             (setq circle nil)
            )
            ;; 図形が選択された
            (circle
             (if (/= "CIRCLE" (entity:GetType circle))
                 (progn
                     (princ "\n**円ではありません!!再選択**\n")
                     (setq circle nil)
                 )
                 (princ "\n**円が選択されました。**\n")
             )
            )
        )
    )
    ;; 直線を選択
    (while (null line)
        (setvar 'ERRNO 0)
        (setq line (car (entsel "直線を選択: ")))
        (cond
            ;; 空振り
            ((= 7 (getvar 'ERRNO))
             (princ "\n**空振り!!再選択**\n")
             (setq line nil)
            )
            ;; 空Enter
            ((= 52 (getvar 'ERRNO))
             (princ "\n**空Enter!!再選択**\n")
             (setq line nil)
            )
            ;; 図形が選択された
            (line
             (setq e (entity:GetType line))
             (if (and (/= "LINE" e) (/= "RAY" e) (/= "XLINE" e))
                 (progn
                     (princ "\n**直線ではありません!!再選択**\n")
                     (setq line nil)
                 )
                 (princ "\n**直線が選択されました。**\n")
             )
            )
         )
    )
    ;; 接線の方程式を取得
    (setq tangents (circle:GetEquationOfTangentPerpendicularToLine circle line))
    ;; 構築線を作成
    (mapcar
        (function
            (lambda (f)
                (entmake:XlineFromEquation (car f) (cadr f) (caddr f))
            )
        )
        tangents
    )
)

;; == sub functions ==
;; 図形のDXF定義データの値を取得
(defun entity:GetDxf (g e)
    (cond
        ((= (type e) 'ENAME) (cdr (assoc g (entget e))))
        ((listp e) (cdr (assoc g e))) 
    )
)
;; 図形のタイプを取得
(defun entity:GetType (e) (entity:GetDxf 0 e))
;; 2点から直線の方程式を求める ax + by + c = 0
;; 正規化された (a b c) のリストを返す
(defun geometric:GetLineEquation (p1 p2 / x1 y1 x2 y2 l)
    (setq x1 (car p1) y1 (cadr p1)
          x2 (car p2) y2 (cadr p2)
          len (distance p1 p2) ;; p1-p2の距離
    )
    (if (> len 1.0e-08)
        (mapcar
            (function
                (lambda (x) (/ x len))
	    )
	    (list (- y2 y1) (- x1 x2) (- (* x2 y1) (* x1 y2)))
        )
    )
)
;; 図形が線分かどうか調べる
(defun entity:IsLine (e) (= "LINE" (entity:GetType e)))
;; 図形が構築線かどうか調べる
(defun entity:IsXline (e) (= "XLINE" (entity:GetType e)))
;; 図形が放射線かどうか調べる
(defun entity:IsRay (e) (= "RAY" (entity:GetType e)))
;; 円の中心を取得
(defun circle:GetCenter (e) (entity:GetDxf 10 e))
;; 円の半径を取得
(defun circle:GetRadius (e) (entity:GetDxf 40 e))
;; 線分の始点を取得
(defun line:GetStartPoint (e) (entity:GetDxf 10 e))
;; 線分の終点を取得
(defun line:GetEndPoint (e) (entity:GetDxf 11 e))
;; 線分の始点-終点のリストを取得
(defun line:GetStartAndEndPoints (e)
    (list (line:GetStartPoint e) (line:GetEndPoint e))
)
;; 構築線の基点を取得
(defun xline:GetFirstPoint (e) (entity:GetDxf 10 e))
;; 構築線の単位方向ベクトルを取得
(defun xline:GetUnitVector (e) (entity:GetDxf 11 e))
;; 構築線の基点から単位方向ベクトルの点を計算
(defun xline:GetSecondPoint (e)
    (mapcar '+ (xline:GetFirstPoint e) (xline:GetUnitVector e))
)
;; 構築線上の2点をを取得
(defun xline:GetFirstAndSecondPoints (e)
    (list (xline:GetFirstPoint e) (xline:GetSecondPoint e))
)
;; 放射線の始点を取得
(defun ray:GetFirstPoint (e) (entity:GetDxf 10 e))
;; 放射線の単位方向ベクトルを取得
(defun ray:GetUnitVector (e) (entity:GetDxf 11 e))
;; 放射線の基点から単位方向ベクトルの点を計算
(defun ray:GetSecondPoint (e)
    (mapcar '+ (ray:GetFirstPoint e) (ray:GetUnitVector e))
)
;; 放射線上の2点をを取得
(defun ray:GetFirstAndSecondPoints (e)
    (list (ray:GetFirstPoint e) (ray:GetSecondPoint e))
)
;; 線状図形上の2点を取得
(defun entity:Get2PointsOfLinear (e)
    (cond
        ((entity:IsLine e) (line:GetStartAndEndPoints e))
        ((entity:IsXline e) (xline:GetFirstAndSecondPoints e))
        ((entity:IsRay e) (ray:GetFirstAndSecondPoints e))
    )
)
;; 線状図形上の2点から直線の方程式を求める
(defun geometric:GetLineEquationFromLinear (linear / points)
    (setq points (entity:Get2PointsOfLinear linear))
    (geometric:GetLineEquation (car points) (cadr points))
)
;; 直線に垂直な接線の方程式
(defun circle:GetEquationOfTangentPerpendicularToLine (circle line / a b c d r o)
    (setq f (geometric:GetLineEquationFromLinear line))
    (setq r (circle:GetRadius circle)
          o (circle:GetCenterPoint circle)
          a (car f)
          b (cadr f)
          ;;c (caddr f)
    )
    (list
        (list b (- a) (+ (- (* b (car o))) (* a (cadr o)) r))
        (list b (- a) (- (+ (- (* b (car o))) (* a (cadr o))) r))
    )
)
;; 構築線を定義
(defun entmake:XlineBase (p u)
    (list '(000 . "XLINE")
	  '(100 . "AcDbEntity")
	  '(100 . "AcDbXline")
	  (cons 010 p)
	  (cons 011 u)
    )
)
;; 基点と単位方向ベクトルから構築線を作成
(defun entmake:Xline (p u) (entmake (entmake:XlineBase p u)) (entlast))
;; 直線の方程式から構築線を作成
(defun entmake:XlineFromEquation (a b c)
    (entmake:Xline (list (- (/ c a)) 0. 0.) (list (- b) a 0.))
)