基本形
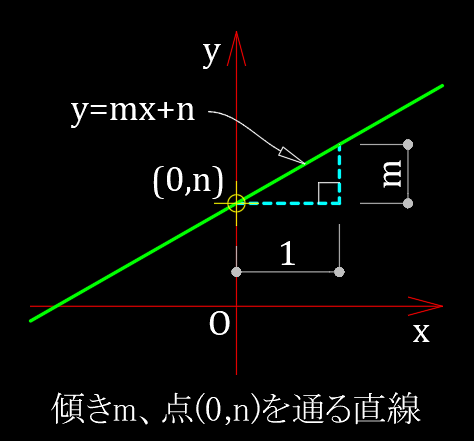
傾きが $m$ で、点$(0,n)$ を通る直線の方程式は、
$$\bf y=mx+n$$
で表される。( $y$ 切片が $n$ )
$m=0$ のとき、$y=n$ となり、これは$x$軸に平行な直線を表す。
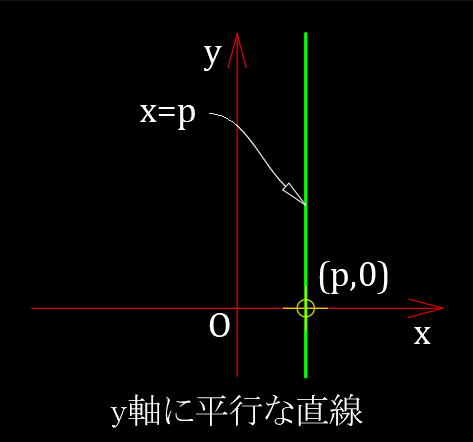
$y$ 軸に平行な直線($x=p$ の形の直線)はこの形では表現できない。

一般形
直線の方程式 $y=mx+n$ の右辺を左辺に移項してして整理すれば、
$mx-y+n=0$ となり、これは $x,y$ に関する一般的な形の1次方程式
$$\bf ax+by+c=0 \ (a\neq 0 \ または \ b\neq0)$$
の形をしている。これが直線の方程式の一般形。
この形ならば、$y$軸に平行な直線も表現できる。
この形の欠点は、1つの直線の表現が一意に定まらない、つまり、
$3x-2y-4=0$ と $x-\frac{2}{3}y-\frac{4}{3}=0$ は同じ直線を表す。
この方程式は$x$と$y$ に関する1次方程式であるので、$x$と$y$ の係数 $a$と$b$ が同時に $0$ になることはない。
すなわち、$a=0,b=0$ となることはない。
$a\neq0,b\neq0$ のとき、$ax+by+c=0$ は、
$$y=-\frac{a}{b}x-\frac{c}{b}$$
と書き換えられるので、これは傾きが $-\dfrac{a}{b}$、$y$ 切片が$-\dfrac{c}{b}$の直線を表す。
$a\neq0,b=0$ のとき、$ax+by+c=0$ は、
$$x=-\frac{c}{a}$$
となる。これは、$y$ 軸に平行な直線を表す。
$a=0,b\neq0$ のとき、$ax+by+c=0$ は、
$$y=-\frac{c}{b}$$
となる。これは、$x$ 軸に平行な直線を表す。
また、
直線 $ax+by+c=0$ において、係数の組 $(a,b)$ はこの直線の法線ベクトルの1つを表す。
(直線のベクトル方程式 参照)
【例】方程式 $3x-2y-4=0$ の表す図形を書く
この式を変形すると、
$$ y=\frac{3}{2}x-2$$
となる。これは傾きが $-\dfrac{3}{2}$、$y$ 切片が$-2$の直線を表す。

1点と傾きが与えられた直線
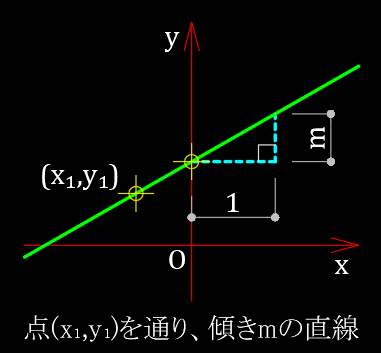
点$(x_1,y_1)$ を通り、傾きが $m$ の直線は、$y$ 切片を $n$ とすると、直線の方程式の標準形、
$$y=mx+n$$
で表すことができる。この直線が、点$(x_1,y_1)$ を通るので、
$y_1=mx_1+n$ すなわち、$n=y_1-mx_1$
これを元の標準形の式に代入すると、
$y=mx+y_1-mx_1$ となり、$y_1$ を左辺に移項して、右辺を$m$でくくると、
$$\bf y-y_1=m(x-x_1)$$
となる。これが点$(x_1,y_1)$ を通り、傾きが $m$ の直線の方程式です。
2点を通る直線
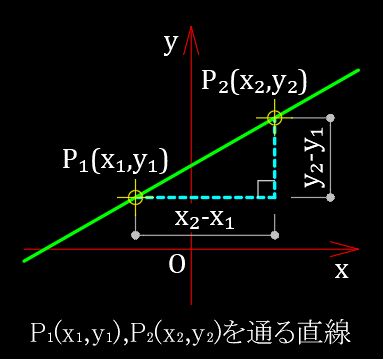
2点 $P_1(x_1,y_1)$、$P_2(x_2,y_2)$ を通る直線は、
$x_1\neq x_2$ のとき、
この直線の傾きは、$\dfrac{y_2-y_1}{x_2-x_1}$ で点 $(x_1,y_1)$ を通るので、
1点と傾きが与えられた直線の式 $y-y_1=m(x-x_1)$ により、
$$\bf y-y_1=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$$
となる。これが2点 $(x_1,y_1)$、$(x_2,y_2)$ を通る直線の方程式です。
この式は、$x_1=x_2$ の場合、右辺の分母が $0$ になるので成立しない。
したがって、$y$ 軸に平行な直線を表現できない。
この式を変形して、
(1) 右辺と左辺を入れ替える
$\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)=y-y_1$
(2) 両辺に $(x_2-x_1)$ を掛ける
$(x-x_1)(y_2-y_1)=(x_2-x_1)(y-y_1)$
(3) 展開する
$xy_2-xy_1-x_1y_2+x_1y_1=x_2y-x_2y_1-x_1y+x_1y_1$
(4) 両辺に $x_1y_1$ があるので消す。左辺を$x$、右辺を$y$でくくる
$(y_2-y_1)x-x_1y_2=(x_2-x_1)y-x_2y_1$
この式の右辺を左辺に移項すると、
$$\bf (y_2-y_1)x-(x_2-x_1)y-(x_1y_2-x_2y_1)=0$$
となる。これも2点 $(x_1,y_1)$、$(x_2,y_2)$ を通る直線の方程式です。
さらに符号を$+$に変えて、
$$\bf (y_2-y_1)x+(x_1-x_2)y+(x_2y_1-x_1y_2)=0$$
この式は、直線の方程式の一般形 $ax+by+c=0$ の形をしている。
2点から直線の方程式を求めるプログラム
直線の方程式をプログラムで扱う場合は、正規化すると便利。
;; 2点から直線の方程式を求める ax + by + c = 0
;; 点p1,p2 から 直線の方程式の係数 a , b , c のリストを返す
;; 2点間の距離(len)で割って正規化する
;; Args - p1, p2 : 点のリスト
(defun line:GetEquation (p1 p2 / x1 y1 x2 y2 l)
(setq x1 (car p1) y1 (cadr p1)
x2 (car p2) y2 (cadr p2)
len (distance p1 p2) ;; p1-p2の距離
)
(if (> len 1.0e-08)
(mapcar
(function
(lambda (x) (/ x len))
)
(list (- y2 y1) (- x1 x2) (- (* x2 y1) (* x1 y2)))
)
)
)
;; < Example >
(line:GetEquation '(2 3) '(10 -1))
;; -> (-0.447214 -0.894427 3.57771)
(line:GetEquation '(2 3) '(10 5))
;; -> (0.242536 -0.970143 2.42536)
(line:GetEquation '(6 -2) '(4 2))
;; -> (0.894427 0.447214 -4.47214)
(line:GetEquation '(2 0) '(2 -9))
;; -> (-1.0 0.0 2.0)