1点を通り、与えられたベクトルに平行な直線
点 $A(\vec{a})$ を通り、$\vec{0}$ でないベクトル $\vec{d}$ に平行な直線

点 $A(\vec{a})$ 以外のこの直線上の任意の点を $P(\vec{p})$ とすれば、ベクトル $\overrightarrow{AP}$ は $\vec{d}$ に平行なので、
動点 $P$ がこの直線上の点であるということは、
$$\overrightarrow{AP}=t \vec{d}$$
となるような、実数 $t$ が存在することと同じこと。
この式を位置ベクトルを使って書き直せば、
$\overrightarrow{AP}=\vec{p}-\vec{a}$ なので、$\vec{p}-\vec{a}=t \vec{d}$ すなわち、
$$\vec{p}=\vec{a}+t\vec{d}$$
これがこの直線のベクトル方程式。
$t$ を媒介変数(ばいかいへんすう)または、パラメータ、$\vec{d}$ をこの直線の方向ベクトルという。
点 $A$ の座標を $(x_1,y_1)$ 、方向ベクトル $\vec{d}=(l,m)$ のとき、
動点 $P$ の座標を $(x,y)$ とすると、
$$(x,y)=(x_1,y_1)+t(l,m)$$
すなわち、
\left\{
\begin{array}{ll}
x=x_1+lt \\
y=y_1+mt
\end{array}
\right.
と書き表せる。これを直線の媒介変数表示をいう。
$\vec{d}$ は $\vec{0}$ ではないので、$l,m$ の少なくとも一方は $0$ ではない、
すなわち、$l=0,m=0$ となることはない。
$l=0,m\neq0$ のとき、この連立方程式は、
\left\{
\begin{array}{ll}
x=x_1 \\
y=y_1+mt
\end{array}
\right.
となる。これは、$y$ 軸に平行な直線を表す。
$l\neq0,m=0$ のとき、この連立方程式は、
\left\{
\begin{array}{ll}
x=x_1+lt \\
y=y_1
\end{array}
\right.
となる。これは、$x$ 軸に平行な直線を表す。
$l\neq0,m\neq0$ のとき、この連立方程式は、
\left\{
\begin{array}{ll}
x=x_1+lt \\
y=y_1+mt
\end{array}
\right.
\Longrightarrow
\left\{
\begin{array}{ll}
lt=x-x_1 \\
mt=y-y_1
\end{array}
\right.
\Longrightarrow
\left\{
\begin{array}{ll}
t=\frac{x-x_1}{l} \\
t=\frac{y-y_1}{m}
\end{array}
\right.
と変形して、
$$\frac{x-x_1}{l}=\frac{y-y_1}{m}$$
両辺に $m$ を掛けて、
$$y-y_1=\frac{m}{l}(x-x_1)$$
となる。これは直線の方程式の標準形の形で、
点 $(x_1,y_1)$ を通る、傾きが $\dfrac{m}{l}$ の直線を表す。
2点を通る直線
2点 $A(\vec{a}),B(\vec{b})$ を通る直線
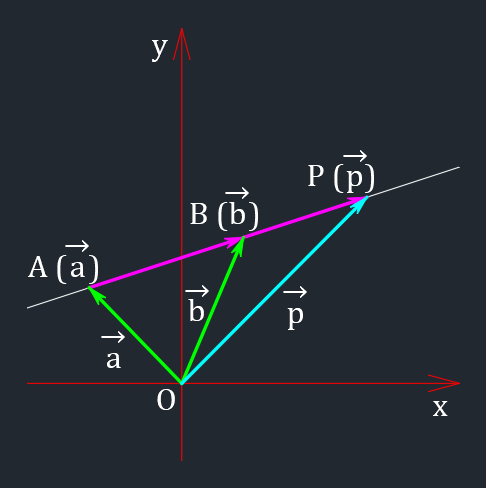
この直線は、点 $A(\vec{a})$ を通り、$\overrightarrow{AP}=\vec{b}-\vec{a}$ を方向ベクトルとする直線と考えられる。
ゆえにこの直線のベクトル方程式は、
方向ベクトル $\vec{d}=\vec{b}-\vec{a}$、直線のベクトル方程式 $\vec{p}=\vec{a}+t\vec{d}$ より、
$$\vec{p}=\vec{a}+t(\vec{b}-\vec{a})=\vec{a}+t\vec{b}-t\vec{a}$$
となり、
$$\vec{p}=(1-t)\vec{a}+t\vec{b}$$
となる。 $1-t=s$ とおけば、
$$\vec{p}=s\vec{a}+t\vec{b}\ ,\ s+t=1\ (係数の和が1)$$
という表現にできる。
1点を通り、与えられたベクトルに垂直な直線
点 $A(\vec{a})$ を通り、$\vec{0}$ でないベクトル $\vec{n}$ に垂直な直線

点 $A(\vec{a})$ 以外のこの直線上の任意の点を $P(\vec{p})$ とすれば、ベクトル $\overrightarrow{AP}$ は $\vec{n}$ に垂直なので、
動点 $P$ がこの直線上の点であるということは、
$$\vec{n} \cdot \overrightarrow{AP}=0$$
であることと同じこと。(内積が $0$)
この式を位置ベクトルを使って書き直せば、
$\overrightarrow{AP}=\vec{p}-\vec{a}$ なので、
$$\vec{n} \cdot (\vec{p}-\vec{a})=0$$
これがこの直線のベクトル方程式。
$\vec{n}$ をこの直線の法線ベクトルという。
点 $A$ の座標を $(x_1,y_1)$ 、法線ベクトル $\vec{n}=(a,b)$ のとき、
動点 $P$ の座標を $(x,y)$ とすると、
$\ \vec{p}-\vec{a}=(x-x_1, y-y_1)$
$\ \vec{n} \cdot (\vec{p}-\vec{a})=a(x-x_1)+b(y-y_1)$
なので、
$$a(x-x_1)+b(y-y_1)=0$$
これが、この直線を座標によって表した方程式。
さらにこの式を展開して、
$ax-ax_1+by-by_1=0$
並び替えて、
$ax+by+(-ax_1-by_1)=0$
$(-ax_1-by_1)=c$ とおくと、
$$ax+by+c=0$$
となり、これは直線の方程式の一般形である。
このことから、
直線 $ax+by+c=0$ において、係数の組 $(a,b)$ はこの直線の法線ベクトルの1つを表す。