3点が同一直線上の点か調べる

調べ方

3点の回転方向を調べる
にて、
$dx2 \times dy1 = dx1 \times dy2$ の場合は、

3点は同一直線上の点であることがわかる。

例

$A=(2,3), B=(7,6), C=(12,9)$ のとき

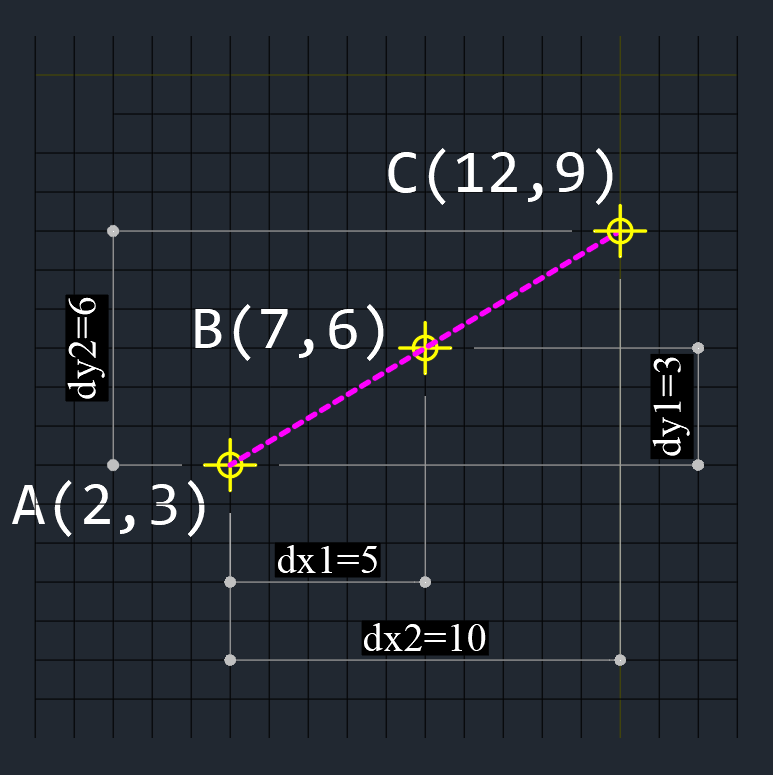
$dx2 \times dy1 = 10 \times 3 = 30$
$dx1 \times dy2 = 5 \times 6 = 30$
$dx2 \times dy1 = dx1 \times dy2$ なので 3点は同一線直線上の点。

3点が同一直線上の点の場合の配置パターン

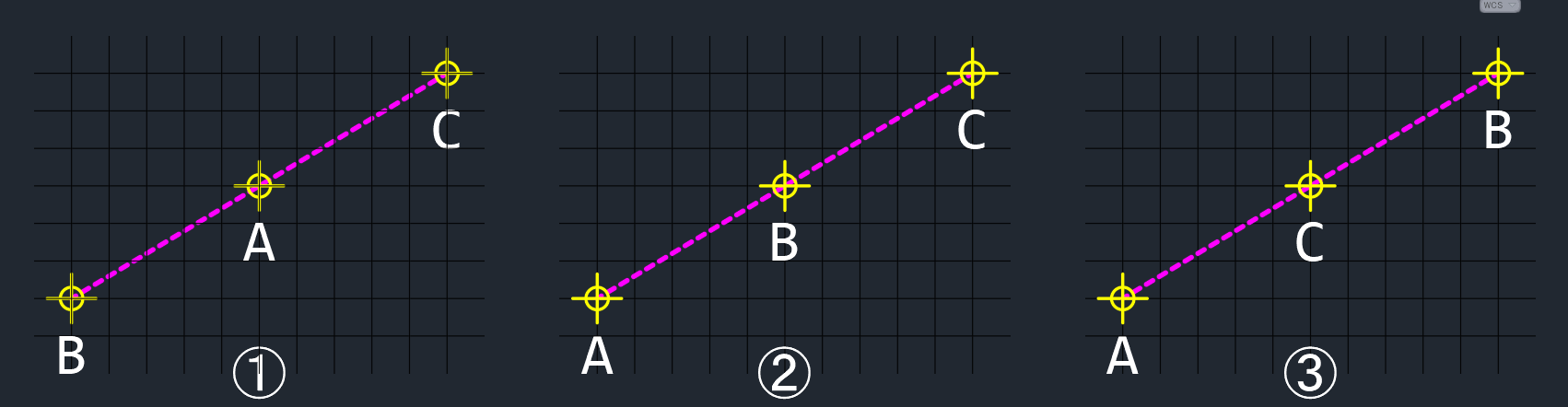
① 点Aが点B,Cの間に配置されている
② 点Bが点A,Cの間に配置されている
③ 点Cが点A,Bの間に配置されている
のいずれかになる。

3点が同一直線上の点の場合の配置パターンの判定

① 点Aが点B,Cの間に配置されている

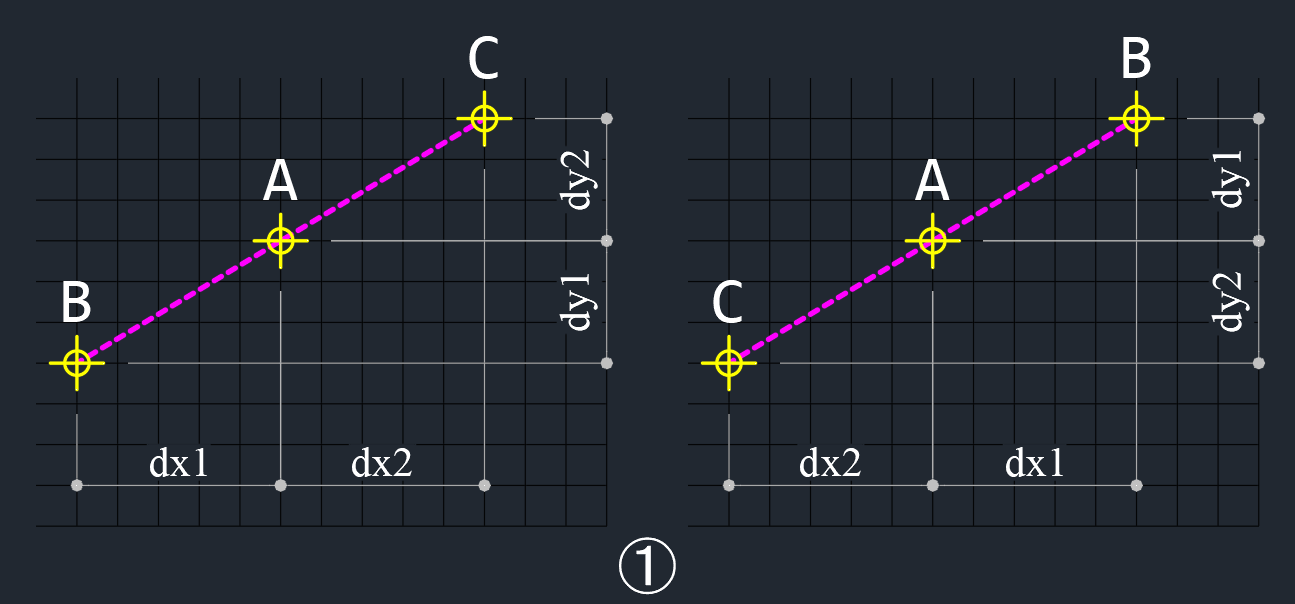
このとき、点Aを基点としているので、
dx1,dx2 のいずれか1つは負の数、
dy1,dy2 のいずれか1つは負の数になるので、
$dx2 \times dy1 = dx1 \times dy2$ かつ、
$dx1 \times dx2 < 0$ または、$dy1 \times dy2 < 0$
の場合、点Aが点B,Cの間に配置されている事になる。

② 点Bが点A,Cの間に配置されている

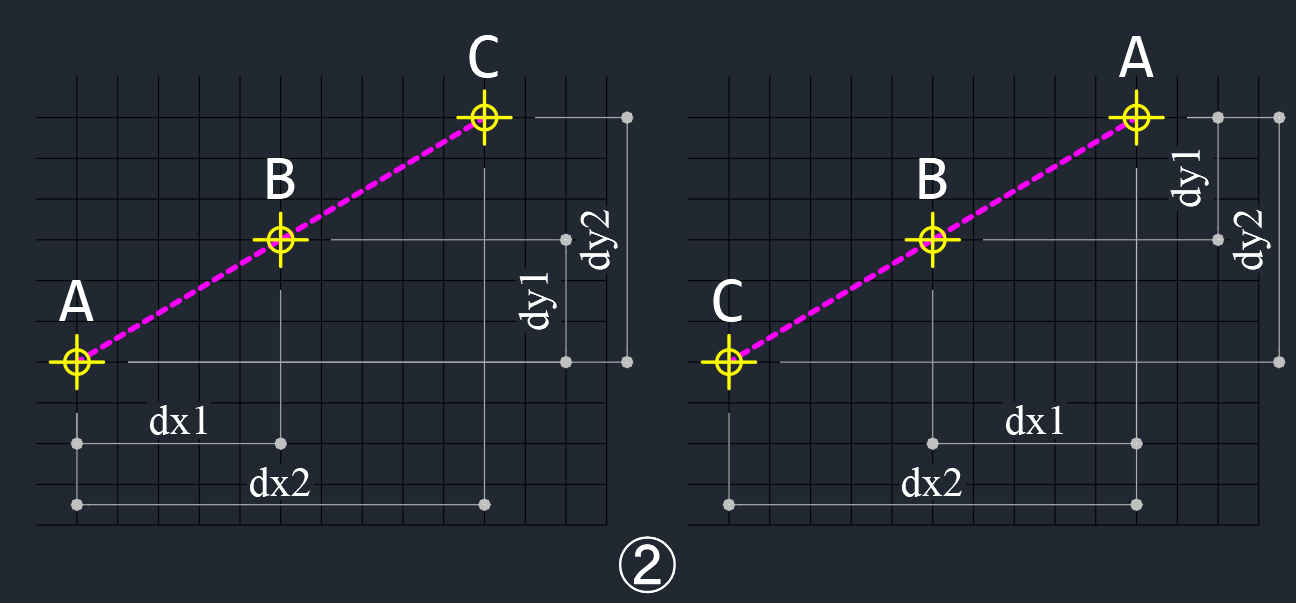
線分ABと線分ACの距離を比較して、線分ABの方が短ければ、点Bが点A,Cの間に配置されている事になる。
2点間の距離、中点の座標を求める
線分ABの距離は、
$ AB = \sqrt{dx1^2 + dy1^2}$
線分ACの距離は、
$ AC = \sqrt{dx2^2 + dy2^2}$
計算を簡単にするために、各距離を二乗して平方根をなくした数を比較する。
ゆえに、
$dx2 \times dy1 = dx1 \times dy2$ かつ、
$ dx1^2 + dy1^2 < dx2^2 + dy2^2$
ならば、点Bが点A,Cの間に配置されている事になる。

③ 点Cが点A,Bの間に配置されている

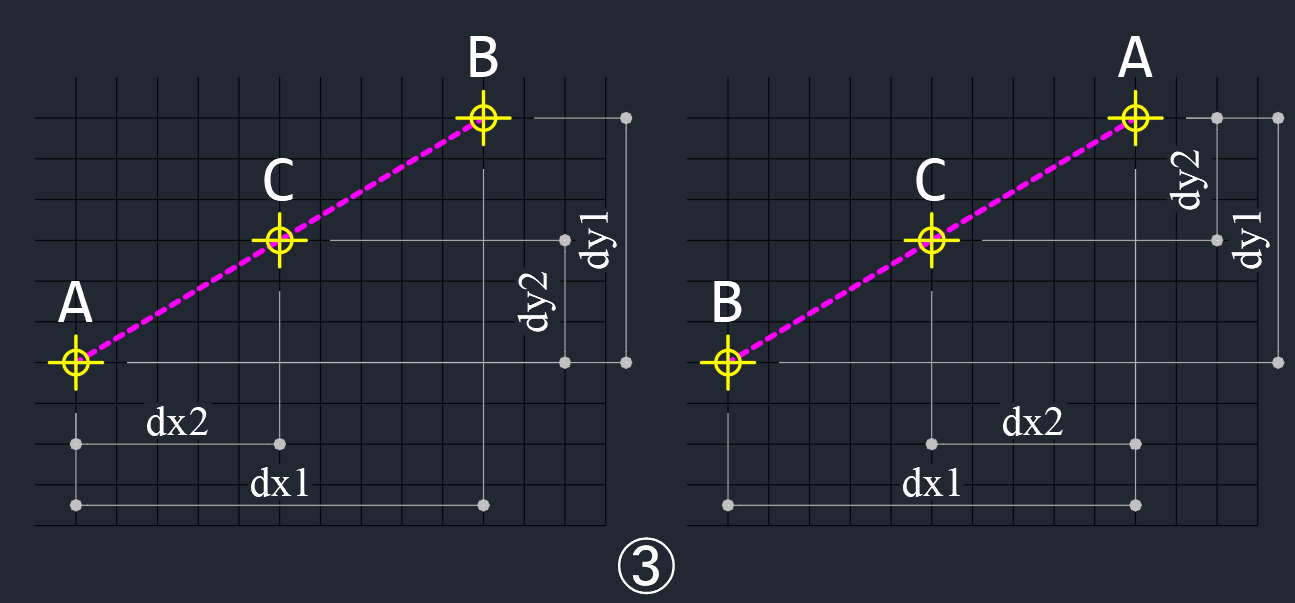
線分ABと線分ACの距離を比較して、線分ACの方が短ければ、点Cが点A,Bの間に配置されている事になる。
（②の逆）
$dx2 \times dy1 = dx1 \times dy2$ かつ、
$ dx1^2 + dy1^2 > dx2^2 + dy2^2$
ならば、点Cが点A,Bの間に配置されている事になる。

もっと簡単な調べ方

3点が同一直線上の点の場合の配置パターンは、

なので、距離を比較して
$ \mid AB \mid + \mid AC \mid = \mid BC \mid $
または、
$ \mid AB \mid + \mid BC \mid = \mid AC \mid $
または、
$ \mid AC \mid + \mid BC \mid = \mid AB \mid $
のいずれかが成り立つ場合、3点は同一直線上の点である。

もっと簡単な調べ方のプログラム

3点が一直線上にあるかどうか調べる
( AutoLISP )

(defun point:IsCollinear (a b c)
    (
        (lambda (ab ac bc)
            (or
                (equal (+ ab ac) bc 1e-8)
                (equal (+ ab bc) ac 1e-8)
                (equal (+ ac bc) ab 1e-8)
            )
        )
        (distance a b) (distance a c) (distance b c)
    )
)
;; < Example >
(point:IsCollinear '(2 3) '(7 6) '(12 9))
;; -> T
(point:IsCollinear '(2 3) '(8 5) '(5 9))
;; -> nil