3点 $A,B,C$ が $A → B → C$ の順に動くときの回転方向を調べる。
調べ方
点Aを基点にして、線分ABと線分ACの傾きを比較する。
- 線分 AB の傾きは $\dfrac{dy1}{dx1}$
- 線分 AC の傾きは $\dfrac{dy2}{dx2}$
線分 AB の傾きのほうが小さいとき、すなわち、
$\dfrac{dy1}{dx1} < \dfrac{dy2}{dx2}$ のとき 左回り。
線分 AB の傾きのほうが大きいとき、すなわち、
$\dfrac{dy1}{dx1} > \dfrac{dy2}{dx2}$ のとき 右回りとなる。
但し、線分AB又はACがY軸に平行な場合、$dx=0$となり、傾きを定義することができないので比べることができない。
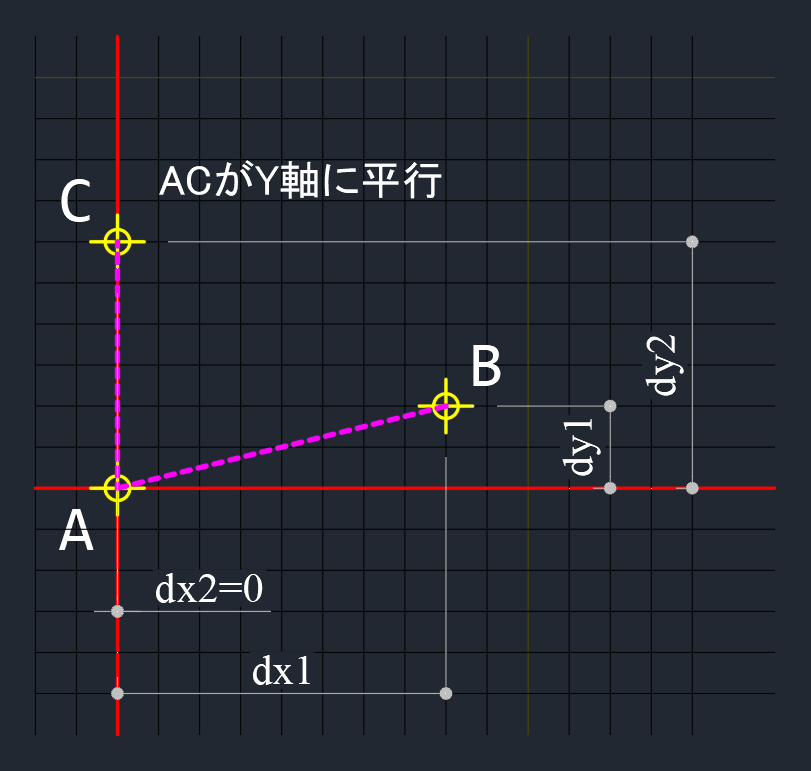これを避けるために、各傾きに $(dx1 \times dx2)$ を掛けた数値を使って比較する。
- 線分 AB の傾き $\dfrac{dy1}{dx1} \times (dx1 \times dx2) = dx2 \times dy1$
- 線分 AC の傾き $\dfrac{dy2}{dx2} \times (dx1 \times dx2) = dx1 \times dy2$
$dx2 \times dy1 < dx1 \times dy2$ ･･･ 左回り（反時計回り）
$dx2 \times dy1 > dx1 \times dy2$ ･･･ 右回り（時計回り）
となる。また、
$dx2 \times dy1 = dx1 \times dy2$ の場合は、
3点は同一直線上の点である。
（3点が同一直線上の点か調べる）
計算例
- $A=(2,3), B=(8,5), C=(5,9)$ のとき
$dx2 \times dy1 = 3 \times 2 = 6$
$dx1 \times dy2 = 6 \times 6 = 36$
$dx2 \times dy1 < dx1 \times dy2$ なので左回り（反時計回り）
プログラム
3点が時計回りに配置されているかどうか調べる
( AutoLISP )
(defun point:IsClockwise (a b c)
(<
(* (- (car b) (car a)) (- (cadr c) (cadr a)))
(* (- (cadr b) (cadr a)) (- (car c) (car a)))
)
)
;; < Example >
(point:IsClockwise '(2 3) '(8 5) '(5 9))
;; -> nil
(point:IsClockwise '(2 3) '(5 9) '(8 5))
;; -> T