交差している状態
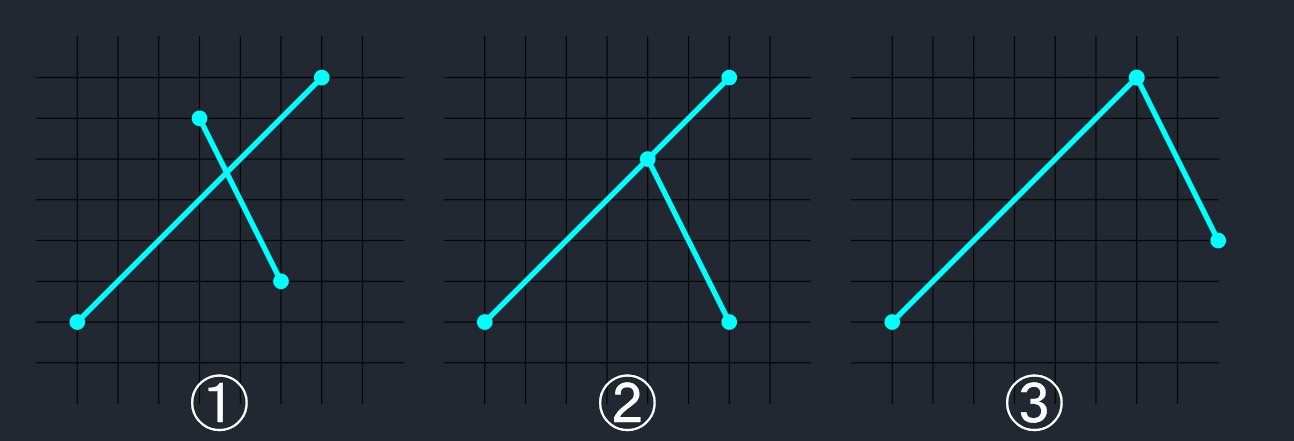
① (明らかに)交差している
② 一方の線分の端点が他方の線分上にある
③ 端点を共有している
交差していない状態
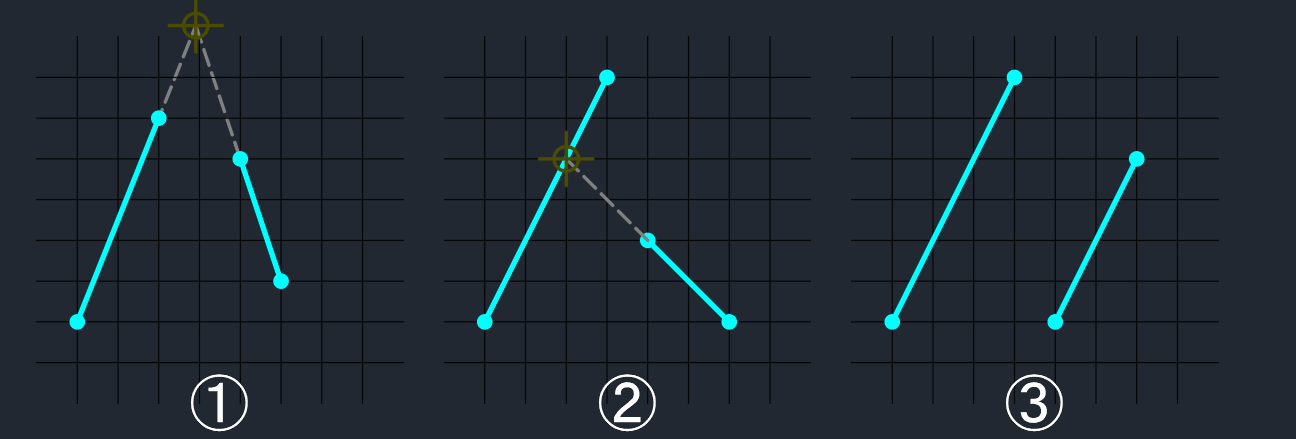
① 線分を含む直線どうしの交点が、線分上にない
② 線分を含む直線どうしの交点が、線分上にある
③ 線分どうしが平行
交差判定の方法
2線分それぞれに対して、他方の線分の両端点がその線分の範囲内でまたいでいる場合交差する。
3点の回転方向を調べる方法を利用して、
線分1の始点 → 線分1の終点 → 線分2の始点 の回転方向と
線分1の始点 → 線分1の終点 → 線分2の終点 の回転方向が逆
かつ、
線分2の始点 → 線分2の終点 → 線分1の始点 の回転方向と
線分2の始点 → 線分2の終点 → 線分1の終点 の回転方向が逆
の場合交差する。
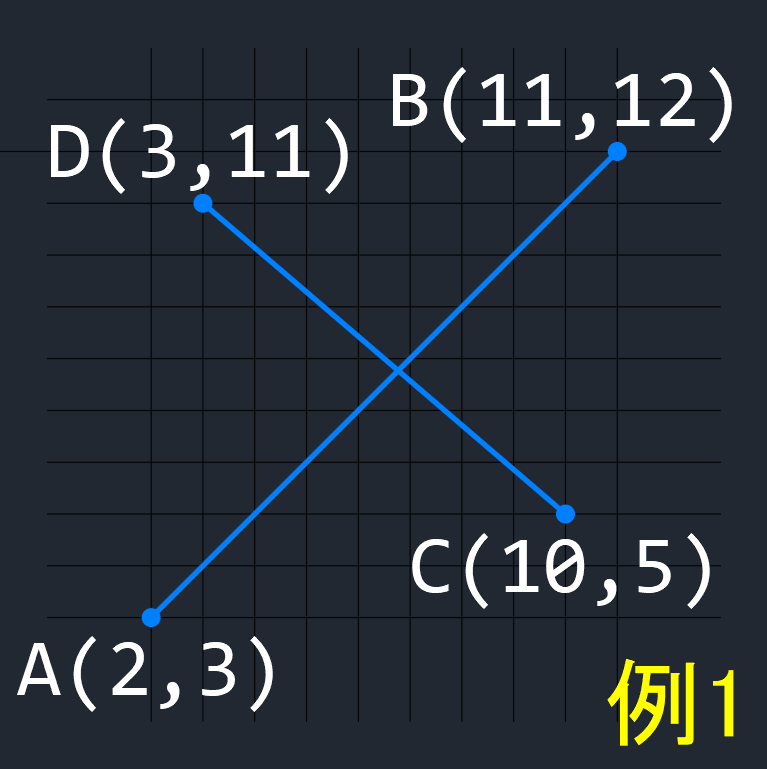
【 例1 】
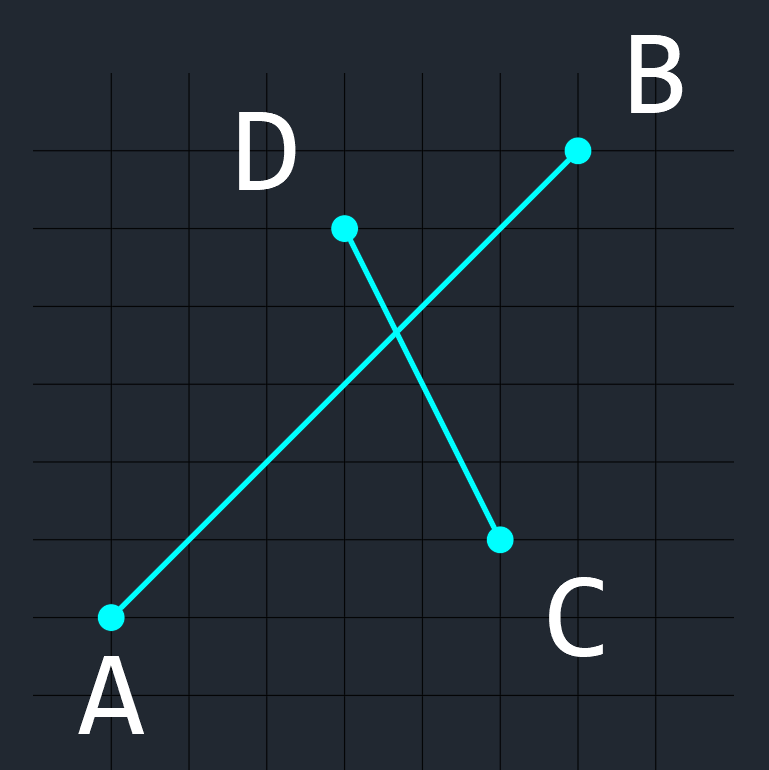
2線分の端点を A,B,C,D とした場合、
A → B → C の回転方向は右回り、
A → B → D の回転方向は左回り(上記と逆)、
C → D → A の回転方向は左回り、
C → D → B の回転方向は右回り(上記と逆)、
なので、この2線分は交差する。
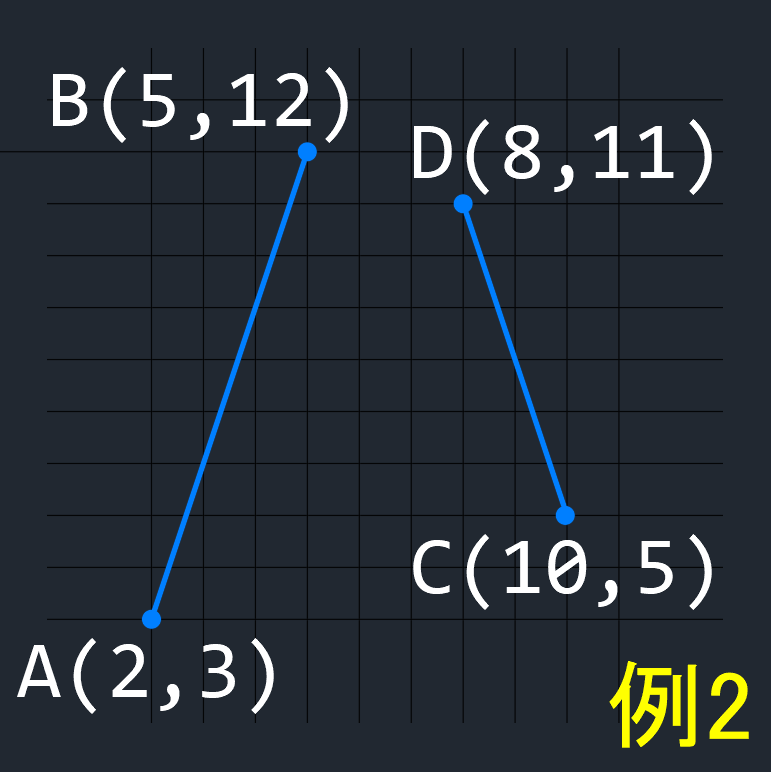
【 例2 】
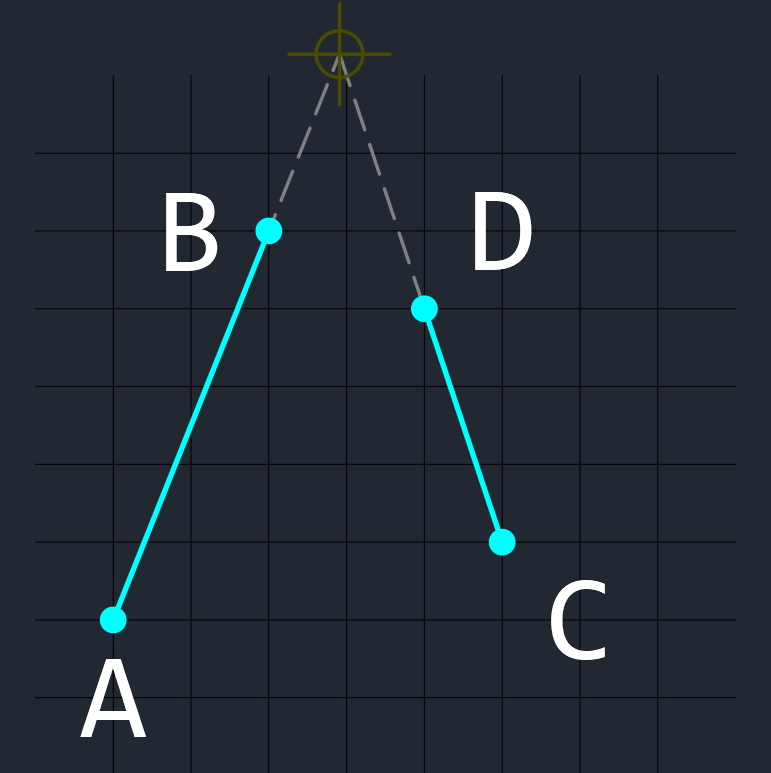
2線分の端点を A,B,C,D とした場合、
A → B → C の回転方向は右回り、
A → B → D の回転方向も右回り(上記と同じ)、
C → D → A の回転方向は左回り、
C → D → B の回転方向も左回り(上記と同じ)、
なので、この2線分は交差しない。
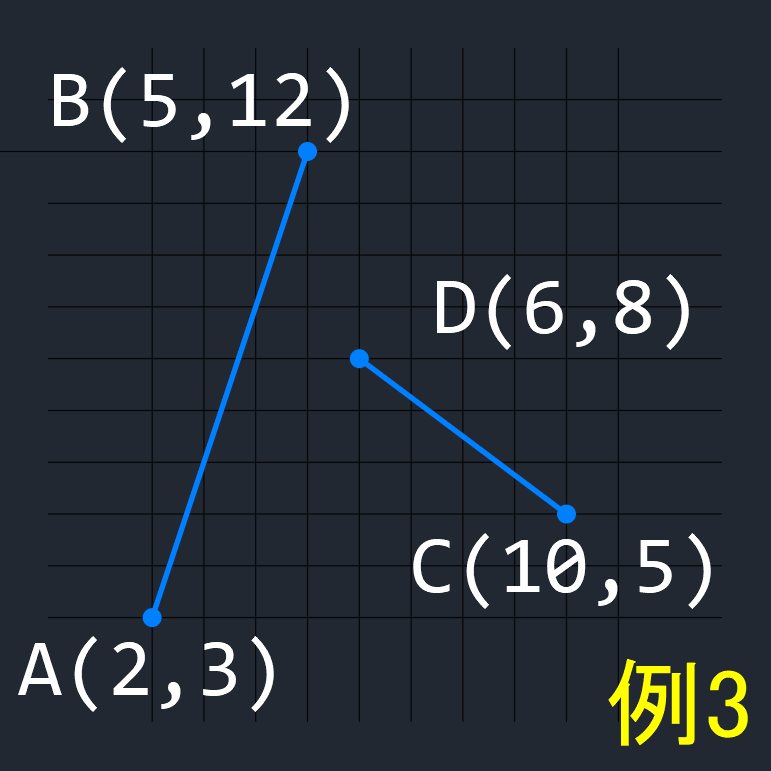
【 例3 】

2線分の端点を A,B,C,D とした場合、
A → B → C の回転方向は右回り、
A → B → D の回転方向も右回り(上記と同じ)、
C → D → A の回転方向は右回り、
C → D → B の回転方向は左回り(上記と逆)、
なので、この2線分は交差しない。
【 例4 】
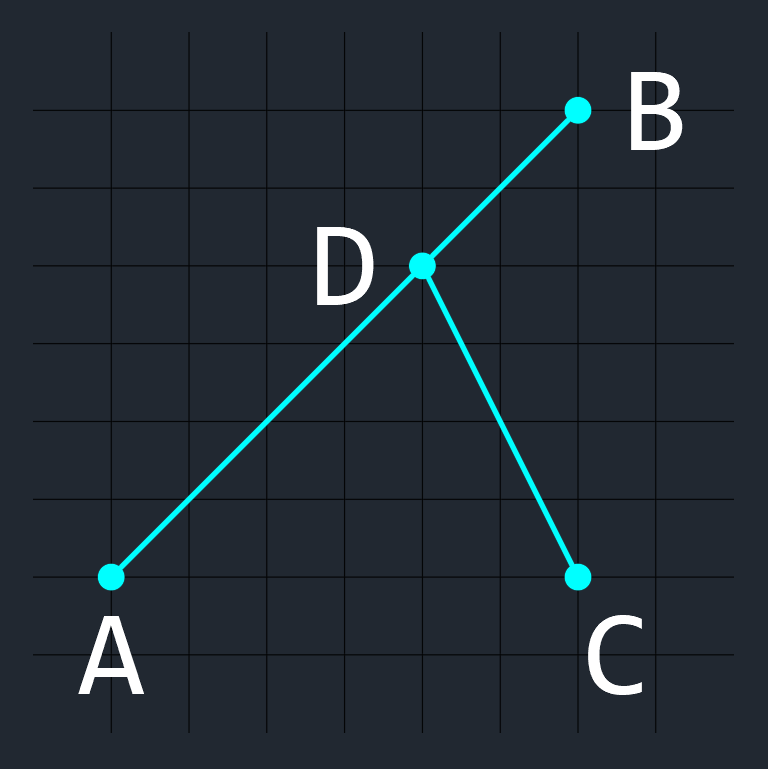
一方の線分の端点が他方の線分上にある場合、
(この場合は、交差していると判定する)
A → B → C の回転方向は右回り、
A → B → D の回転方向はない(同一線上の点なので)、
C → D → A の回転方向は左回り、
C → D → B の回転方向は右回り(上記と逆)、
となり、判定できない。
この場合は、
3点が同一直線上の点か調べるで述べた、3点が同一直線上の点の場合の配置パターンの判定方法を使って、点Dが点A,B間にあるかどうかを調べて判定する。
点A,B,D が同一線上の点の場合、
点Dが点A,Bの間に配置されている場合は交差する。
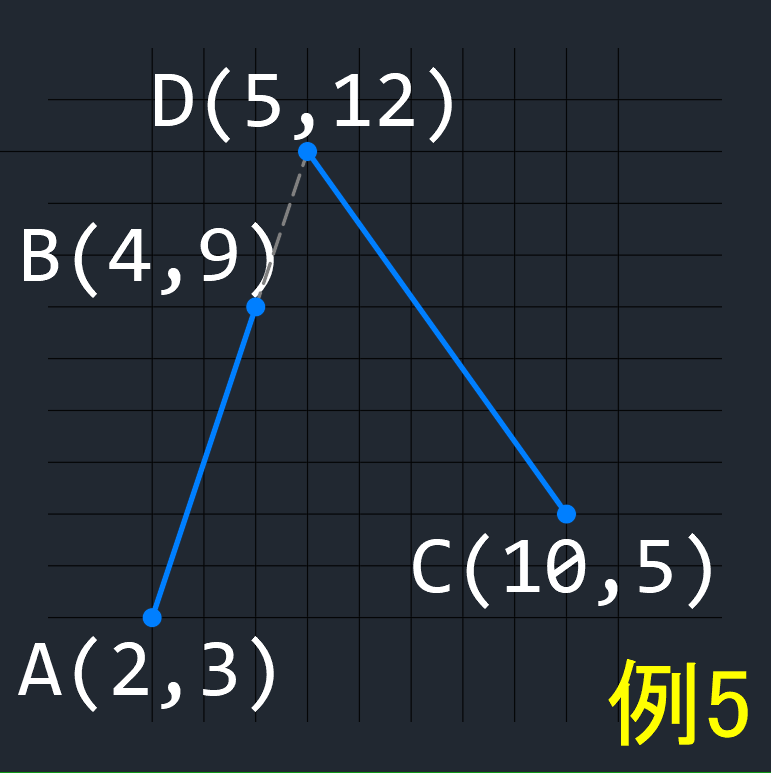
【 例5 】
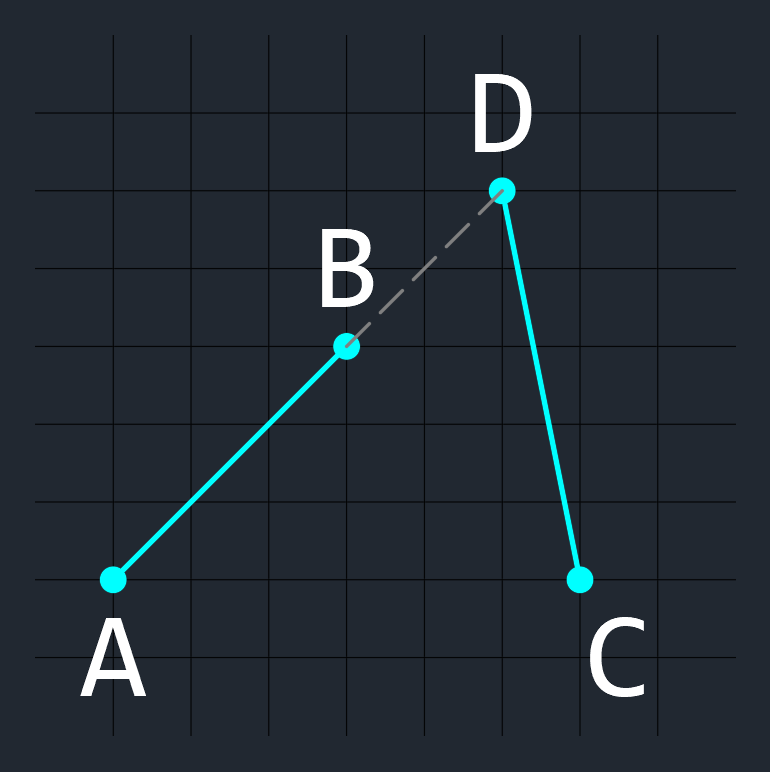
点Dが線分1の延長線上の点の場合、
(この場合は、交差していないと判定する)
A → B → C の回転方向は右回り、
A → B → D の回転方向はない(同一線上の点なので)、
C → D → A の回転方向は左回り、
C → D → B の回転方向は左回り(上記と同じ)、
となり、この2線分は交差しない。
この場合は、
3点が同一直線上の点か調べるで述べた、3点が同一直線上の点の場合の配置パターンの判定方法を使わなくても、判定できる。
【 例6 】
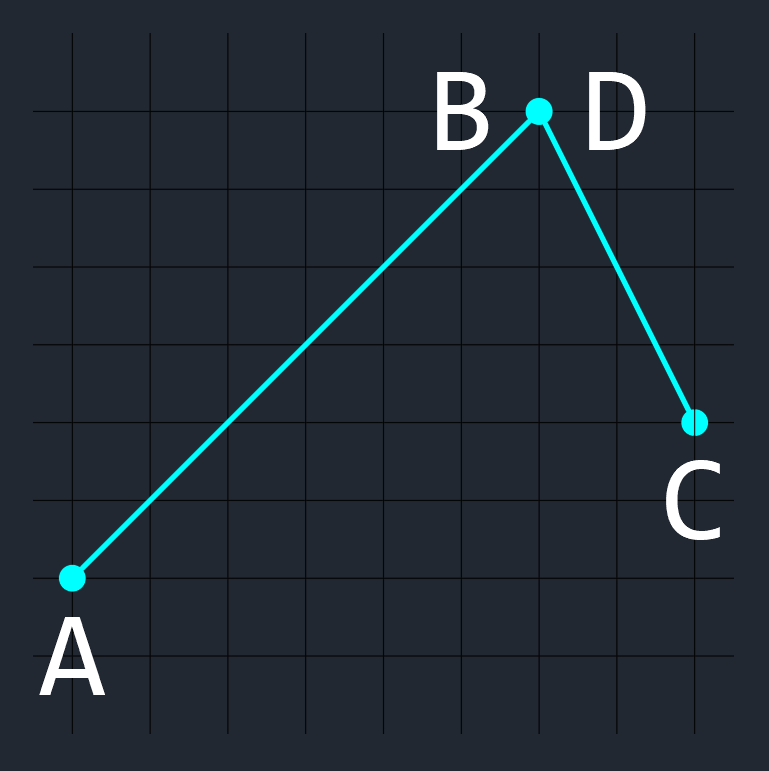
端点を共有している場合(点BとDが同一点)、
(この場合は、交差していると判定する)
A → B → C の回転方向は右回り、
A → B → D の回転方向はない(点BとDが同一点なので)、
C → D → A の回転方向は左回り、
C → D → B の回転方向はない(点BとDが同一点なので)、
となり、判定できない。
この場合も、
3点が同一直線上の点か調べるで述べた、3点が同一直線上の点の場合の配置パターンの判定方法を使って、点Dが点A,B間にあるかどうかまたは、点Bが点C,D間にあるかどうかを調べて判定する。
点B,D が同一点の場合、
点Dが点A,Bの間に配置されている
または、
点Bが点C,Dの間に配置されている場合は交差する。
交差判定プログラム
3点の回転方向を調べる方法と
3点が同一直線上の点か調べるの3点が同一直線上の点の場合の配置パターンの判定方法を使って、次のような "3点の回転方向を調べる" 関数を作成する。
- 右回り(反時計回り)のとき、1
- 左回り(時計回り)のとき、-1
- 3点が同一線上の点の場合
- 点Aが点BとCの間のとき、-1
- 点Bが点AとCの間のとき、1
- 点Cが点AとBの間のとき、0
を返す関数。
3点の回転方向を調べる
( AutoLISP )
(defun point:GetDirectionRotation (a b c / dx1 dx2 dy1 dy2)
(setq dx1 (- (car b) (car a))
dy1 (- (cadr b) (cadr a))
dx2 (- (car c) (car a))
dy2 (- (cadr c) (cadr a))
)
(cond
((< (* dx2 dy1) (* dx1 dy2)) 1)
((> (* dx2 dy1) (* dx1 dy2)) -1)
((or (< (* dx1 dx2) 0) (< (* dy1 dy2) 0)) -1)
((< (+ (* dx1 dx1) (* dy1 dy1)) (+ (* dx2 dx2) (* dy2 dy2))) 1)
(T 0)
)
)
;; < Example >
;; (point:GetDirectionRotation '(2 3) '(8 5) '(5 9)) -> 1
;; (point:GetDirectionRotation '(2 3) '(5 9) '(8 5)) -> -1
;; (point:GetDirectionRotation '(7 6) '(2 3) '(12 9)) -> -1
;; (point:GetDirectionRotation '(2 3) '(7 6) '(12 9)) -> 1
;; (point:GetDirectionRotation '(2 3) '(12 9) '(7 6)) -> 0
この関数を利用して、交差判定のプログラムを次のように定義する。
2線分の交差判定
( AutoLISP )
(defun lineSeg:IsIntersect (line1 line2)
(and
(<=
(*
(point:GetDirectionRotation (car line1) (cadr line1) (car line2))
(point:GetDirectionRotation (car line1) (cadr line1) (cadr line2))
)
0
)
(<=
(*
(point:GetDirectionRotation (car line2) (cadr line2) (car line1))
(point:GetDirectionRotation (car line2) (cadr line2) (cadr line1))
)
0
)
)
)
;; < Example >
;; 例1 (lineSeg:IsIntersect '((2 3) (11 12)) '((10 5) (3 11))) -> T
;; 例2 (lineSeg:IsIntersect '((2 3) (5 12)) '((10 5) (8 11))) -> nil
;; 例3 (lineSeg:IsIntersect '((2 3) (5 12)) '((10 5) (6 8))) -> nil
;; 例4 (lineSeg:IsIntersect '((2 3) (11 12)) '((10 5) (8 9))) -> T
;; 例5 (lineSeg:IsIntersect '((2 3) (4 9)) '((10 5) (5 12))) -> nil
;; 例6 (lineSeg:IsIntersect '((2 3) (7 12)) '((10 5) (7 12))) -> T