円と直線の位置関係
円と直線の位置関係は
- 異なる２点で交わる
- １点で接する
- 共有点を持たない
のいずれか。
円と直線の関係の判定方法
円の中心から直線までの距離と円の半径を比較して判定する。
（点と直線の距離）
円の半径を $r$ 、円の中心から直線までの距離を $d$ とすると、
- $d>r$ ならば、異なる２点で交わる
- $d=r$ ならば、１点で接する
- $d<r$ ならば、共有点を持たない
異なる２点で交わる場合の交点の求め方の考え方
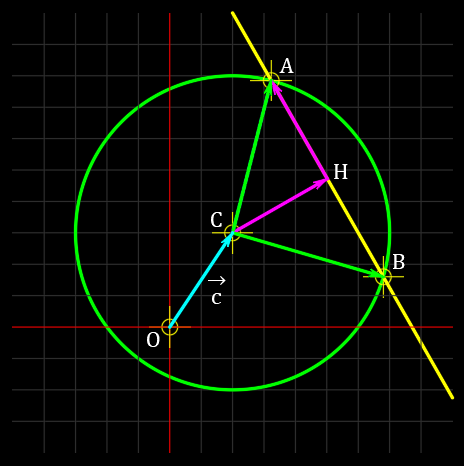円の中心を $C$ 、２つの交点を $A,B$、点 $C$ から直線に向かって下ろした垂線と直線との交点を $H$ とすると、
点 $C$ から点 $A$ に向かうベクトルは、
$$\overrightarrow{CA}=\overrightarrow{CH}+\overrightarrow{HA}$$
となる。
よって、点 $A$ の座標は、点 $C$ の位置ベクトルを $\vec{c}$ とすると、
$$A=\vec{c}+\overrightarrow{CA}$$
で求める事ができる。
点 $C$ から点 $B$ に向かうベクトルは、
$$\overrightarrow{CB}=\overrightarrow{CH}-\overrightarrow{HA}$$
となる。
よって、点 $B$ の座標は、点 $C$ の位置ベクトルを $\vec{c}$ とすると、
$$B=\vec{c}+\overrightarrow{CB}$$
で求める事ができる。
異なる２点で交わる場合の交点の求め方
中心の座標が $(x_0,y_0)$ 半径 $r$ の円 $(x-x_0)^2+(y-y_0)^2=r^2$と、直線 $ax+by+c=0$ の交点を求める。
上記求め方の考え方により、まずベクトル $\overrightarrow{CH}, \overrightarrow{HA}$ を求める必要がある。
$\overrightarrow{CH}$ を求めるには、直線の法線ベクトル $\vec{n}$ の単位ベクトルに、点 $C$ から 点 $H$ までの距離 $s$ を掛けることで求める事ができる。
$\overrightarrow{HA}$ を求めるには、直線の方向ベクトル $\vec{d}$ の単位ベクトルに、点 $H$ から 点 $A$ までの距離 $t$ を掛けることで求める事ができる。
直線 $ax+by+c=0$ の法線ベクトル $\vec{n}$、方向ベクトル $\vec{d}$ はそれぞれ、
$$\vec{n}=(a,b) \ \ \ \ \ \ , \ \ \ \ \vec{d}=(-b,a)$$
となる。（直線のベクトル方程式 参照）
$\vec{n},\vec{d}$ の単位ベクトルは、$a,b$ の距離の逆数
$$\frac{1}{\sqrt{a^2+b^2}}$$
を掛けることで求める事ができる。
$\vec{n}$ の単位ベクトルを $\vec{h}$ とすると、
$$\vec{h}=\vec{n}\cdot\frac{1}{\sqrt{a^2+b^2}}=(a,b)\cdot\frac{1}{\sqrt{a^2+b^2}}=\left(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}\right) \ \cdots \ ①$$
となる。
$\vec{d}$ の単位ベクトルを $\vec{k}$ とすると、
$$\vec{k}=\vec{d}\cdot\frac{1}{\sqrt{a^2+b^2}}=(-b,a)\cdot\frac{1}{\sqrt{a^2+b^2}}=\left(-\frac{b}{\sqrt{a^2+b^2}},\frac{a}{\sqrt{a^2+b^2}}\right) \ \cdots \ ②$$
となる。
距離 $s$ は、 点と直線の距離の公式により、
$$s=\dfrac{\mid ax_0+by_0+c\mid}{\sqrt{a^2+b^2}}$$
$D=\mid ax_0+by_0+c\mid$ とおくと、（以降の計算で式が長くなるので）
$$s=\dfrac{D}{\sqrt{a^2+b^2}} \ \cdots \ ③$$
となる。
距離 $t$ は、三平方の定理より $r^2=s^2+t^2\ \dashrightarrow \ t^2=r^2-s^2$ よって、
$$t=\sqrt{r^2-s^2}$$
この式に上記の$s$の式を代入すると、
$$t=\sqrt{r^2-\left(\frac{D}{\sqrt{a^2+b^2}}\right)^2}=\sqrt{r^2-\frac{D^2}{a^2+b^2}}=\frac{\sqrt{(a^2+b^2)r^2-D^2}}{\sqrt{a^2+b^2}} \ \cdots \ ④$$
式①、③により$\overrightarrow{CH}$は
$$\overrightarrow{CH}=s\vec{h}=\dfrac{D}{\sqrt{a^2+b^2}}\cdot\left(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}\right)=\left(\frac{aD}{a^2+b^2},\frac{bD}{a^2+b^2}\right)$$
式②、④により$\overrightarrow{HA}$は
$$\overrightarrow{HA}=t\vec{k}=\frac{\sqrt{(a^2+b^2)r^2-D^2}}{\sqrt{a^2+b^2}}\cdot\left(-\frac{b}{\sqrt{a^2+b^2}},\frac{a}{\sqrt{a^2+b^2}}\right)$$
$$=\left(-\frac{b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)$$
ゆえに、
$\overrightarrow{CA}=\overrightarrow{CH}+\overrightarrow{HA}$ より、
$$\overrightarrow{CA}=\left(\frac{aD}{a^2+b^2},\frac{bD}{a^2+b^2}\right)+\left(-\frac{b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)$$
$$=\left(\frac{aD-b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{bD+a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)ただし、D=\mid ax_0+by_0+c\mid$$
$\overrightarrow{CB}=\overrightarrow{CH}-\overrightarrow{HA}$ より、
$$\overrightarrow{CB}=\left(\frac{aD}{a^2+b^2},\frac{bD}{a^2+b^2}\right)-\left(-\frac{b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)$$
$$=\left(\frac{aD+b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{bD-a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)ただし、D=\mid ax_0+by_0+c\mid$$
よって、点 $A$ の座標は、
$$A=\vec{c}+\overrightarrow{CA}=(x_0,y_0)+\left(\frac{aD-b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{bD+a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)$$
$$=\left(\frac{aD-b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+x_0,\frac{bD+a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+y_0\right)$$
$$ただし、D=\mid ax_0+by_0+c\mid$$
点 $B$ の座標は、
$$B=\vec{c}+\overrightarrow{CB}=(x_0,y_0)+\left(\frac{aD+b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2},\frac{bD-a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}\right)$$
$$=\left(\frac{aD+b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+x_0,\frac{bD-a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+y_0\right)$$
$$ただし、D=\mid ax_0+by_0+c\mid$$
で求めることができる。
また、直線 $ax+by+=0$ が正規化されている場合は、（直線の方程式を正規化する 参照）
$$A=\left(aD-b\sqrt{r^2-D^2}+x_0,bD+a\sqrt{r^2-D^2}+y_0\right)$$
$$B=\left(aD+b\sqrt{r^2-D^2}+x_0,bD-a\sqrt{r^2-D^2}+y_0\right)$$
$$ただし、D=\mid ax_0+by_0+c\mid$$
となる。
【例】中心(3,2) 半径 5 の円と、直線 3x+2y-16=0 の交点を求める
まず $D$ を求める
$$D=\mid ax_0+by_0+c\mid=\mid 3\cdot3+2\cdot2-16\mid=\mid-3\mid=3$$
点 $A$ の $x$ 座標を求める
$$x_A=\frac{aD-b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+x_0=\frac{3\cdot3-2\sqrt{(3^2+2^2)5^2-3^2}}{3^2+2^2}+3$$
$$=\frac{9-2\sqrt{316}}{13}+3=\frac{48-4\sqrt{79}}{13}\fallingdotseq 0.957479$$
点 $A$ の $y$ 座標を求める
$$y_A=\frac{bD+a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+y_0=\frac{2\cdot3+3\sqrt{(3^2+2^2)5^2-3^2}}{3^2+2^2}+2$$
$$=\frac{6+3\sqrt{316}}{13}+2=\frac{32+6\sqrt{79}}{13}\fallingdotseq 6.563782$$
点 $B$ の $x$ 座標を求める
$$x_B=\frac{aD+b\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+x_0=\frac{3\cdot3+2\sqrt{(3^2+2^2)5^2-3^2}}{3^2+2^2}+3$$
$$=\frac{9+2\sqrt{316}}{13}+3=\frac{48+4\sqrt{79}}{13}\fallingdotseq 6.427137$$
点 $B$ の $y$ 座標を求める
$$y_B=\frac{bD-a\sqrt{(a^2+b^2)r^2-D^2}}{a^2+b^2}+y_0=\frac{2\cdot3-3\sqrt{(3^2+2^2)5^2-3^2}}{3^2+2^2}+2$$
$$=\frac{6-3\sqrt{316}}{13}+2=\frac{32-6\sqrt{79}}{13}\fallingdotseq -1.640705$$
したがって、
$$A=\left(\frac{48-4\sqrt{79}}{13}, \frac{32+6\sqrt{79}}{13} \right)\fallingdotseq (0.957479,6.563782)$$
$$B=\left(\frac{48+4\sqrt{79}}{13}, \frac{32-6\sqrt{79}}{13} \right)\fallingdotseq (6.427137,-1.640705)$$
となる。
１点で接する場合の交点の求め方
このときの交点を円と直線の接点、直線を円の接線という。
中心の座標が $(x_0,y_0)$ 半径 $r$ の円と、直線 $ax+by+c=0$ の位置関係が１点で接するとして、その接点 $H$ の座標を求める。
点 $H$ の座標は、点 $C$ の位置ベクトルを $\vec{c}$ とすると、
$$H=\vec{c}+\overrightarrow{CH}$$
となる。
$\overrightarrow{CH}$ を求めるには、直線の法線ベクトル $\vec{n}$ の単位ベクトルに、点 $C$ から 点 $H$ までの距離 $r$ すなわち、円の半径を掛けることで求める事ができる。
直線 $ax+by+c=0$ の法線ベクトル $\vec{n}$ は、
$$\vec{n}=(a,b)$$
（直線のベクトル方程式 参照）
$\vec{n}$ の単位ベクトル $\vec{h}$ は上記 式①により、
$$\vec{h}=\vec{n}\cdot\frac{1}{\sqrt{a^2+b^2}}=(a,b)\cdot\frac{1}{\sqrt{a^2+b^2}}=\left(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}\right) \ \cdots \ ①$$
となる。
これにより$\overrightarrow{CH}$は
$$\overrightarrow{CH}=r\vec{h}=r\cdot\left(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}\right)=\left(\frac{ar}{\sqrt{a^2+b^2}},\frac{br}{\sqrt{a^2+b^2}}\right)$$
となる。
したがって、点 $H$ の座標は
$$H=\vec{c}+\overrightarrow{CH}=(x_0,y_0)+\left(\frac{ar}{\sqrt{a^2+b^2}},\frac{br}{\sqrt{a^2+b^2}}\right)=\left(\frac{ar}{\sqrt{a^2+b^2}}+x_0,\frac{br}{\sqrt{a^2+b^2}}+y_0\right)$$
で求める事ができる。