2直線の垂直条件を利用して求める
直線 $ax+by+c=0$ と直線上にない点 $P(x_0,y_0)$ との距離を求める。
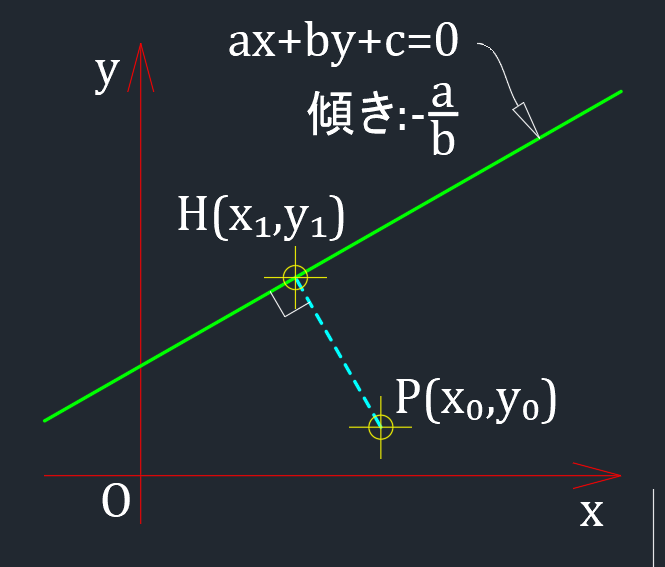
$P$ から直線に垂直に下ろした線を $PH$ とする。
$a\neq0,b\neq0$ とし、直線と点 $P$ との交点 $H$ の座標を $(x_1,y_1)$ とすると、
直線 $PH$ の傾きは $\dfrac{y_1-y_0}{x_1-x_0}$、距離は $\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}$ となる。
一方、直線 $ax+by+c=0$ の傾きは、 $-\dfrac{a}{b}$ で、(直線の方程式 参照)
直線と $PH$ は垂直なので、その積は、
$$\dfrac{y_1-y_0}{x_1-x_0}\cdot -\dfrac{a}{b}=-1$$
となる。(平行な直線と垂直な直線 参照)
この式を変形すると、
$$\dfrac{a(y_1-y_0)}{b(x_1-x_0)}=1\ \dashrightarrow \ b(x_1-x_0)=a(y_1-y_0)\ \dashrightarrow \ \dfrac{b(x_1-x_0)}{ab}=\dfrac{a(y_1-y_0)}{ab}$$
となり、
$$\dfrac{x_1-x_0}{a}=\dfrac{y_1-y_0}{b}$$
となる。この値を $k$ とおくと、
$$\dfrac{x_1-x_0}{a}=k \ , \ \dfrac{y_1-y_0}{b}=k$$
$$x_1-x_0=ak \ , \ y_1-y_0=bk \ \cdots \ ①$$
となる。
この式を、$PH$ の距離の式の両辺を二乗した $PH^2=(x_1-x_0)^2+(y_1-y_0)^2$ に代入すると、
$$PH^2=(ak)^2+(bk)^2=a^2k^2+b^2k^2=(a^2+b^2)k^2 \ \cdots \ ②$$
①の式を変形すると、
$$x_1=x_0+ak \ , \ y_1=y_0+bk \ \cdots \ ③$$
点 $H(x_1,y_1)$ は直線 $ax+by+c=0$ 上の点なので、
$$ax_1+by_1+c=0$$
が成り立つ。
この式に③の値を代入すると、
$$a(x_0+ak)+b(y_0+bk)+c=0$$
この式を $k$ について解くと、
$ax_0+a^2k+by_0+b^2k+c=0\ \dashrightarrow \ k(a^2+b^2)=-(ax_0+by_0+c)$
$$k=-\dfrac{ax_0+by_0+c}{a^2+b^2}$$
となる。
この $k$ の式を②に代入すると、
$$PH^2=(a^2+b^2)k^2=(a^2+b^2)\cdot \left(-\dfrac{ax_0+by_0+c}{a^2+b^2}\right)^2$$
$$=\dfrac{(a^2+b^2)\cdot (ax_0+by_0+c)^2}{(a^2+b^2)^2}=\dfrac{(ax_0+by_0+c)^2}{a^2+b^2}$$
ゆえに、
$$PH=\dfrac{\mid ax_0+by_0+c\mid}{\sqrt{a^2+b^2}} \ \cdots \ ④$$
これが直線 $ax+by+c=0$ と直線上にない点 $(x_0,y_0)$ との距離の公式です。
この公式は $a=0$ または $b=0$ のときも成り立つ。
$a=0$ のとき、直線 $ax+by+c=0$ は $by+c=0$ となり、
$$y=-\frac{c}{b}$$
となる。これは $x$軸に平行な直線を表す。
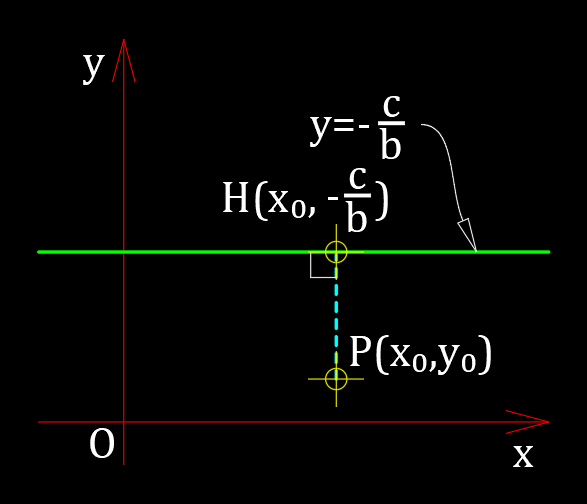
このとき、点$P(x_0,y_0)$ とこの直線との距離は、
$$\left|\ y_0-\left(-\frac{c}{b}\right)\right|$$
この式は、④の式で $a=0$ にした場合、
$$PH=\dfrac{\mid by_0+c\mid}{b}$$
と同じ式となり、$a=0$ の場合も成り立つといえる。
$b=0$ のとき、直線 $ax+by+c=0$ は $ax+c=0$ となり、
$$x=-\frac{c}{a}$$
となる。これは $y$軸に平行な直線を表す。
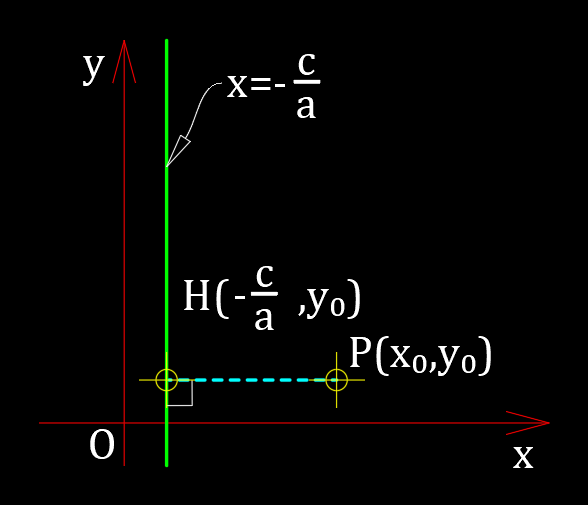
このとき、点$P(x_0,y_0)$ とこの直線との距離は、
$$\left|\ x_0-\left(-\frac{c}{a}\right)\right|$$
この式は、④の式で $b=0$ にした場合、
$$PH=\dfrac{\mid ax_0+c\mid}{a}$$
と同じ式となり、$b=0$ の場合も成り立つといえる。
また、原点 $(0,0)$ と直線 $ax+by+c=0$との距離は、
$$PH=\dfrac{\mid c\mid}{\sqrt{a^2+b^2}}$$
です。