Julia早引きノート［16］集合

###集合(書き方例)

note16

# 初期化時に要素を指定
set1 = Set([1,2,3,4,5,])

# 空集合で初期化
set2 = Set()

# 要素の追加(単要素)
push!(set2, 4)

# 要素の追加(複数要素)
push!(set2, 5, 6, 7)

# 要素の削除
pop!(set2, 7)

◆集合の演算
　# 和集合
　union(set1, set2)
　∪(set1, set2)
　set1 ∪ set2

　# 積集合
　intersect(set1, set2)
　∩(set1, set2)
　set1 ∩ set2

　# 差集合
　setdiff(set1, set2)

　# 対照差(symdiff)
　symdiff(set1, set2)

　# 部分集合の判定
　issubset(set1, set2)
　⊆(set1, set2)
　⊇(set1, set2)
　set1 ⊆ set2
　set1 ⊇ set2

　# 集合が等しいか判定
　issetequal(set1, set2)

◆その他の関数
　# 空かどうかの判定
　isempty(set1)
　# 要素数取得
　length(set1)
　# 空にする
　empty!(set1)

##解説
・キーのみからなる要素が重複なく格納されているコレクション。
・同じキーの要素を追加してもエラーにならないが、重複は許されないため、要素数は増えない。
・以下のように空集合を宣言すると要素がAny型となり、どんな型でも格納することができます。
　集合名 = Set()
・集合の中の要素には順序性は保証されません。
・和集合、差集合、積集合など集合用の特別な演算を用いて、異なる集合間で共通する要素や、要素同士の差異など、関係性を比較するのに便利です。
・演算の結果、得られる値は集合です。

####①和集合(union, ∪)
2つの集合のすべての要素を取得します。

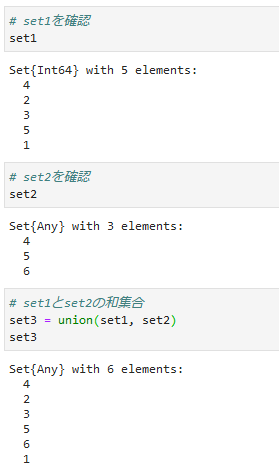
**集合の記号[∪]**も使用できます。

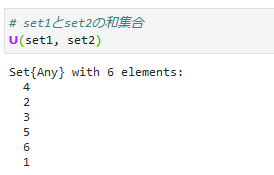
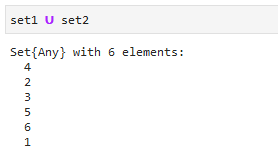
また、通常の比較演算子としても使用できます。

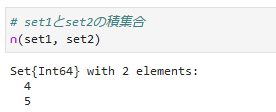
####②積集合(intersect, ∩)
2つの集合間で共通に含まれる要素を取得します。

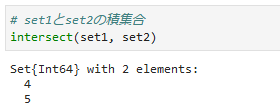
**集合の記号[∩]**も使用できます。

また、通常の比較演算子としても使用できます。

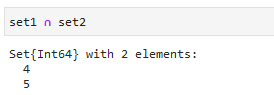
####③差集合(setdiff)
2つの集合の差を取得します。第一引数の集合から第二引数の集合を引いた要素を返します。

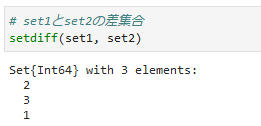
####④対照差(symdiff)
2つの集合のどちらか一方だけに含まれる要素を取得します。

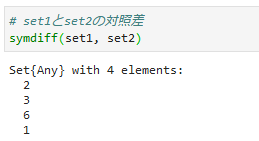
####⑤部分集合(issubset, ⊆, ⊇)
issubset(A, B)は、AがBの部分集合であるかどうかを判定します。結果はtrue/falseが返ります。

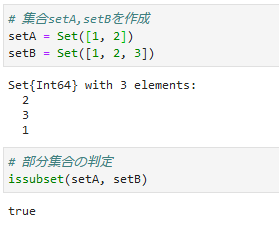
同様に、**部分集合の記号[⊆],[⊇]**も使用できます。

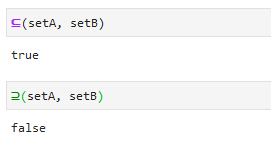
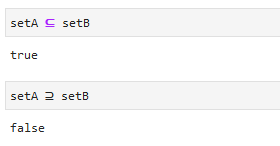
また、通常の比較演算子としても使用できます。

####⑥集合が等しいか判定(issetequal)
2つの集合が同じものであるかどうかを判定します。

####◆その他の関数

isempty()

空かどうかを判定します。true/falseを返します。

length()

要素数を取得します。

empty!()

要素を削除し、空にします。

##もくじ
Julia早引きノート［01］変数・定数の使い方
Julia早引きノート［02］算術式、演算子
[Julia早引きノート［03］複素数]
(https://qiita.com/ttabata/items/225c77a4d71fafc3e482)
Julia早引きノート［04］正規表現
....

もくじを開く

[Julia早引きノート［05］if文] (https://qiita.com/ttabata/items/4f0bcff1e32f60402dfb) [Julia早引きノート［06］ループ処理] (https://qiita.com/ttabata/items/2a53825101b0b75fb589) [Julia早引きノート［07］try, catch, finally] (https://qiita.com/ttabata/items/1d6fe990526c99b65b5f) [Julia早引きノート［08］変数の型(Int, Float, Bool, Char, String)] (https://qiita.com/ttabata/items/2b84a826e39bfe432b62) [Julia早引きノート［09］関数 (1)基本編] (https://qiita.com/ttabata/items/d9b4f2728ec0dbcc6394) [Julia早引きノート［10］関数 (2)応用編] (https://qiita.com/ttabata/items/462e216c43d519f1969d) [Julia早引きノート［11］Nothing型] (https://qiita.com/ttabata/items/0e5a6b21968d8752cf0b) [Julia早引きノート［12］複合型(Composite Type)型] (https://qiita.com/ttabata/items/27469216a3c33101c825) [Julia早引きノート［13］タプル] (https://qiita.com/ttabata/items/ebe35dbfec4efbc1c29a) [Julia早引きノート［14］リスト(Array型一次元配列)] (https://qiita.com/ttabata/items/7528863ccbb282e8260d) [Julia早引きノート［15］辞書(dictionary)] (https://qiita.com/ttabata/items/77a4f1d02b51d067bfb7) [Julia早引きノート［16］集合] (https://qiita.com/ttabata/items/ca8137922a785122037e) [Julia早引きノート［17］多次元配列 (1)初期化] (https://qiita.com/ttabata/items/01fecbd14363460a27a6) [Julia早引きノート［18］多次元配列 (2)様々な演算や関数] (https://qiita.com/ttabata/items/f35896a5fa005fba7fbc) [Julia早引きノート［19］多次元配列 (3)サブ配列] (https://qiita.com/ttabata/items/045c00406fe45270b42e) [Julia早引きノート［20］ファイル入出力] (https://qiita.com/ttabata/items/5a99c3998060d161ace8) [Julia早引きノート［21］JSON、XMLファイルの入出力] (https://qiita.com/ttabata/items/65ebec11830271f9be71) [Julia早引きノート［22］Python関数やPythonモジュールの呼び出し] (https://qiita.com/ttabata/items/3afc8cef40d1e98a7b17) [Julia早引きノート［23］JuliaでのMatplotlibによるグラフ描画] (https://qiita.com/ttabata/items/96a0e172addfac690cca) [Julia早引きノート［24］CSVFiles(DataFrameとの連携)] (https://qiita.com/ttabata/items/51446731a703b5aca524) [Julia早引きノート［25］線形代数演算(ベクトル・行列計算)] (https://qiita.com/ttabata/items/5abe14d5c510e8ca0f54) (※引き続きコンテンツを増やしていきます)

##関連情報

Julia - 公式ページ
https://julialang.org/

Julia - 日本語公式ドキュメント
https://julia-doc-ja.readthedocs.io/ja/latest/index.html

初めてのJuliaとインストール (Windows & Linux)
https://qiita.com/ttlabo/items/b05bb43d06239f968035

Julia - Mathematics
https://docs.julialang.org/en/v1/base/math/

##ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。