###線形代数演算(ベクトル・行列計算)(書き方例)
◆LinearAlgebraモジュールの読み込み
using LinearAlgebra
◆ベクトルの演算
# 内積(2つのベクトルをa,bとする)
dot(a, b)
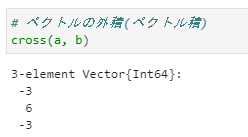
# 外積(ベクトル積)
cross(a, b)
# L1ノルム(vを求める対象のベクトルとする)
norm(v, 1)
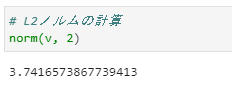
# L2ノルム
norm(v, 2)
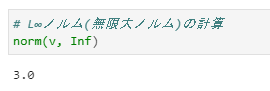
# L∞ノルム(無限大ノルム)
norm(v, Inf)
# L1ノルムでの正規化
normalize(v, 1)
# L2ノルムでの正規化
normalize(v, 2)
◆行列の演算
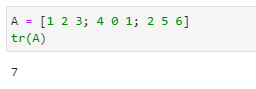
# トレース(求める対象の行列をAとする)
tr(A)
# 行列式
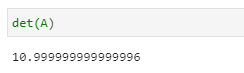
det(A)
# 逆行列
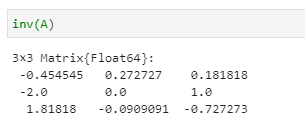
inv(A)
# 対称行列
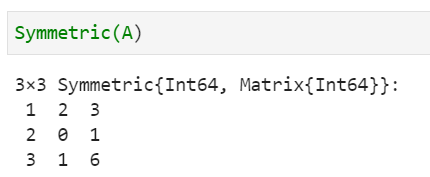
Symmetric(A)
# エルミート行列
Hermitian(A)
# 上三角行列
UpperTriangular(A)
# 下三角行列
LowerTriangular(A)
# 対角行列
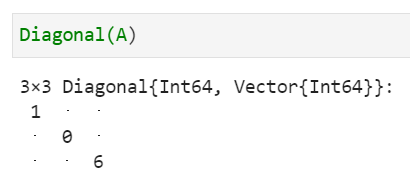
Diagonal(A)
# 転置行列
transpose(A)
##解説
Juliaでは、標準ライブラリに含まれているLinearAlgebraモジュールを使用することで、線形代数の計算や、定型的な行列を求めるなど、便利な機能を使用することができます。
・実際の計算を行う前に、以下のコマンドでLinearAlgebraモジュールを読み込んでおく必要があります。
using LinearAlgebra
・ベクトルに関しては、内積、外積(ベクトル積)、ノルム等を求めることができます。
・行列に関しては、トレースや行列式の計算、また、逆行列、対称行列、エルミート行列、対角行列、上下三角行列などを求めることができます。
####(1)ベクトルの演算
①内積の計算
内積はdot()で計算します。
②外積(ベクトル積)の計算
2つのベクトルをa,bとすると、
a = (a1, a2, a3)
b = (b1, b2, b3)
外積は以下で計算されます。
(a2 * b3 - a3 * b2, a3 * b1 - a1 * b3, a1 * b2 - a2 * b1)
外積はcross()で計算します。
③L1ノルムの計算
求めるベクトルをvとします。
v = (v1, v2, v3)
L1ノルムは、各成分の絶対値の和で求められます。
|v1| + |v2| + |v3|
L1ノルムはnorm(v, 1)で計算します。
(vは求める対象のベクトル)
④L2ノルムの計算
L2ノルムは、各成分の2乗和で求められます。
ユークリッドノルムとも呼びます。
$$
\sqrt{v1^2 + v2^2 + v3^2}
$$
L2ノルムはnorm(v, 2)で計算します。
⑤L∞ノルム(無限大ノルム)の計算
無限大ノルムは、各成分の絶対値の中で最も大きい成分の絶対値をノルムとする方式で、以下のように定義されます。
$$
max_{(i=1,2,...,N)}|v_i|
$$
無限大ノルムはnorm(v, Inf)で計算します。
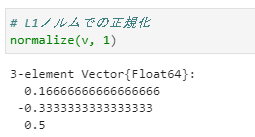
⑥L1ノルムでの正規化
L1ノルムで正規化したベクトルを得るには、normalize(v, 1)を使用します。
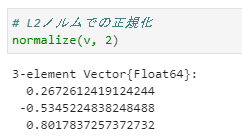
⑦L2ノルムでの正規化
L2ノルムで正規化したベクトルを得るには、normalize(v, 2)を使用します。
####(2)行列の演算
①トレースの計算
求める対象の行列をAとします。
$$
A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 0 & 1 \\ 2 & 5 & 6 \end{pmatrix}
$$
トレースはtr()で計算します。
②行列式の計算
行列式の値はdet()で計算します。
③逆列式の計算
逆行列はinv()で求めることができます。
④対称行列の計算
対称行列はSymmetric()で求めることができます。
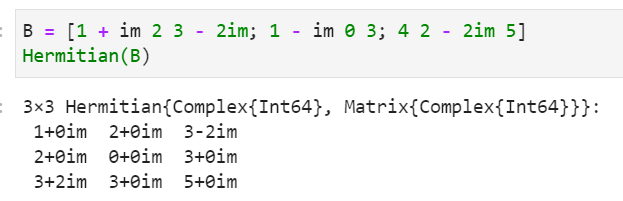
⑤エルミート行列の計算
エルミート行列はHermitian()で求めることができます。
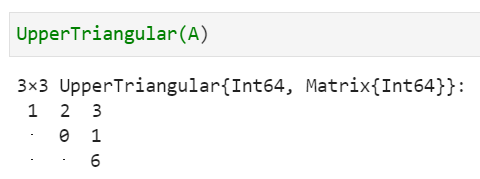
⑥上三角行列の計算
上三角行列はUpperTriangular()で求めることができます。
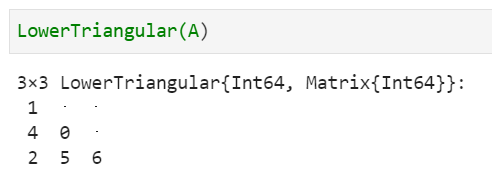
⑦下三角行列の計算
下三角行列はLowerTriangular()で求めることができます。
⑧対角行列の計算
対角行列はDiagonal()で求めることができます。
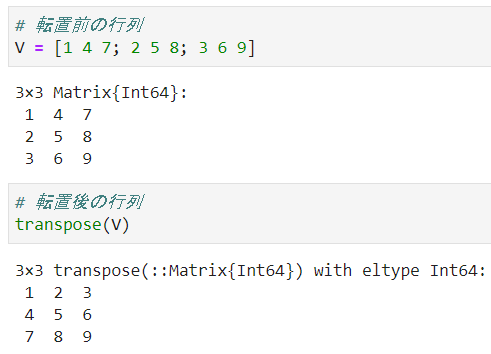
⑨転置行列の取得
transpose()を使用して、行列の転置行列を取得することができます。
この他にも様々な行列計算の関数が用意されています。
詳細は、Juliaの公式ドキュメントを参照して下さい。
##もくじ
Julia早引きノート［01］変数・定数の使い方
Julia早引きノート［02］算術式、演算子
[Julia早引きノート［03］複素数]
(https://qiita.com/ttabata/items/225c77a4d71fafc3e482)
Julia早引きノート［04］正規表現
....
もくじを開く
##関連情報
Julia - 公式ページ
https://julialang.org/
Julia - 日本語公式ドキュメント
https://julia-doc-ja.readthedocs.io/ja/latest/index.html
初めてのJuliaとインストール (Windows & Linux)
https://qiita.com/ttlabo/items/b05bb43d06239f968035
Julia - Mathematics
https://docs.julialang.org/en/v1/base/math/
##ご意見など
ご意見、間違い訂正などございましたらお寄せ下さい。