教師なしの機械学習モデルでもgridsearchCVを使ってパラメータ探索がしたい！

はじめに

機械学習モデルのパラメータ探索で代表的なものにgridsearchがあります．scikit-learnだとGridSearchCVがそれに当たるのですが，これは教師ラベルを持った教師あり学習のモデルにのみ使うことが推奨されています（検証用データを用いて汎化誤差が優れたパラメータを探したいため）．

ただ一方で、教師なし学習でも汎化誤差云々関係なしに単純にパラメータ探したい需要がごく稀によくあると思います（少なくとも自分はそうでした）．自分の場合，勾配法の学習率や次元削減法の次元数を色々変えてみて，ざっくりと目的関数が小さくなる値を見つけたいことがよくありました。

なのでここでは、教師なし学習のモデルでもscikit-learnのgridsearchCVを使ってパラメータを探索するコードを一通り書いてみたので共有したいと思います．また，グリッドサーチした結果がひと目で分かるような可視化のプロットも合わせて紹介したいと思います．

今回使用するコード

全てのコードはここにあります．
https://github.com/tsuno0829/qiita/blob/main/gridsearchCV_for_unsupervised/gridsearchCV_for_unsupervised_ML_model.ipynb

コード

今回使用したライブラリは以下のようになっています

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anim
from mpl_toolkits.mplot3d import Axes3D
from sklearn.base import BaseEstimator
from sklearn.model_selection import GridSearchCV

次に，今回使用した教師なしの機械学習モデルですが，@syusyumk2さんが作成した教師なしカーネル回帰（通称UKR）のコードをお借りしました（一部改変して使っています）．本当にありがとうございます！

UKRの説明については下記の記事が参考になると思います（UKRをとてもざっくりと説明すると非線形なPCA，あるいはGPLVMに似ています．具体的なタスクとして，観測データXに対して，それよりも低次元な潜在変数Zとf:Z→Xとなるような滑らかな非線形写像fの２種類を求めています）．
https://qiita.com/syusyumk2/items/cade1d7d1eb9b5e1108b
https://qiita.com/odiak/items/c64e937d9d5a97530d4e

またここで，GridSearchCVで使用するためにはsklearn準拠モデルにしておく必要があります（ここは教師ありでも同様です）．具体的には，①モデルのクラスにsklearnのBaseEstimatorを継承すること．②classの__ init __にgridsearchで変更したいパラメータを設定できるようにしておくこと③fitを定義しておくこと，の３点が少なくとも必要になります．また③のfitの引数には学習データXを指定できるようにする必要があります．

class UnsupervisedKernelRegression(BaseEstimator):
    def __init__(self, latent_dim=2, learning_rate=0.5, sigma=1.0, lambda_=1e-3):
        self.X = None
        self.X_pred = None
        self.Z = None
        self.n_sample = None
        self.input_dim = None
        self.latent_dim = latent_dim
        self.sigma = 1.0   # カーネルの幅を決定する定数
        self.gamma = 1.0 / (self.sigma **2)
        self.lambda_ = lambda_   # 正則化項の強さを決定する定数
        self.learning_rate = learning_rate   # 勾配法の学習率
        self.history = None   # 学習結果を保存する辞書
    
    def fit(self, X, n_epoch=100):
        self.X = X
        self.n_sample = X.shape[0]
        self.input_dim = X.shape[1]
        self.Z = np.random.normal(loc=0, scale=1e-3, size=(self.n_sample, self.latent_dim))
        self.history = {
            "Z": np.zeros((n_epoch, self.n_sample, self.latent_dim)),
            "X_pred": np.zeros((n_epoch, self.n_sample, self.input_dim))
        }
        
        for epoch in range(n_epoch):
            self.delta = self.Z[:,None,:] - self.Z[None,:,:]
            self.h_kn = np.exp(-1 / (2*self.sigma ** 2) * np.sum((self.Z[None, :, :] - self.Z[:, None, :]) ** 2,axis=2))
            self.g_k = np.sum(self.h_kn,axis=1)
            self.r_ij = self.h_kn/self.g_k[:,None]
            self.X_pred = self.r_ij @ self.X
            self.d_ij = self.X_pred[:, None, :] - self.X[None, :, :]
            self.A = self.gamma * self.r_ij * np.einsum('nd,nid->ni', self.X_pred - self.X, self.d_ij)
            self.bibun = np.sum((self.A + self.A.T)[:, :, None] * self.delta, axis=1)
            self.Z -= self.learning_rate * (self.bibun + self.lambda_*self.Z)
            # 学習結果を保存する
            self.history["Z"][epoch] = self.Z
            self.history["X_pred"][epoch] = self.X_pred
    
    def reconstruction_loss(self, X_true, X_pred):
        N = X_true.shape[0]
        dist = X_pred - X_true
        loss = 0.5 * np.sum(dist ** 2) / N
        return loss

モデルを定義した後は，学習データとモデルのインスタンスを作ります．
学習データはn_sample個でノイズも含めて１０次元の人工データ（サドルシェイプデータ）を使用しました．

n_sample = 200   # データ数
n_epoch=500   # 学習回数

# 学習データは，3次元のサドルシェイプデータを使用する
# 加えて，１０次元のノイズは加えておく
X = np.random.normal(loc=0, scale=0.1, size=(n_sample, 10))
data = np.random.rand(n_sample, 2) * 2 - 1
X[:, 0] += data[:, 0]
X[:, 1] += data[:, 1]
X[:, 2] += data[:, 0] ** 2 - data[:, 1] ** 2

# 今回テストで使用する教師なしの機械学習モデル（通称UKR）
# 観測データXに対応する低次元の潜在変数Zと非線形な滑らかな写像f: Z→Xの２種類を学習する
# 大雑把にいうと，　非線形のPCAやGPLVM
model = UnsupervisedKernelRegression()

ここからGridSearchCVを使って教師なしモデルを学習する部分になります．
まず，モデルの__ init __で変更したいパラメータを指定します．今回は潜在空間の次元数と勾配法の学習率をいろいろ変えてみます．

# 今回変えるパラメータを辞書で登録する
# このパラメータは各自が用意したモデルの__init__の引数によって変える
# パラメータはスカラー値のものしか指定できないことに注意
params = {
    'latent_dim':  [1, 2, 3],   # 潜在空間の次元数
    'learning_rate': [1000, 100, 10, 1, 0.1],   # 勾配法の学習率
}

次に，スコア関数を定義します（教師ありの場合はここが汎化誤差にあたる部分）．今回はUKRの学習で使う目的関数（いわゆるデータとその推定点の二乗誤差）を関数として用意しました．返り値はスカラーにしておく必要があるので注意です．

# gridsearchでパラメータの良し悪しを判断するための評価関数
# 返り値はスカラーのスコア値にする
# ここでは，単純にUKRの目的関数（学習データの復元誤差）を評価関数に使用する
def scorer(model, X):
    score = model.reconstruction_loss(
        X_true=X,
        X_pred=model.X_pred
    )
    return score

このGridSearchCVの部分が肝になります．といっても使用するときはこのままコピペしてしまってもいいと思います．先程用意したparamsとscorerをそれぞれ設定し，cv（cross validationのこと）をcv=[(slice(None), slice(None))]として使用しないことを明記するだけです．あとはそのままgs.fitで学習してしまうだけです．

# GridSearchCVの設定
# 教師なしのため，　CrossValidationは全くしないことに注意
gs = GridSearchCV(
    estimator=model,
    param_grid=params,
    scoring=scorer,
    cv=[(slice(None), slice(None))],
    verbose=1,
    n_jobs=3,
)

# グリッドサーチを実行する
# 教師なしなので， yはNoneを指定する
# UKR.fitの引数もここで指定できる一方で，　Xとyは必ず指定しないといけないことに注意する
gs.fit(X=X, y=None, n_epoch=n_epoch)

# パラメータとそのパラメータで学習したときのスコア値を表示する
for param, score in zip(gs.cv_results_['params'], gs.cv_results_['mean_test_score']):
    print(f'score:{score:.3f} param: {param}')

# 学習結果はこんな感じになります．
# 全てのパラメータの組み合わせとそれに対するスコア関数の値がそれぞれ得られている事がわかります．
>Fitting 1 folds for each of 15 candidates, totalling 15 fits
>[Parallel(n_jobs=3)]: Using backend LokyBackend with 3 concurrent workers.
>[Parallel(n_jobs=3)]: Done  15 out of  15 | elapsed:   11.7s finished
>score:0.201 param: {'latent_dim': 1, 'learning_rate': 1000}
>score:0.266 param: {'latent_dim': 1, 'learning_rate': 100}
>score:0.084 param: {'latent_dim': 1, 'learning_rate': 10}
>score:0.076 param: {'latent_dim': 1, 'learning_rate': 1}
>score:0.134 param: {'latent_dim': 1, 'learning_rate': 0.1}
>score:0.240 param: {'latent_dim': 2, 'learning_rate': 1000}
>score:0.020 param: {'latent_dim': 2, 'learning_rate': 100}
>score:0.023 param: {'latent_dim': 2, 'learning_rate': 10}
>score:0.028 param: {'latent_dim': 2, 'learning_rate': 1}
>score:0.051 param: {'latent_dim': 2, 'learning_rate': 0.1}
>score:0.354 param: {'latent_dim': 3, 'learning_rate': 1000}
>score:0.010 param: {'latent_dim': 3, 'learning_rate': 100}
>score:0.006 param: {'latent_dim': 3, 'learning_rate': 10}
>score:0.009 param: {'latent_dim': 3, 'learning_rate': 1}
>score:0.050 param: {'latent_dim': 3, 'learning_rate': 0.1}

ただこのままスコアを表示しても味気ないし，パラメータの組み合わせが多いときに直感的では全然ないと思いますのでこれらを可視化します．
具体的には平行座標という可視化方法があってこのグリッドサーチと相性が良かったので作ってみました．matplotlibで平行座標を作る方法を見つけられなかったので今回はplotlyを使用しました．

# 平行座標表示でパラメータとスコアを可視化する
import pandas as pd
df = pd.DataFrame(gs.cv_results_['params'])
df['loss'] = gs.cv_results_['mean_test_score']

import plotly.graph_objects as go
from sklearn import preprocessing

le = preprocessing.LabelEncoder()
et = list(df['learning_rate'])
le.fit(et)
et_le = le.transform(et)

fig = go.Figure(
    data=go.Parcoords(
        line=dict(color=df['loss'],
                  colorscale='Bluered_r',
                  showscale=True),
        dimensions=list([
            dict(label='latent_dim',
                values=df['latent_dim']),
            dict(tickvals=le.transform(np.sort(list(set(df['learning_rate'])))),
                ticktext=np.sort(list(set(df['learning_rate']))),
                label="learning_rate",
                values=et_le),
            dict(range=[0, max(df['loss'])],
                label='ukr_loss',
                values=df['loss'])
        ])
    )
)
fig.show()

可視化してみると以下のgifです．
左列が潜在空間の次元（１〜３）で真ん中の列が勾配法の学習率，右列がスコア（今回はUKRの目的関数）になっています．
スコアの良い悪いが一目瞭然で分かることや，次元が２や３みたいな要領で絞り込みつつもスコアが良いパラメータといった感じでパラメータを絞り込むことがインタラクティブにできることが特徴です．

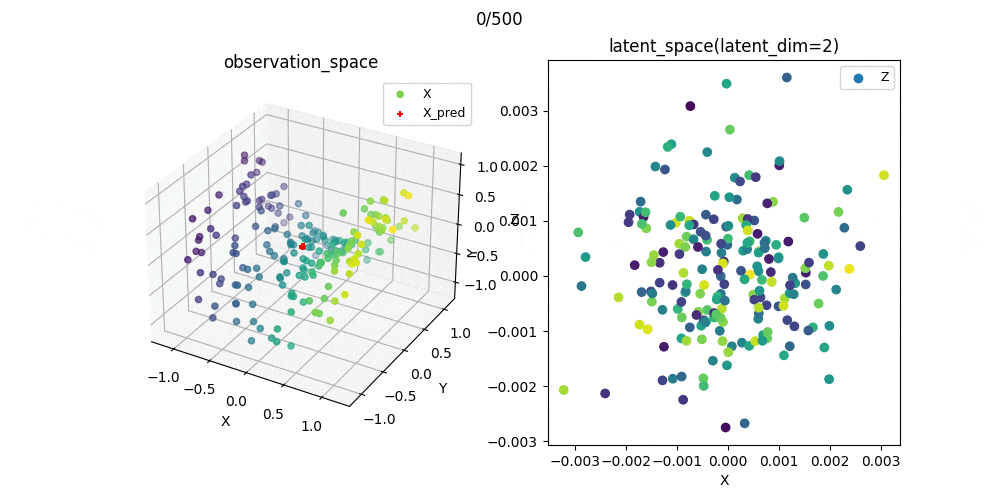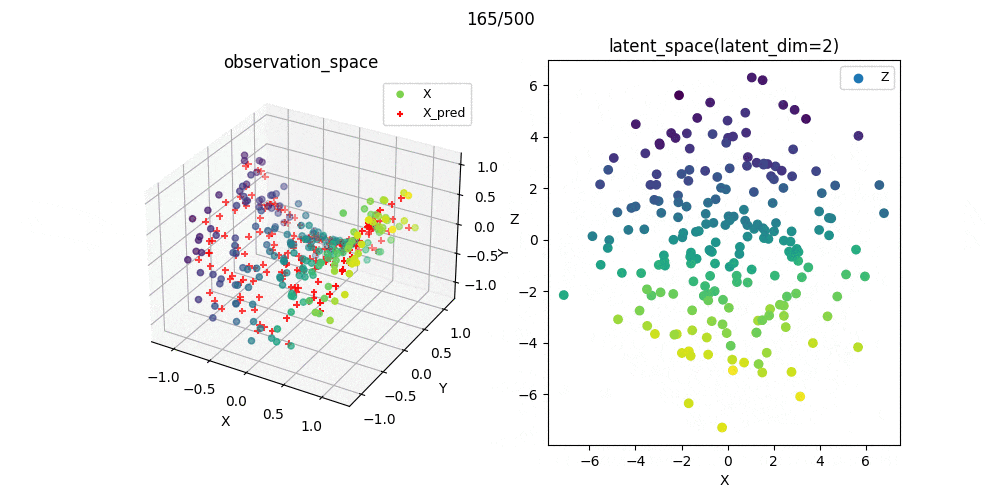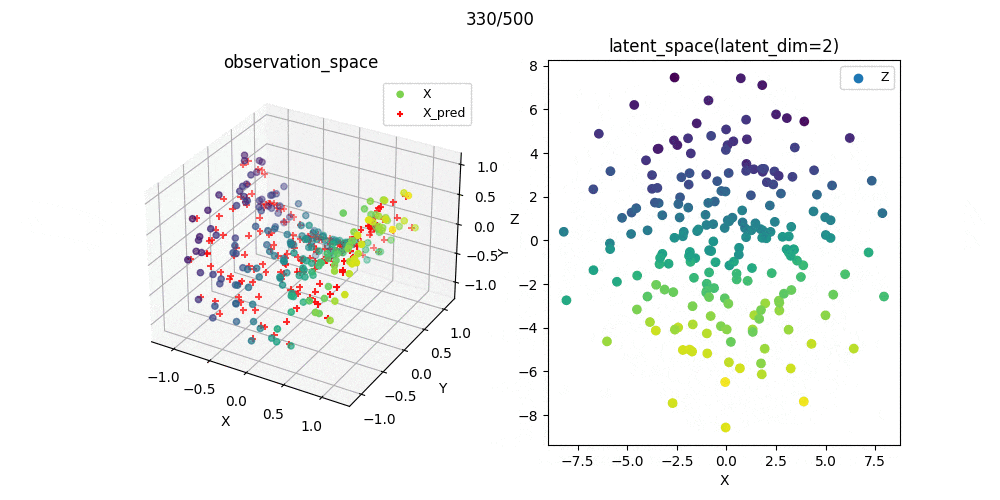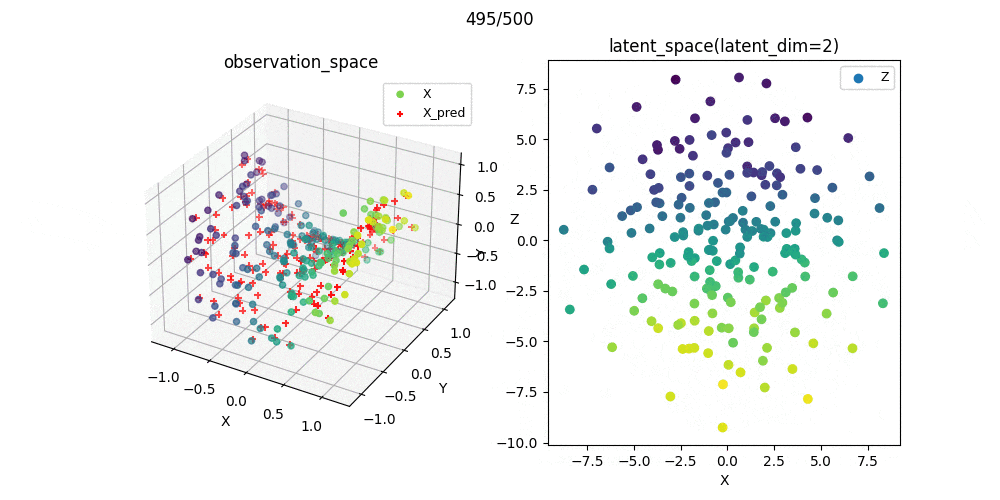
また，この可視化結果を参考にパラメータを選んで学習過程をプロットしたときのgifがこれです．
教師なし学習なので，必ずしもスコアが小さいから汎化性能がある（もしくは学習が上手くいっている）わけではありませんが，ここでは問題なく学習できたパラメ➖タを選択できたことが分かりました．

%matplotlib nbagg
# gridsearchでlossが低かったパラメータを選んで実際に学習結果を可視化してみる
model = UnsupervisedKernelRegression(latent_dim=2, learning_rate=1)
model.fit(X=X, n_epoch=n_epoch)

# 描画
n_skip = 5
fig = plt.figure(1,figsize=(10, 5))
ax1 = fig.add_subplot(121,projection='3d')
ax2 = fig.add_subplot(122)
X_pred = model.history["X_pred"][::n_skip]
Z = model.history["Z"][::n_skip]

def update(i):
    ax1.cla()
    ax2.cla()
    ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=X[:, 0], label='X')
    ax1.scatter(X_pred[i, :, 0], X_pred[i, :, 1], X_pred[i, :, 2], color='red', s=25, marker='+', label='X_pred')
    ax2.scatter(Z[i, :, 0], Z[i, :, 1], c=X[:, 0], label='Z')
    ax1.set_title('observation_space', fontsize=12)
    ax1.set_xlabel("X")
    ax1.set_ylabel("Y")
    ax1.set_zlabel("Z")
    ax2.set_title('latent_space(latent_dim=2)', fontsize=12)
    ax2.set_xlabel("X")
    ax2.set_ylabel("Y")
    ax1.legend(fontsize=9)
    ax2.legend(fontsize=9)
    plt.suptitle(f'{i*n_skip}/{n_epoch}')
ani = anim.FuncAnimation(fig, update, interval=200, frames=n_epoch//n_skip)
ani.save('saddle_shape.gif', writer='imagemagick')
# plt.show()

最後に

頻繁に使うわけではないですが，たまに欲しくなるのと，ネットにここらへんの情報がなかったので練習がてら自分で作ってみました．
素人が作ったものなので，間違っている点や更に良い方法がありましたら教えて頂けると幸いです．