Juliaに入門して教師なしカーネル回帰を実装してみる

ご存知の方も多いと思いますが、Juliaというプログラミング言語があります。
この言語では、配列の配列ではない多次元配列が言語レベルでサポートされているなど、科学計算に有用な機能や標準ライブラリが多く含まれています。他にも、配列のインデックスが1始まりだったり、動的型付けの言語でありながら関数のアノテーションをサポートしていて多重ディスパッチが使えたり、JITコンパイラのおかげで高速な計算ができたりといった特徴もあります。

僕は以前よりこの言語に興味があり、ドキュメントを読んだり少し書いてみたりはしていたのですが、まだあまり入り込めていませんでした。というのも、パッケージ管理の仕組みがわかりにくかったり、いくつかの外部パッケージがPythonに依存していてビルドに失敗することがあったり、などのつまづきポイントがあったからです。

最近、Juliaクックブックという本が出版されました。もちろん買いました。良い機会なので、Juliaに再び入門してみることにしました。

急いで書いたので、超てきとうです。おかしなところがあればご指摘ください。
また、機械学習を題材にしていますが、あくまでJuliaを触ってみることが主な目的であり、多少正確さに欠くところがあるかもしれません。

Juliaのインストール

詳細はPlatform specific instructionsを見てください。
Windowsならexeのインストーラー、macOSならインストーラーまたはhomebrewから、Linuxはダウンロードしたファイルを解凍して/usr/localに置くだけです。

Juliaの文法について

前述のクックブックまたは公式ドキュメントを読んでください。

その中でも、僕が気に入ったポイントをいくつか書いてみます。

• 多次元配列のサポート
  • 多次元配列は演算子や関数のブロードキャストをサポートしていて、スカラー値を扱う演算子や関数に . をつけるだけでブロードキャストされる
• ベースは動的型付けでありながら、型アノテーションをサポートしている
  • その恩恵もあり、関数のオーバーロード(多重ディスパッチ)が可能
• マクロ

教師なしカーネル回帰(unsupervised kernel regression; UKR)について

詳細は論文をご参照ください。

簡単に言うと、データを低次元空間に埋め込み、低次元空間からデータ空間へのなめらかな写像を推定する教師なし学習の一手法です。

D次元のデータセット $\mathrm{Y} \in \mathbb{R}^{N \times D} $ から、 L次元の潜在変数 $ \mathrm{X} \in \mathbb{R}^{N\times L}$ を得ます。
そのとき、潜在空間からD次元空間への写像 $f$ は、次のように表されます。

f(\mathbf{x}^*; \, \mathrm{X},\, \mathrm{Y}) = \sum_{n=1}^{N} \mathbf{y}_{n} \frac{\mathrm{K}(\mathbf{x}_n, \, \mathbf{x}^*)}
{\sum_{n'=1}^{N} \mathrm{K}(\mathbf{x}_{n'}, \, \mathbf{x}^*)}

Kはカーネル関数です。今回はガウスカーネル $ \mathrm{K}(\mathbf{x},, \mathbf{x}') = \mathrm{exp}\left(-\frac{1}{2}\left\|\mathbf{x}-\mathbf{x}'\right\|^2\right) $ を使いましょう。

次に、目的関数を定義します。すべてのデータの潜在変数が、もとのデータに近い値に写像されるようにします。

\mathrm{E}(\mathrm{X}; \, \mathrm{Y}) = \frac{1}{\mathrm{N}} \sum_{n=1}^N \| \mathbf{y}_n - f(\mathbf{x}_n;\, \mathrm{X},\, \mathrm{Y}) \|^2

Eを最小化するようにXを求めます。実際には、Xの分散を大きくすることでEをいくらでも小さくできてしまうため、Xの正則化項を導入したほうが良いのですが、ここでは省略します。
これをJuliaで実装していきましょう。

JuliaでUKRを実装する

まず、いくつか必要なパッケージをインストールします。プロジェクトのディレクトリに移動して、juliaコマンドを実行してREPLに入ります。

$ julia
               _
   _       _ _(_)_     |  Documentation: https://docs.julialang.org
  (_)     | (_) (_)    |
   _ _   _| |_  __ _   |  Type "?" for help, "]?" for Pkg help.
  | | | | | | |/ _` |  |
  | | |_| | | | (_| |  |  Version 1.2.0 (2019-08-20)
 _/ |\__'_|_|_|\__'_|  |  Official https://julialang.org/ release
|__/                   |

julia>

次に、]キーを押すと、REPLがパッケージ管理モードになります。そこで、次のようにします。

(v1.2) pkg> activate .
Activating new environment at `~/my-project/Project.toml`

(my-project) pkg> add PyPlot
...
(my-project) pkg> add ForwardDiff
...

最初のactivateでプロジェクトの設定を読み込み、なければ設定ファイルを作成します。
その次に、addコマンドでパッケージをインストールしています。今回は、プロットのためのPyPlotと自動微分のためにForwardDiffパッケージを使用します。

---

さて、必要なものが揃ったのでコードを書いていきましょう。

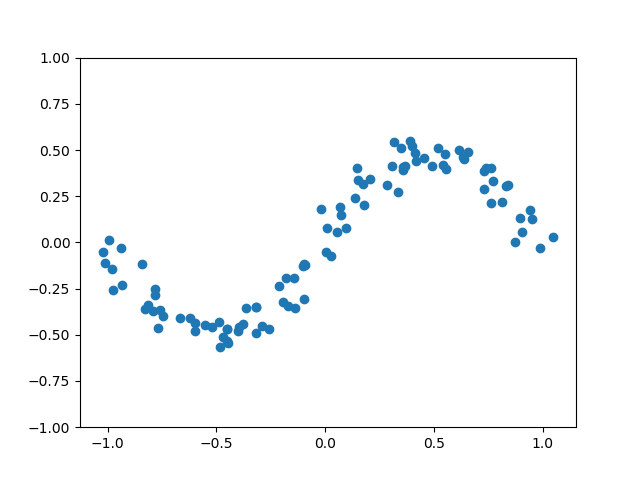
まず、学習するためのデータを生成して表示してみます。

main.jl

using Random, PyPlot

function main()
    Random.seed!(13)

    N = 100
    D = 2
    t = range(-1, 1, length = N)
    Y = zeros(N, D)
    Y[:, 1] = t
    Y[:, 2] = sin.(π * t) * 0.5
    Y += randn(size(Y)) * 0.05

    ylim(-1, 1)
    scatter(Y[:, 1], Y[:, 2])
    show()
end

main()

• sin関数を使って生成した100個の2次元空間の点に、ノイズを加えています。
• main関数を定義してすぐ実行していますが、名前はmainでなくて良いです。また、Juliaではあまりトップレベルにコードを書かないほうが良いらしく、関数をわざわざ作っているのもそのためです。
• インデックスが1始まりですね！
• sin.() というふうに呼び出していますが、これがブロードキャストです。
• π のようなユニコード文字も名前に使えます。ちなみに π は組み込みの定数です。
  • 他にも、非アスキー記号が演算子に使えたりもしたはず。組み込みだと√とか。

そんなことはさておき、実行してみましょう。

$ julia --project=. main.jl

すると、こんな絵が表示されます。じゃーん！

次に、写像fを表現する関数を実装してみます。

function f(X, Y, X_in)
    C = dropdims(
        sum(
            (
                reshape(X_in, size(X_in, 1), 1, size(X_in, 2)) .-
                reshape(X, 1, size(X, 1), size(X, 2))
            ) .^ 2,
            dims = 3,
        ),
        dims = 3,
    )
    K = exp.(-0.5C)
    K_ = K ./ sum(K, dims = 2)
    K_ * Y
end

• 演算子のブロードキャストも出てきました。演算子の前に.をつけるだけです。
• 0.5Cという記述が見えますが、これは、0.5 * Cと同じです。
• 関数の最後の行は、返り値を表す式です。Juliaでは明示的にreturnを書く必要がありません。
• 返り値の式は、行列積です。

続いて、データYからXを推定する関数を実装します。

using Random, PyPlot, ForwardDiff

function estimate(Y::Array{Float64,2}, Q::Int)::Array{Float64,2}
    N = size(Y, 1)
    X = randn(N, Q) * 0.05

    loss = X -> sum((Y - f(X, Y, X)) .^ 2) / N

    println(loss(X))
    for i in 1:100
        X .-= 60.0 * ForwardDiff.gradient(loss, X)
        println(loss(X))
    end

    X
end

• 今度は、関数に型アノテーションを書いてみました。
• FowardDiffパッケージを使って、損失関数の勾配を計算し、それを定数倍してXから引いています。
• とりあえず100回更新してみます。

最後に、これらを組み合わせます。

main.jl

using PyPlot, ForwardDiff, Random

function f(X, Y, X_in)
    C = dropdims(
        sum(
            (
                reshape(X_in, size(X_in, 1), 1, size(X_in, 2)) .-
                reshape(X, 1, size(X, 1), size(X, 2))
            ) .^ 2,
            dims = 3,
        ),
        dims = 3,
    )
    K = exp.(-0.5C)
    K_ = K ./ sum(K, dims = 2)
    K_ * Y
end

function estimate(Y::Array{Float64,2}, Q::Int)::Array{Float64,2}
    N = size(Y, 1)
    X = randn(N, Q) * 0.05

    loss = X -> sum((Y - f(X, Y, X)) .^ 2) / N

    println(loss(X))
    for i in 1:100
        X .-= 60.0 * ForwardDiff.gradient(loss, X)
        println(loss(X))
    end

    X
end

function main()
    Random.seed!(13)

    N = 100
    t = range(-1, 1, length = N)
    Y = zeros(N, 2)
    Y[:, 1] = t
    Y[:, 2] = sin.(π * t) * 0.5
    Y += randn(size(Y)) * 0.05

    X = estimate(Y, 1)

    Y_estimated = f(X, Y, X)
    scatter(Y[:, 1], Y[:, 2])
    plot(Y_estimated[:, 1], Y_estimated[:, 2], c = "r")
    ylim(-1, 1)
    show()
end

main()

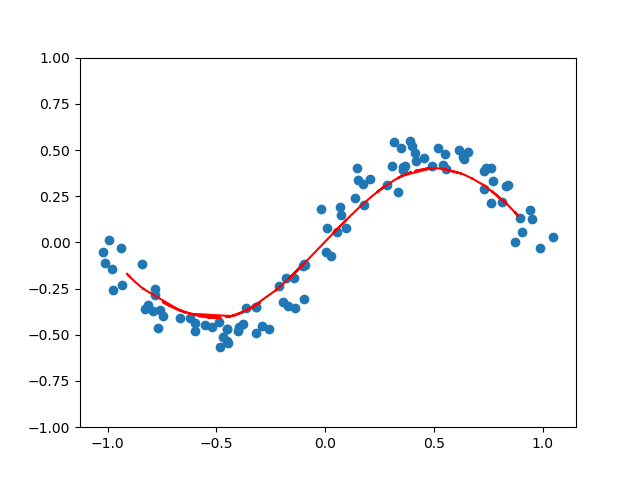
さあ、実行してみましょう。printlnでloss関数の値を出力しているので、だんだん学習がするんでいく様子がわかります。そしてどーん！

無事に絵が表示されました。やったー！
推定したXの値は表示していませんが、潜在変数と、潜在変数からデータ空間へのなめらかな写像が推定できたようです。(きっと)

雑な駆け足ではありましたが、これで無事にJuliaに再入門できました。めでたし。

おわりに

最近は機械学習やデータ分析などに、Pythonが使われることが増えていると思います。僕も仕事で使っています。
ところが、Pythonは実行がどちらかと言うと遅いほうですし、文法もイマイチだなと感じることもしばしばあります。(Numpyを中心としたライブラリたちがすごいのでそれでも使われているのですが...)

そんなPythonに不満を感じていた頃、Juliaという言語を知り、ドキュメントなどを読んでいて、これは面白い言語だなぁと思っていました。その後しばらく放置していましたが、Juliaクックブックとアドベントカレンダーがきっかけになりこうしてまた触る機会ができました。今後ももう少し使っていきたいと思います。

この投稿をきっかけにして、Juliaを始めてみる人が1人でも増えると嬉しいです。

あと、Juliaに興味がある方はTwitterで黒木玄さん@genkurokiや、@bicycle1885さんあたりをフォローすると良いかもしれません。
それでは良いJuliaライフを〜