この記事は古川研究室 Advent_calendar 1日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
はじめに
本記事では自分が実際に組んでみたUKR(Unsupervised Kernel Regression)なるものについて紹介しようと思います。和訳すると教師なしカーネル回帰ですね、この論文を読んで実装しました。
多様体学習などに興味のある方は是非組んでみて下さい。
UKRのやりたいこと
UKRがやりたいことは観測データ$\mathbf{Y}=(\mathbf{y}_1,\mathbf{y}_2,...\mathbf{y}_N)\in \mathbb{R}^{D×N}$と各観測データに対応した潜在変数
$\mathbf{X}=(\mathbf{x}_1,\mathbf{x}_2,...\mathbf{x}_N)\in \mathbb{R}^{M×N}$を繋ぐ滑らかな写像$\mathbf{f}:\mathbb{R}^{M}→\mathbb{R}^{D}$を推定することです。
写像$\mathbf{f}$は以下の式で推定します。
\mathbf{f}(\mathbf{x} ; \mathbf{X})=\sum_{i} \mathbf{y}_{i} \frac{K\left(\mathbf{x}-\mathbf{x}_{i}\right)}{\sum_{j} K\left(\mathbf{x}-\mathbf{x}_{j}\right)}\tag{1}
見覚えのある方もいるのではないでしょうか。この式はNadaraya-Watoson推定とほぼ同じ式です。
見慣れない方のために説明すると式中の$K$はカーネル関数と呼ばれ、本記事では以下の式で定義します。
K\left(\mathbf{x}-\mathbf{x}^{\prime}\right)=\exp \left(\frac{-1}{2h}\left\|\mathbf{x}-\mathbf{x}^{\prime}\right\|^{2}\right)
またこのカーネル関数はガウスカーネルとも呼ばれます。
Nadaraya-Watosonとの違いはカーネル幅$h$が論文では$1$に固定されているというところだけですね
※Nadaraya-Watoson推定についてはこの記事で詳しく説明してくれています。
(1)式で潜在変数を観測空間へ写像し、以下の式で観測データとの誤差を計算します。
R(\mathbf{X})=\frac{1}{N} \sum_{i}\left\|\mathbf{y}_{i}-\mathbf{f}\left(\mathbf{x}_{i} ; \mathbf{X}\right)\right\|^{2}\tag{2}
勾配法によってこの誤差を小さくしていき、潜在変数を更新していきます。
実装する際には自動微分を使うか、自らで実際に微分を行ってその式をプログラムで書き記すしかありません。本記事では頑張って己で微分した式を用いています。式展開を全て書くとかなり長くなり僕への負担もすごいので最終結果のみ載せます。
※式の簡単化のため、以下の変数を定義しています。
r_{ij}=\frac{K\left(\mathbf{x}_{i}-\mathbf{x}_{j}\right)}{\sum_{j^{\prime}} K\left(\mathbf{x}_{i}-\mathbf{x}_{j^{\prime}}\right)}
\mathbf{d}_{ij}=\mathbf{f}(\mathbf{x}_{j};\mathbf{X})-\mathbf{y}_{i}
\mathbf{\delta}_{ij}=\mathbf{x}_{i}-\mathbf{x}_{j}
これらの変数を用いると、(2)式の微分は以下のように表されます。
※この微分は論文から引用したものではありません。論文のものと一致するかは確認していないのでご注意ください
\frac{1}{N} \frac{\partial}{\partial \mathbf{x}_{n}} \sum_{i}\left\|\mathbf{y}_{i}-\mathbf{f}(\mathbf{x}_{i};\mathbf{X})\right\|^{2}=\frac{2}{N}\sum_{i}\left[r_{n i} \mathbf{d}_{n n}^{\mathrm{T}} \mathbf{d}_{n i} \boldsymbol{\delta}_{n i}-r_{i n} \mathbf{d}_{i i}^{\mathrm{T}} \mathbf{d}_{i n} \boldsymbol{\delta}_{i n}\right]
全体の流れとしては
(1)式で写像を推定
(2)式で誤差が最小となるように勾配法で潜在変数の更新を繰り返す
となります。
実装結果
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import*
import matplotlib.animation as anm
fig = plt.figure(1,figsize=(14, 6))
ax1 = fig.add_subplot(121,projection='3d')
ax2 = fig.add_subplot(122)
class UKR:
def __init__(self,N,w,z,D,L):
self.N = N
self.zeta = z
self.x = w
self.f = []
self.hist =[]
self.sigma = 1.0
self.lamda = 0.1
self.test = []
self.lr = 1.0
self.D = D
self.L = L
self.gamma = 1.0 / (self.sigma * self.sigma)
def fit(self,T):
self.history = {"z":np.zeros((T, self.N, self.L)),
"Y":np.zeros((T, self.N ,self.D))}
for t in range(T):
self.delta = self.zeta[:,None,:] - self.zeta[None,:,:]
self.h_kn = np.exp(-1 / (2*self.sigma ** 2) * np.sum((self.zeta[None, :, :] - self.zeta[:, None, :]) ** 2,axis=2))
self.g_k = np.sum(self.h_kn,axis=1)
self.r_ij = self.h_kn/self.g_k[:,None]
self.f = np.zeros((self.N,self.D))
self.f = self.r_ij @ self.x
self.d_ij = self.f[:,None,:] - self.x[None,:,:]
self.A = self.gamma * self.r_ij * np.einsum('nd,nid->ni', self.f - self.x, self.d_ij)
self.bibun = np.sum((self.A + self.A.T)[:, :, None] * self.delta, axis=1)
self.zeta -= self.lr*(self.bibun + self.lamda*self.zeta)
self.history["Y"][t] = self.f
self.history["z"][t] = self.zeta
if __name__=="__main__":
N=20#データ数
T=50
w = np.zeros((N*N,3))
latent_space=np.random.normal
zeta = np.dstack(np.meshgrid(np.linspace(-1,1,N),np.linspace(-1,1,N),indexing='ij'))
zeta = np.reshape(zeta,(N*N,2))
for i in range (N*N):
mesh = zeta[i,0]**2-zeta[i,1]**2
w[i] = np.append(zeta[i],mesh)
np.random.seed(1)
i=0
ukr = UKR(N*N,w,zeta,3,2)
ukr.fit(T)
kekka = ukr.history["Y"]
kekka = np.reshape(kekka,(T,N,N,3))
k = ukr.history["z"]
k = np.array(k)
def update(i, zeta,w):
print(i)
ax1.cla()
ax2.cla()
ax1.scatter(w[:, 0], w[:, 1], w[:, 2], c=w[:, 0])
ax1.plot_wireframe(kekka[i,:,:,0],kekka[i,:,:,1],kekka[i,:,:,2])
ax2.scatter(k[i,:,0],k[i,:,1],c=w[:,0])
ax1.set_xlabel("X_axis")
ax1.set_ylabel("Y_axis")
ax1.set_zlabel("Z_axis")
ax2.set_title('latentspace')
ax2.set_xlabel("X_axis")
ax2.set_ylabel("Y_axis")
ani = anm.FuncAnimation(fig, update, fargs = (zeta,w), interval = 500, frames = T-1)
ani.save("test.gif", writer = 'imagemagick')
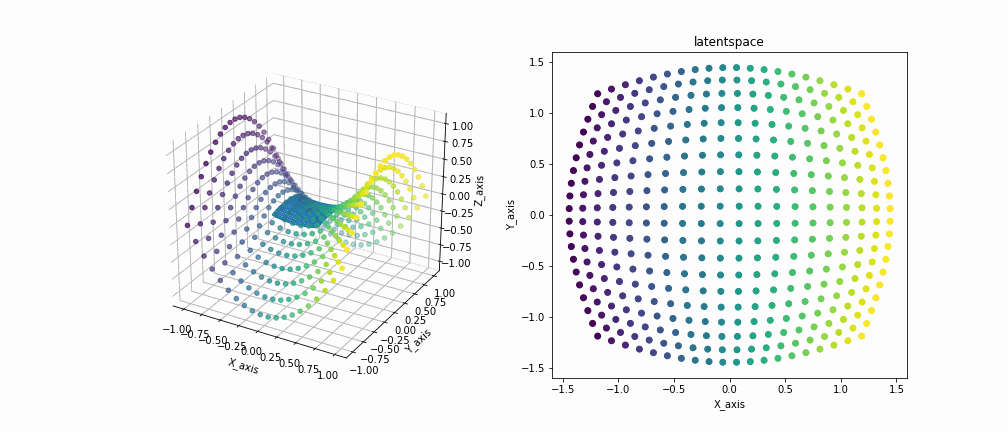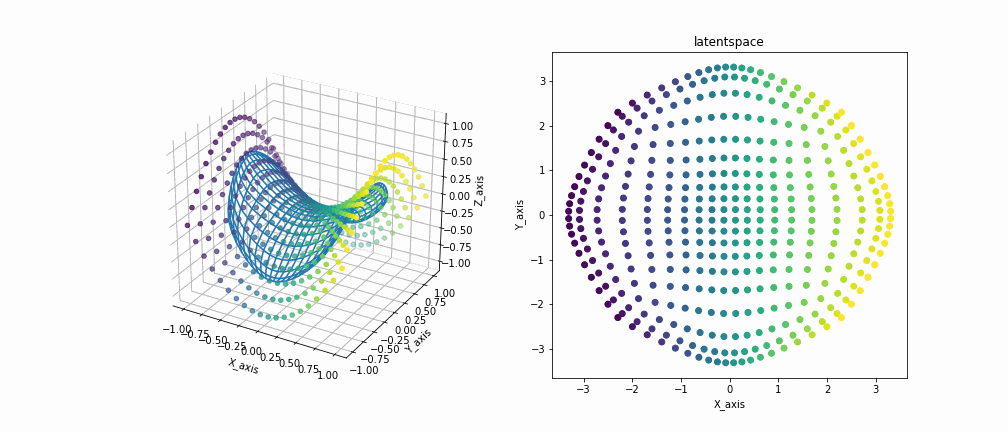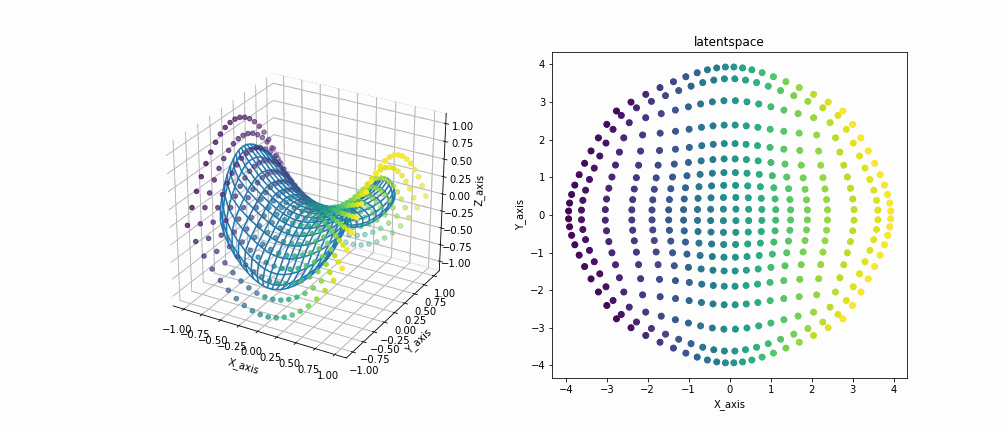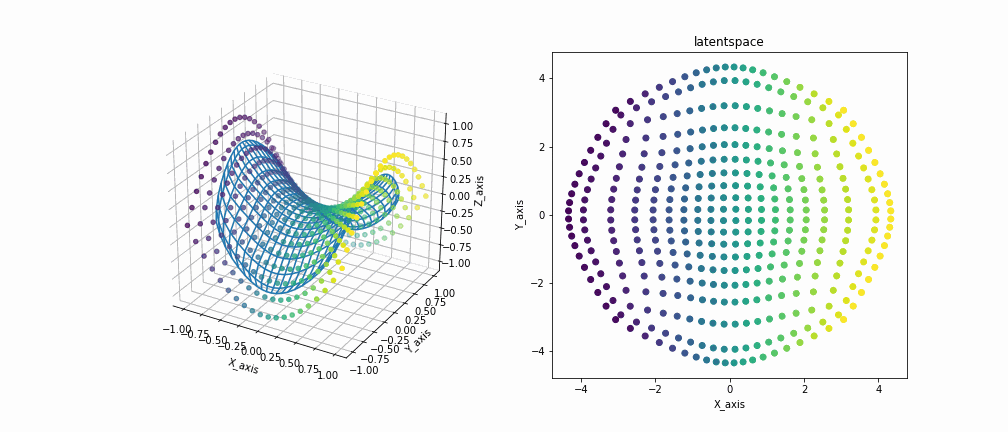
鞍型データを観測データとして与えた場合の実装結果です。
左の図が観測空間を示しており、各点が観測データ、メッシュが写像されたデータをつないだ多様体を示しています。右の図は潜在空間を示しています。
多様体が徐々にじわじわと観測データを覆い尽くしていくのがいいですね 見ててなかなか飽きないです。
参考文献
Variants of unsupervised kernel regression: General cost functions