この記事は古川研究室 Workout calendar 7日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.
一回ほとんど書いてた記事が全部消えて夜中に吠えました. 「下書き保存」と友達になりましょう.
前回のおさらい
前回の記事 Nadaraya-Watson推定 と k近傍法(前編)では 回帰の問題設定を述べ, その回帰を解く手法の一つとしてk近傍法を解説しました。
回帰の問題設定
given: $D$次元ベクトルの観測データ$\mathbf{x} \in \mathbb R^D$とラベル$y \in \mathbb R$のペア$\left\{ ( \mathbf{x}_n,y_n )\right\} _{n=1}^N $
estimate: $y \simeq f(\mathbf{x})$となるような写像 $f$
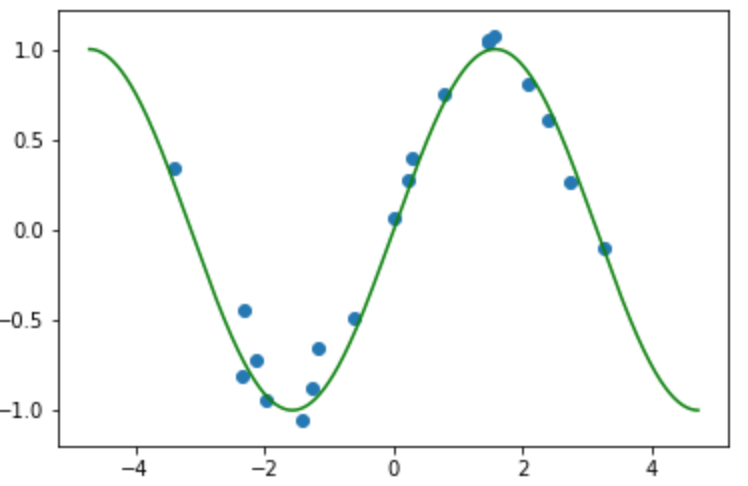
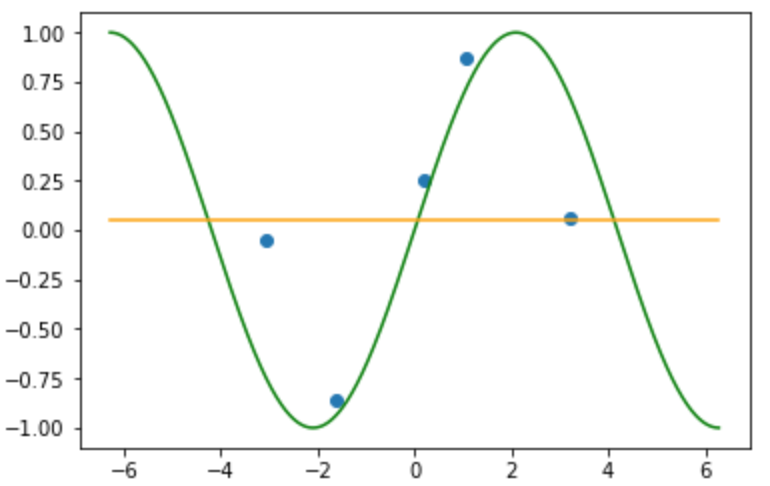
横軸はデータ$x$軸, 縦軸はラベル$y$軸の図です. 真の関数(緑線)にノイズが加わって, 入力(青点)を得ます. 真の関数がわからない中でデータとラベル集合を使って写像を推定してします.
k近傍法
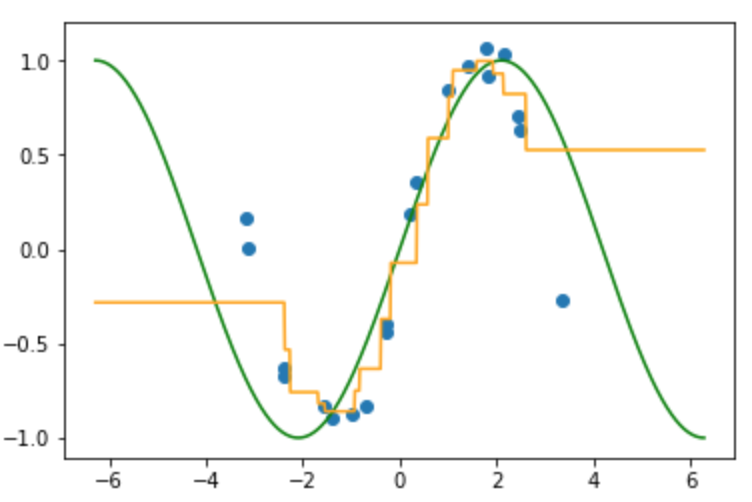
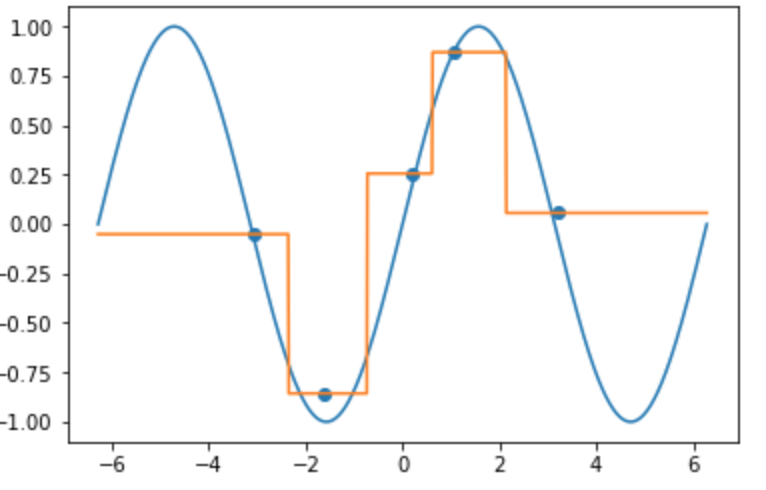
真の関数(緑線)にノイズが加わった入力(青点)が得られている状況で, 4つの近傍のラベルの平均として得られた写像 $f$ (オレンジ線)が以下の図になります.
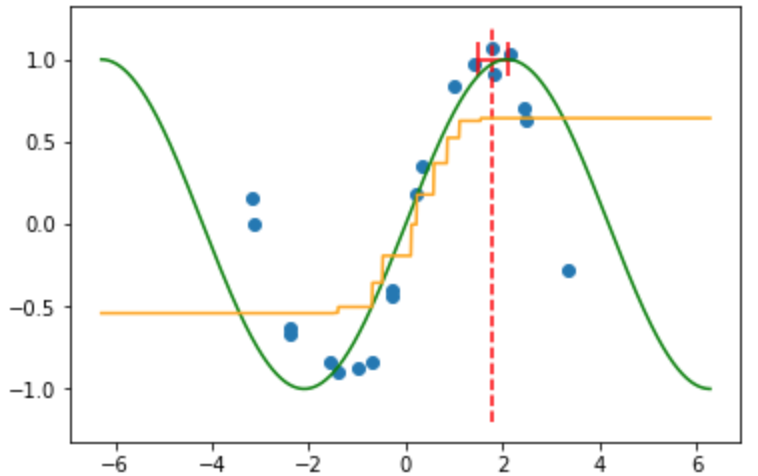
着目点(赤点線: $x=1.8$)とそこの近傍の範囲(赤線)
k近傍法は重みや基底関数を使わずに写像を推定していますが, その推定した写像は不連続な写像になっており微分ができません.
Nadaraya-Watson推定
Nadaraya-Watson推定(NW)は回帰手法の一つです.
k近傍では近傍に含むデータに等しい重みを付与して(平均)していますが, Nadaraya-Watson推定では着目点とデータの距離に応じて滑らかに減少する重みを与えます.
Nadaraya-Watson重み付きカーネル平均はカーネル関数を使って以下の式で与えられます.
f(\mathbf{x}) = \frac{\sum_{i=1}^N K_\lambda(\mathbf{x},\mathbf{x}_i)y_i}{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}
今回 カーネル関数$K_\lambda(\mathbf{x},\mathbf{x_j})$は次式で与えます.
K_\lambda(\mathbf{x},\mathbf{x_j}) = \exp(\frac{-1}{2\sigma^2}||\mathbf{x} - \mathbf{x_j}||^2)
この式はガウス関数の式と等価です. 他のカーネル関数としてはイパネクニコフ関数や短形3次関数が一般的です.
「カーネル関数, 」と続けますと本一冊書くのにちょうどいい分量になるので省略し, ここではカーネル関数 $K_\lambda(\mathbf{a},\mathbf{b})$は$\mathbf{a}=\mathbf{b}$のとき最大値の1をとること, $\mathbf{a}$ と$\mathbf{b}$の近さを表す値になっているということだけを押さえましょう.
実装
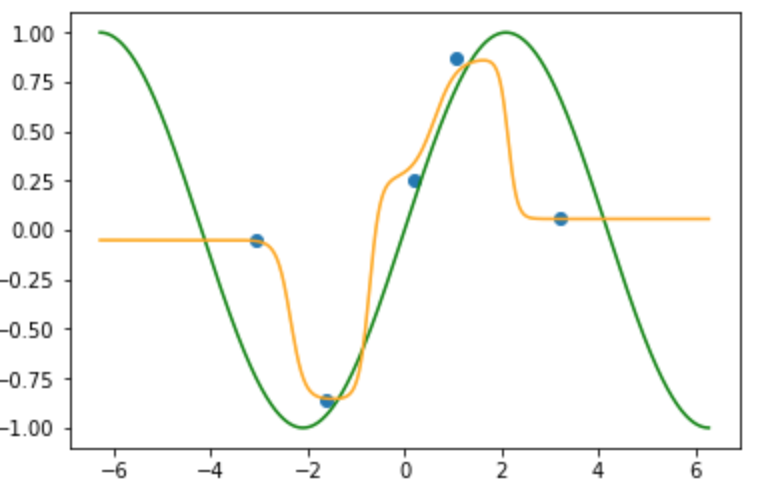
k近傍法と同様の状況です.(データ数は5)
近傍半径: 0.2のとき
def NW(sigma=0.2):
global H, R, Y
Delta = x[:,None] - x_star[None,:] #データ点と任意のx_starを全ての距離をnumpyのBroad castで計算している
Dist = np.square(Delta)
H = np.exp(-0.5/sigma * Dist) #近傍半径が大きいほど、距離をあまり考慮しなくなるのがわかる
G = np.sum(H, axis=0)[None,:]
R = H/G
check_sum = np.sum(R, axis=0)
# print(check_sum)
Y = R.T@t #(任意のx_starの数,データ数) x_star (データ数, ラベルの次元(今回は1))
sigma = 0.2 #近傍半径
NW(sigma)
↑ 式の実装をミスっていました. 5行目のHの実装のところのsigmaは正しくはsigma** 2です.
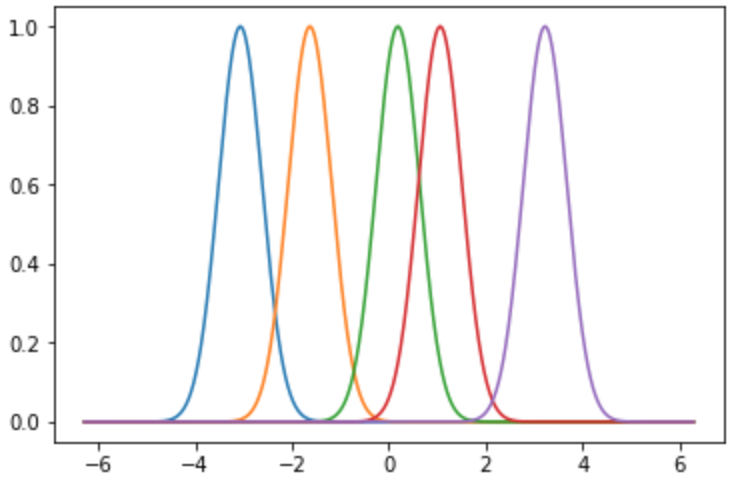
カーネル関数:
f(\mathbf{x}) = K_\lambda(\mathbf{x},\mathbf{x}_i):
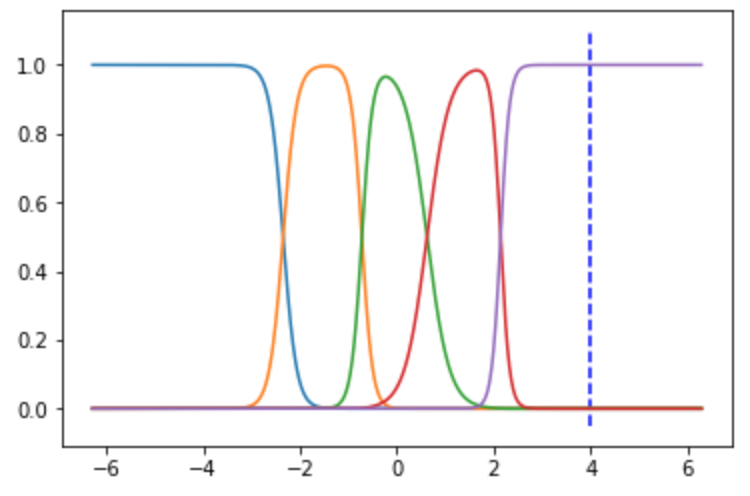
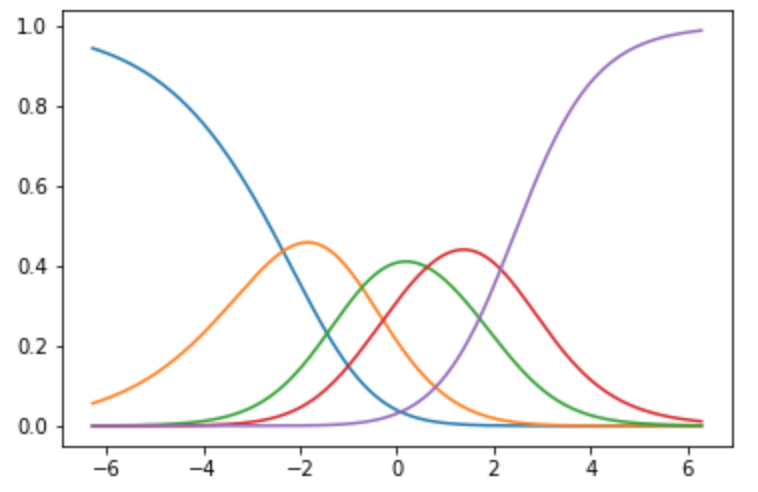
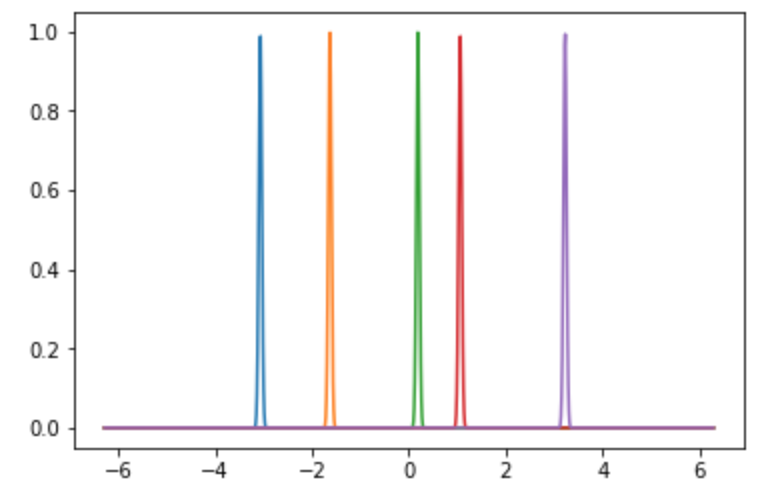
各データ点$x_i$を中心とした近傍半径0.2のガウス関数が描画されました.
各ラベルが及ぼす範囲を可視化したものと思ってよいでしょう.着目点(任意の$x$)で
例えば,任意の$x$を$x=4$としたとき,紫のガウス関数が他のデータ点よりも大きくなっています.
つまり,x=4の写像f(x)の値は紫のデータ点$x_{purple}$に対応するラベル$y_{purple}$の重みを他のラベルよりも大きく用いるつもりのようです.
カーネル関数:
f(\mathbf{x}) = \frac{K_\lambda(\mathbf{x},\mathbf{x}_i)}{\color{red}{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}}:
任意の$x$において全ての重みの合計が1となるように 正規化(カーネル関数なので元から $0 < x \leqq 1$ でした.) 処理をします.
着目点(青点線 $x=4$)を見ると, 総和が1(紫の関数がほぼ1)になっていることがわかりやすいと思います.
x<4でも紫の関数がほぼ1になっています.この処理をすることによって,$f(x) \simeq 1 * x_{purple}$ となって,x<4のとき,$f(x) \simeq x_{purple}$となるわけですね.
重み付きカーネル平均:
f_{NW}(\mathbf{x}) = \frac{\color{red}{\sum_{i=1}^N} K_\lambda(\mathbf{x},\mathbf{x}_i) \color{red}{y_i} }{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}
最終的なNadaraya-Watson推定における式は上式になります.
f_{NW}(\mathbf{x})= {\sum_{i=1}^N} r_i(\mathbf{x}) {y_i} \\
r_i(\mathbf{x})= \frac{K_\lambda(\mathbf{x},\mathbf{x}_i)}{{\sum_{j=1}^N K_\lambda(\mathbf{x},\mathbf{x}_j)}}
これを上のようかけば,ある重み$r_i$でy_iをかけてその総和をとったものがfということがわかると思います.
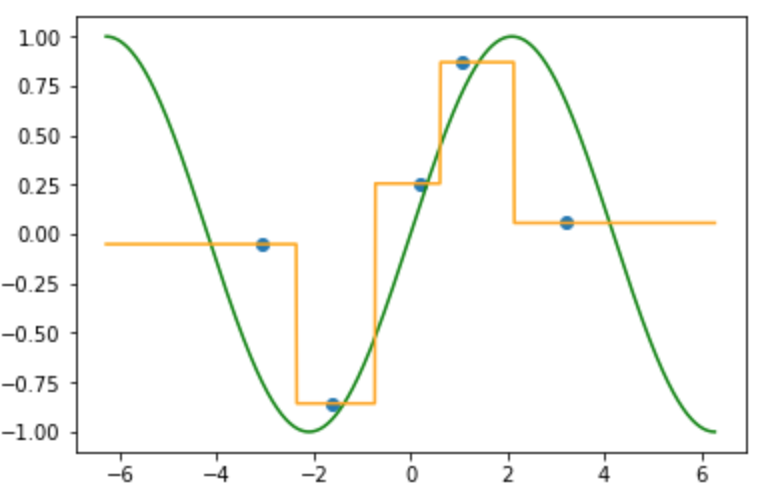
先ほどのカーネル関数でそれぞれのラベルに重みをつけ 総和をとったもの(総和が1なので重み付き平均)が推定した写像(オレンジ線)です.
k近傍法と同様にデータの内分点を通り, 得られた写像は滑らかな写像になっていることが確認できます. またデータの端点以降($x > -3.0, 3.3 < x$)の写像は端点のラベルに収束しています.
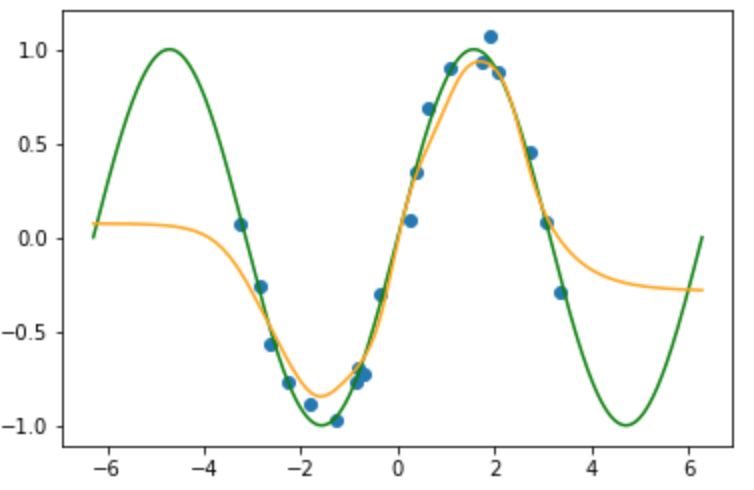
データ数を増やした場合以下のような結果になります.
データ数の数ほどガウス関数を用意しているので, データ数の数ほど表現力があがることになります.
次に近傍半径の大きさを変えた実行結果を見ていきましょう.
近傍半径: 2.0のとき
近傍半径を大きくした場合, 任意の$x$ではより遠くのデータの影響を受けやすくなります.
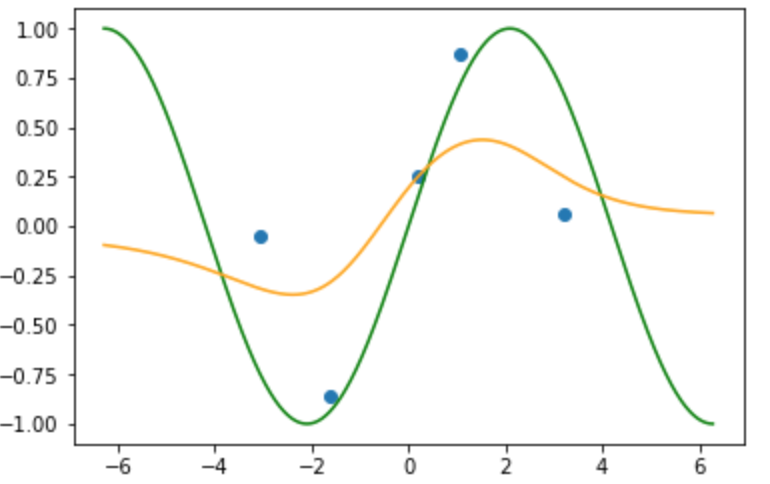
限りなく近傍半径を大きくした場合写像は単純にラベルのほぼ平均になります.
近傍半径: 10000.0のとき
(そういえばk近傍法も$k=n$のときラベルの平均になったなあ....あれれ??)
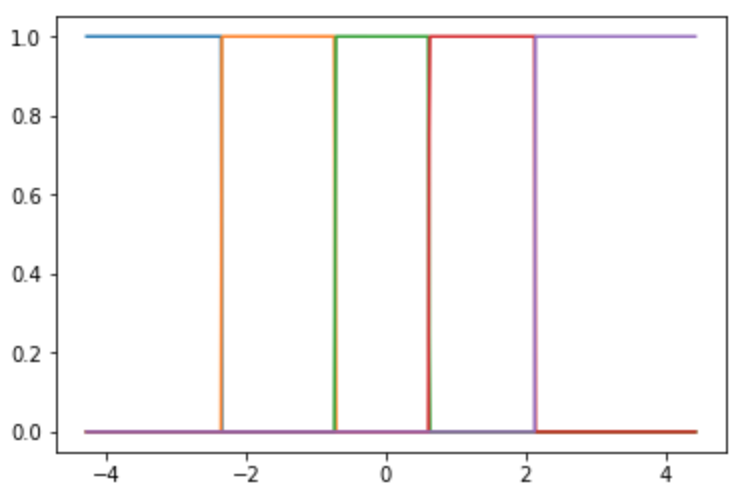
近傍半径: 0.001のとき
近傍半径を小さくした場合, 任意の$x$で他のデータの影響を受けにくくなります.
カーネル関数はデルタ関数のようになります.
任意の$x$では, ほぼ一つの点にしか重みがついてないことがわかります.
k近傍法(k=1)
ここで近傍法との関わりを見ていきましょう.
近傍の数が1の時の結果は以下のようになります.
NWで近傍半径の大きさを限りなく小さくした時と同じような結果になりました.
今回は近傍の数が1の場合でしたが,1以外の場合のk近傍法をあえてカーネル回帰として捉えるならば, 近傍が変わるまでの長さが一律ではないことから, カーネル幅がデータごとによって変わるデジタル波形のような関数をカーネル関数としたカーネル回帰といえそうです.?
まとめ
Nadayawa-Watson推定はk近傍法と違い,滑らかな写像が推定できることがわかりました.どちらの手法もラベルを使って写像を表現するということは変わらず どちらもデータの内分点を通るような写像で, 近傍半径を変えることによってその写像の様相は変化します.
実行ソース
Google Colab
Github
ここにあげているのでよければ実行してみてください.
参考文献
Trevor Hastie・Robert Tibshirani・Jerome Friedman著, 杉山 将・井出 剛 ら監訳 「統計的学習の基礎」 $\S 6$ p.220~