| 逐次学習なし | 逐次学習 | |
|---|---|---|
| 予測 | 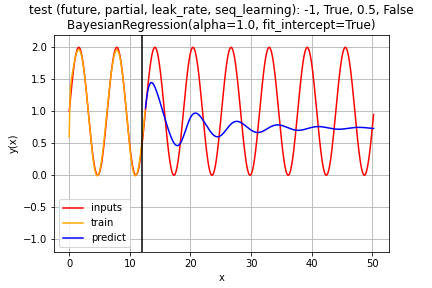 |
 |
はじめに
リザバーコンピューティング(Reservoir Computing) を、逐次学習 (sequential learning)で動かしてみました。
逐次学習は、ベイズ線形回帰で実装しています。
リザバーコンピューティングとして、Leaky Integrator Echo State Network(LI-ESN)を実装しています。
リザバーコンピューティングは、シンプルな回帰型ニューラルネットワーク(RNN:Recurrent Neural Network)で、時間パターンの処理ができ魅力的です。
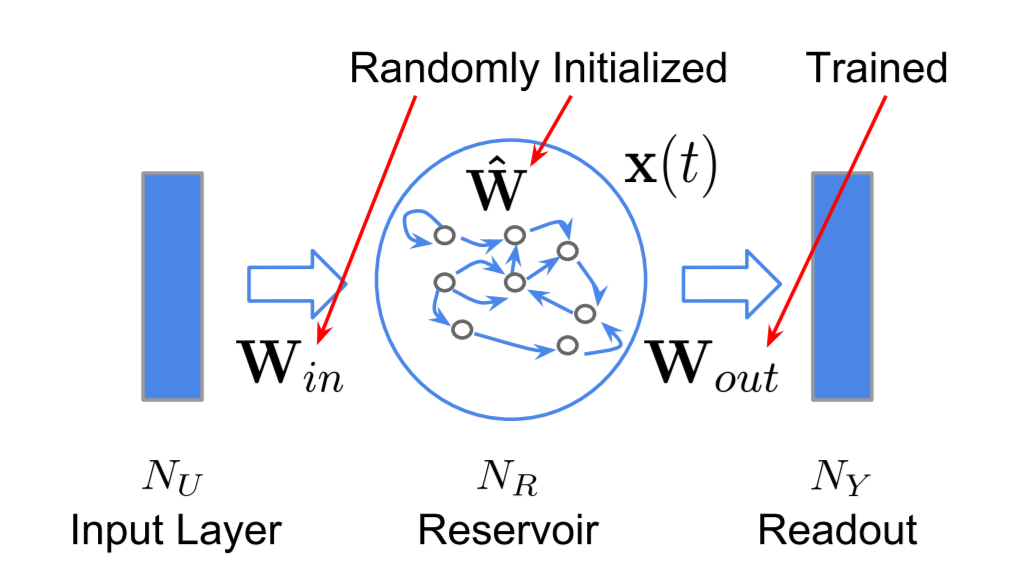
リザバーの計算式
時刻を $t$ としたとき、リザバーの状態 $x$ 、出力 $y$ の計算式を次に示します。
x(t+1) = f_{activator}\biggl((1 - \delta)x(t) + \delta\Bigl(W_{in}u(t+1) + W_{res}x(t)\Bigr) \biggr)\\
y(t) = W_{out}x(t) \\
ここで、$u$ は入力、$δ$ は漏れ率を示します。
$W_{in}$、$W_{res}$、$W_{out}$ は、それぞれ、入力、リザバー状態、出力を計算する重みです。
$W_{in}$、$W_{res}$ は、初期化時にランダムに設定して固定です。
$W_{out}$ は、ベイズ線形回帰で、逐次更新します。
「Deep Reservoir Computing」 Figure 2.7: The ESN architecture より
https://etd.adm.unipi.it/theses/available/etd-02282019-191815/unrestricted/Deep_Reservoir_Computing.pdf
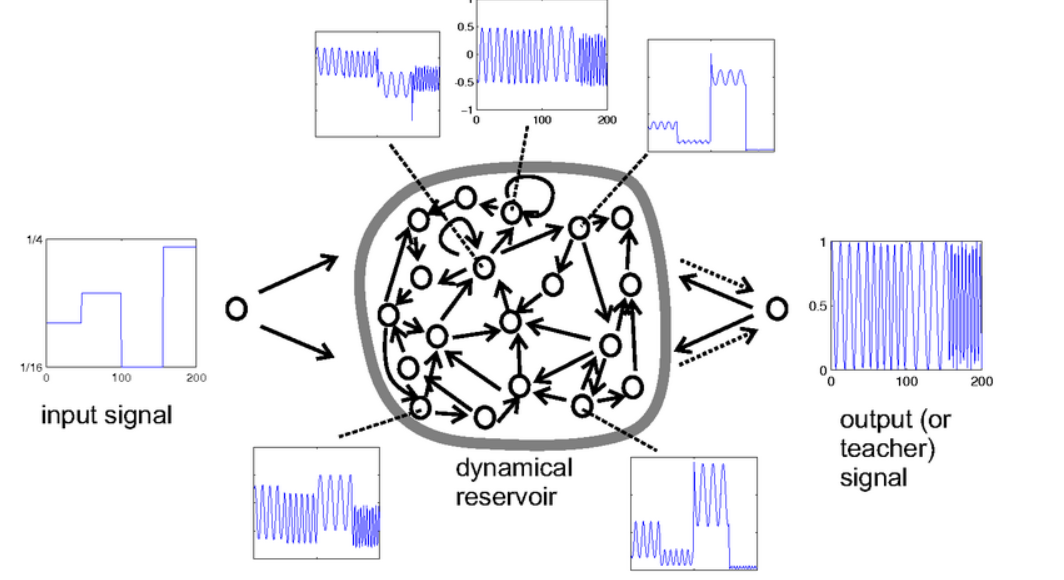
次の図は、tuneable frequency generator task の例です。
「Echo state network」Figure 1 より
http://www.scholarpedia.org/article/Echo_state_network
実行結果
入力 $sin(t)$ に対して、教師データ $sin(t+future)$ で学習させました。 future は予測時間です。
学習後のテストフェーズでは予測した値を入力データに戻して使用します。
予測結果は、漏れ率、予測時刻により大きく変化します。
逐次学習無し
学習フェーズでは、入力(赤)から予測(黄色)をうまく出力しています。
テストフェーズでは、時刻が経過するにつれて、予測(青)の振幅が小さくずれていきます。
位相のズレも拡大しています。
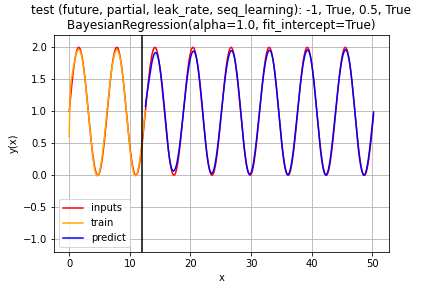
逐次学習有り
テストフェーズでは、時刻が経過しても、予測(青)の振幅と位相が維持できています。
プログラム
プログラム環境
matplotlib 3.2.1
numpy 1.18.2
scikit-learn 0.22.2.post1
scipy 1.4.1
Python 3.6.9
Reservoir クラス
class Reservoir:
def __init__(self, node_n, leak_rate=0.1, reg=linear_model.Ridge, activator=np.tanh, W_res_file=None): # 'W_res.npy'
self.node_n=node_n; self.leak_rate=leak_rate; self.reg=reg; self.activator=activator # (in, res, out)
self.State = np.array([np.zeros(self.node_n[1])]) # Log for Ridge Regression
self.W_in = (np.random.randint(0, 2, node_n[0]*node_n[1]).reshape([node_n[0], node_n[1]]) *2 -1) * 0.1
if W_res_file and os.path.isfile(W_res_file): self.W_res = np.load(W_res_file)
else:
_weights = np.random.normal(0, 1, node_n[1] * node_n[1]).reshape([node_n[1], node_n[1]])
_spectral_radius = max(abs(linalg.eigvals(_weights)))
self.W_res = _weights / _spectral_radius
if W_res_file: np.save(W_res_file + '.out', self.W_res)
def _next_state(self, input, current_state):
return self.activator((1.0-self.leak_rate)*current_state + (self.leak_rate * (np.array([input])@self.W_in + current_state@self.W_res)))
def fit(self, X, T):
for i, input in enumerate(X):
current_state = np.array([self.State[-1]])
self.State = np.append(self.State, self._next_state(input, current_state), axis=0)
self.State = self.State[1:]
self.reg.fit(self.State, T)
def partial_fit(self, X, T):
for i, input in enumerate(X):
current_state = self.State[-1]
self.State = self._next_state(input, current_state)
self.reg.partial_fit(self.State, np.array([T[i]]))
def predict(self, X, init_state=False, update_state=False):
outputs = []
reservoir_nodes = np.zeros(self.node_n[1]) if init_state else self.State[-1]
for x in X:
reservoir_nodes = self._next_state(x, reservoir_nodes.reshape((self.node_n[1],))) #.reshape((150,))
outputs.append(self.reg.predict(reservoir_nodes))
if update_state: self.State = reservoir_nodes
return np.array(outputs)
ベイズ線形回帰クラス
class BayesianRegression():
def __init__(self, alpha=1.0, sigma=0.2, fit_intercept=True):
self.lambda_ = alpha
self.sigma = sigma # noise standard deviation
self.fit_intercept = fit_intercept
self.M = 0 # len(w)
self.w, self.intercept_, self.coef_, = None, None, None
self.m, self.S = None, None # mean, variance
self.beta = 1.0 / (self.sigma ** 2) # precision
self.alpha = self.lambda_ * self.beta
if self.alpha == 0.: print("set alpha=0.001 (Prevent division by zero)")
def fit(self, X, T):
self.partial_fit(X, T)
def partial_fit(self, X, T):
if (self.fit_intercept): X = np.insert(X, 0, 1., X.ndim-1)
if self.M==0 and len(X)>0: # Initialize
self.M = (len(X[0]),len(T[0]))
self.m = np.zeros((self.M[1], self.M[0]))
self.S = np.array([np.identity(self.M[0]) / self.alpha]*self.M[1]) # (3.52)
for j in range(len(T[0])): # out nodes loop
for i in range(len(X)): # data loop
phi, t = np.array([X[i]]), T[i]
phi_T = phi.T
S_inv = np.linalg.inv(self.S[j])
self.S[j] = np.linalg.inv(S_inv + self.beta * phi_T @ phi) # (3.51)
self.m[j] = (self.S[j] @ ((S_inv@self.m[j]).reshape(-1,1) + self.beta * phi_T * t[j])).reshape(-1,) # (3.50)
self.w = self.m
if (self.fit_intercept): self.intercept_, self.coef_ = self.w[0], self.w[1:]
else: self.intercept_, self.coef_ = 0, self.w
def predict(self, X):
if self.fit_intercept: X = np.insert(X, 0, 1, X.ndim-1)
return X @ self.w.T
テストプログラム
%matplotlib inline
from scipy import linalg
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
def test(constructor, future, t_fn=np.sin, leak_rate=0.5, seq_learning=True, partial=False, x_n=1000, train_ratio=0.25, y_amp=1.0):
title = "test (future, partial, leak_rate, seq_learning): "+ str(round(future, 2)) + ', ' + str(partial) + ', '+ str(leak_rate) + ', ' + str(seq_learning)
def graph_out(x, y, x_train, train_result, x_test, predict_result, x_border):
plt.plot(x, y, label="inputs", color="red")
plt.plot(x_train, np.array(train_result).flatten().tolist(), label="train", color="orange")
plt.plot(x_test, np.array(predict_result).flatten().tolist(), label="predict", color="blue")
plt.axvline(x_border, color="black") # border of train and prediction
plt.legend(); plt.legend(loc="lower left"); plt.grid(); plt.ylim(y_min, y_max)
plt.xlabel("x"); plt.ylabel("y(x)"); plt.title(title + '\n' + constructor)
plt.savefig(constructor + title + '.png'); plt.show()
x_delta = np.pi*16
x_min, x_max, y_min, y_max = 0, x_delta, -1.2, 2.2
x_border = int(x_delta*train_ratio + x_min)
future_n = max(1,int(future/(x_delta/x_n))) if future > 0 else - future
x = np.linspace(x_min, x_max, x_n)
y = t_fn(x).reshape(-1, 1) * y_amp
train_n = int(x_n * train_ratio)
x_train, x_test = x[:train_n], x[train_n: - future_n]
y_train, y_test = y[:train_n], y[train_n: - future_n]
t_train, t_test = y[future_n: future_n+train_n], y[train_n+future_n:]
x, y, test_n = x[:-future_n], y[:-future_n], len(x_test)
model = Reservoir(node_n=(1, 150, 1), reg=eval(constructor), leak_rate=leak_rate)
if partial: model.partial_fit(y_train, t_train)
else: model.fit(y_train, t_train)
train_result = model.predict(y_train, init_state=True, update_state=False)
predict_result = train_result[-future_n:]
for _i in range(test_n ):
if seq_learning: model.partial_fit(np.array([y_test[_i]]), np.array([t_test[_i]]))
tmp = model.predict(np.array([predict_result[-future_n]]), init_state=False, update_state=True)[0].flatten()
predict_result = np.append(predict_result, [[tmp]], axis=0)
predict_result = predict_result[future_n:]
graph_out(x, y, x_train, train_result, x_test, predict_result, x_border)
if __name__ == '__main__':
def init(): np.random.seed(0)
t_fn = lambda x: np.sin(x) +1.0
# future = np.pi/4
future = -1
leak_rate = 0.5
init(); test('BayesianRegression(alpha=1.0, fit_intercept=True)', future, t_fn, leak_rate, partial=True, seq_learning=False)
init(); test('BayesianRegression(alpha=1.0, fit_intercept=True)', future, t_fn, leak_rate, partial=True, seq_learning=True)
!ls -lt
参考資料
リザバー(Reservoir)に意識は宿るか?(記憶、概念獲得、判断、予測)
https://qiita.com/tshimizu8/items/41945567730a840e8cc1
ベイズ線形回帰ってナンだ?(Bayesian linear regression)
https://qiita.com/tshimizu8/items/e5f2320ce02973a19563
Echo state network
http://www.scholarpedia.org/article/Echo_state_network
Deep Reservoir Computing
https://etd.adm.unipi.it/theses/available/etd-02282019-191815/unrestricted/Deep_Reservoir_Computing.pdf