前回までの課題
- 状態価値関数$V^\pi(s)$、行動価値関数$Q^\pi(s,a)$を定義に従って求めた (第1回,[ 第3回)] (https://qiita.com/triwave33/items/8966890701169f8cad47)
- 無限回の再帰処理(枝分かれ探索)が必要だが、実用的には計算を打ち切る必要があった
- 値が収束せず、計算時間もかかった (第2回)
- 無限回の再帰処理(枝分かれ探索)が必要だが、実用的には計算を打ち切る必要があった
- 価値関数を比較することで方策を改善することができ、ある状態で最適な行動を決められた [(第4回)] (https://qiita.com/triwave33/items/669a975b74461559addc)
- その際、価値関数の計算時間の遅さがネックになる
今回わかること、できること
- 価値関数を近似して反復的に解く
- 価値関数の初期値を適当に設定し、繰り返し更新していく
今回行ったこと
- 定義通りの(再帰的な)価値関数の計算と(反復的な)近似価値関数の比較
- 価値関数近似の解説
問題設定
第1回で説明した格子世界
Aにいる状態でどんな行動をとっても+10点、Bも同様に5点。壁にぶつかると-1点

結果
まずは定義通り、再帰的に価値関数を求めたときの、5x5マスの状態価値関数のプロットです。
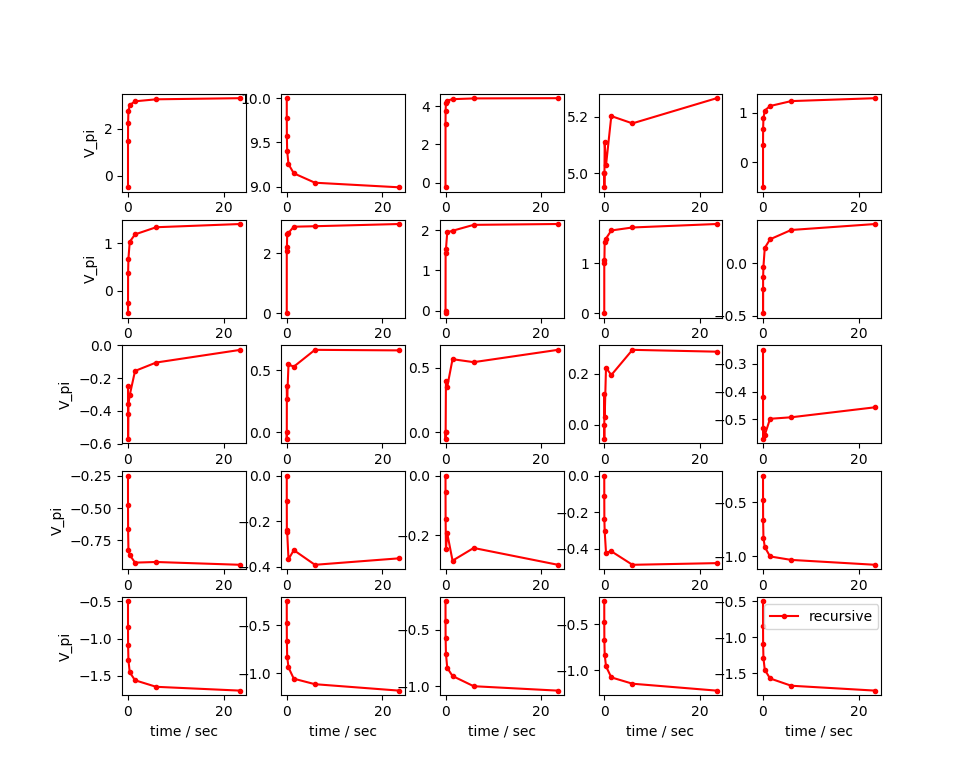
横軸は時間(秒)を表しており、約20秒で8回の再帰処理をおこなっています。
組み合わせは各状態に対して$4^8 = 65536$通り、全体に対しては$4^8\times25 = 1,638,400$通りです。
マスによってはまだ収束しているとは言い難いですね。試行回数に対して指数関数的に計算時間がかかります。
次に反復による近似計算の結果を示します。
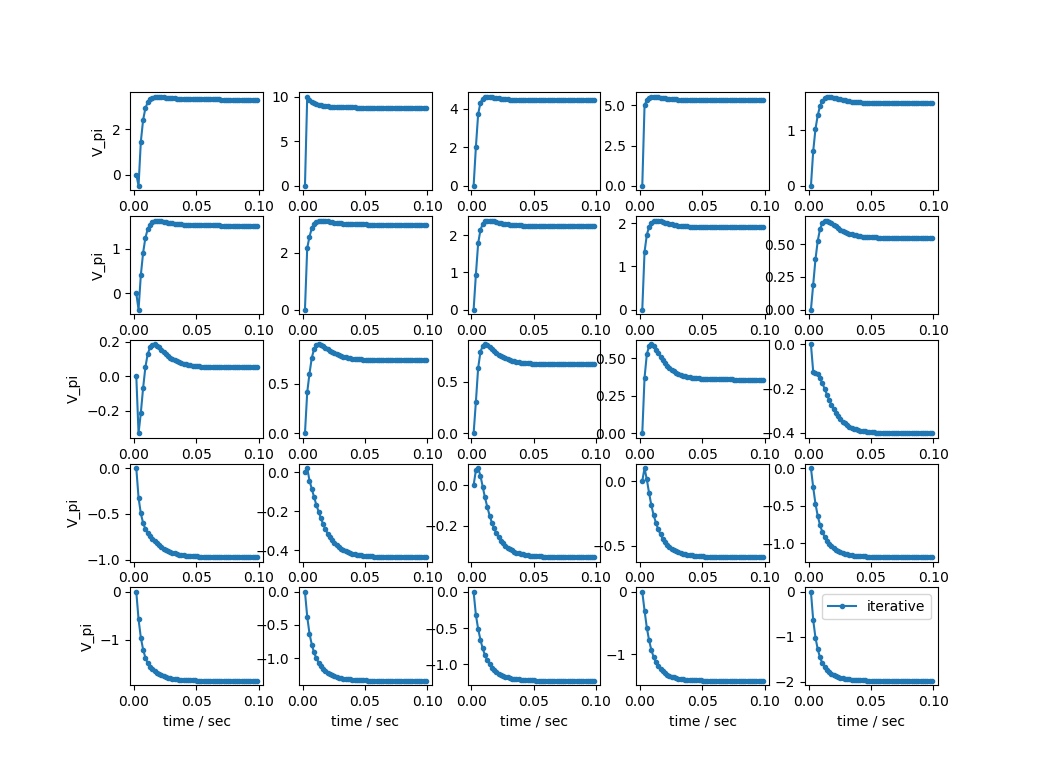
横軸は先ほどと同じです。0.1秒以内に収束しています。圧倒的に早いですね。
二つの図を重ねようと思っていたのですが、重ねると横軸のレンジが違いすぎてよくわからなくなったので、別々にしました。
ということで、定義通り再帰的に状態価値関数を求めるよりも、近似により反復的に求めるほうが収束も早く、計算量も少なくてすみます。
ということで、価値関数の計算はこの反復方法を使うこととします。
以下では、バックアップダイアグラムと合わせて、どのように計算を行っているかを再帰的方法との違いを示しながら解説します。
再帰処理と反復処理の違い
再帰処理
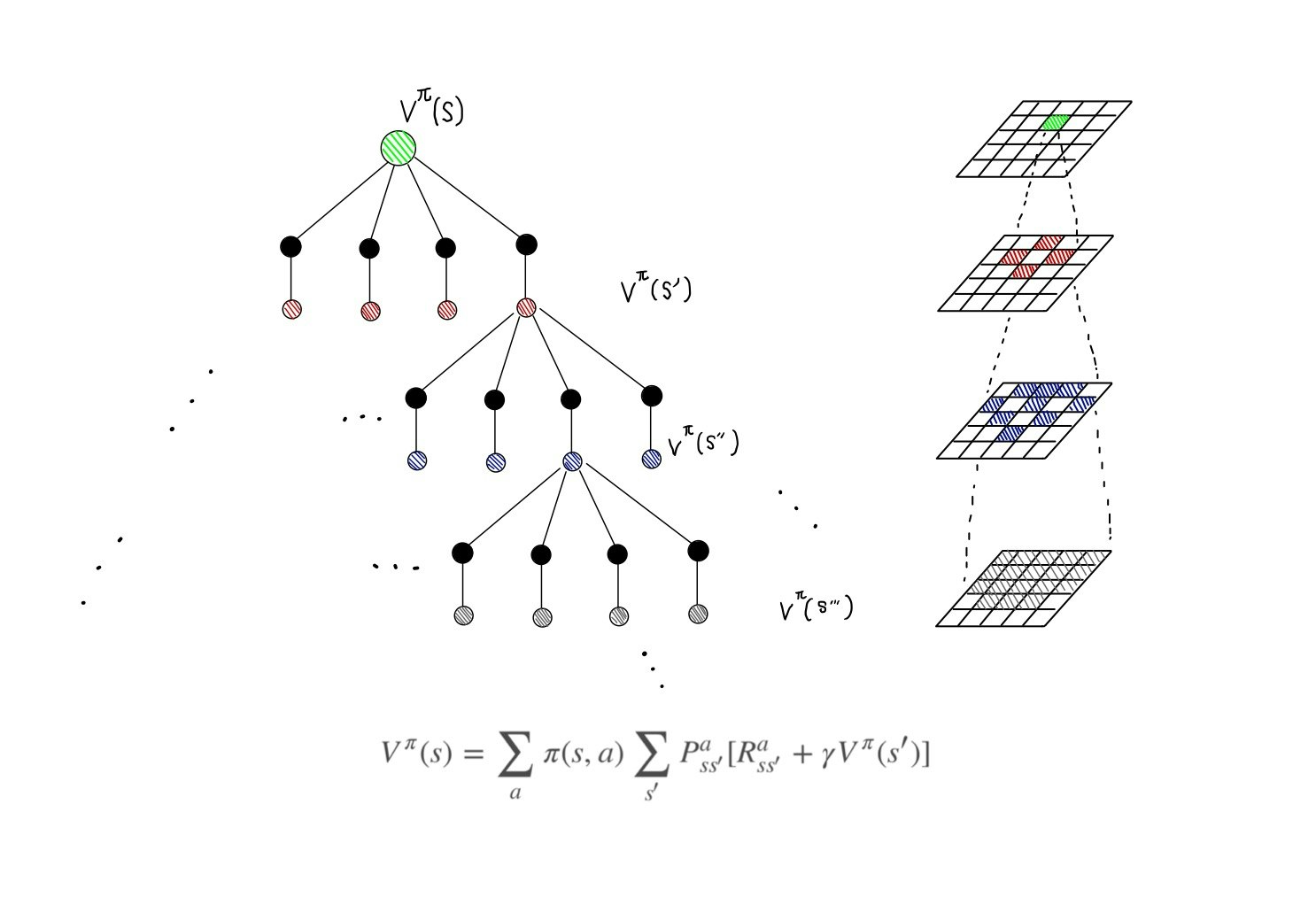
まずは、定義通り状態価値関数を再帰的に求めていく処理を図説します。$V^\pi(s)$(図中の緑丸)を求めたい場合は、この状態から、取り得る行動に対して枝分かれをします(黒丸)。上下左右なので4本に枝分かれします。
次に緑丸から黒丸の行動をとった時、次の状態に遷移します(赤丸)。この例の場合、行動に対する状態は一意に確定的に求まりますので、枝分かれはしません。複数の状態に確率的に遷移する場合は枝分かれします。
さて、緑丸を求めるためには赤丸を求める必要があります。赤丸を求めるためには、赤丸から取り得る行動(黒丸)をとった先に落ち着く状態(青丸)を求める必要があります。
このように、とりうる状態、行動、その結果落ち着く状態を考慮しつつ、エピソードを再帰的に掘り進めて処理をしていく必要があります。エピソードに終端状態(ゲームエンド)がある場合はそこで打ち止めですが、この問題設定の場合、終端状態はないので理屈上は永遠に計算する必要があります。
実用的には収束するまで繰り返せばいいのですが、一番最初に見せた図のように計算時間がかかり収束しません。
高々25個の状態と4個のアクションでこんなにかかるのであれば、もっとも状態数、行動数が多い時にうまくいかないのは自明です。
反復処理による近似
その解決作として、高速な反復方法を示します。
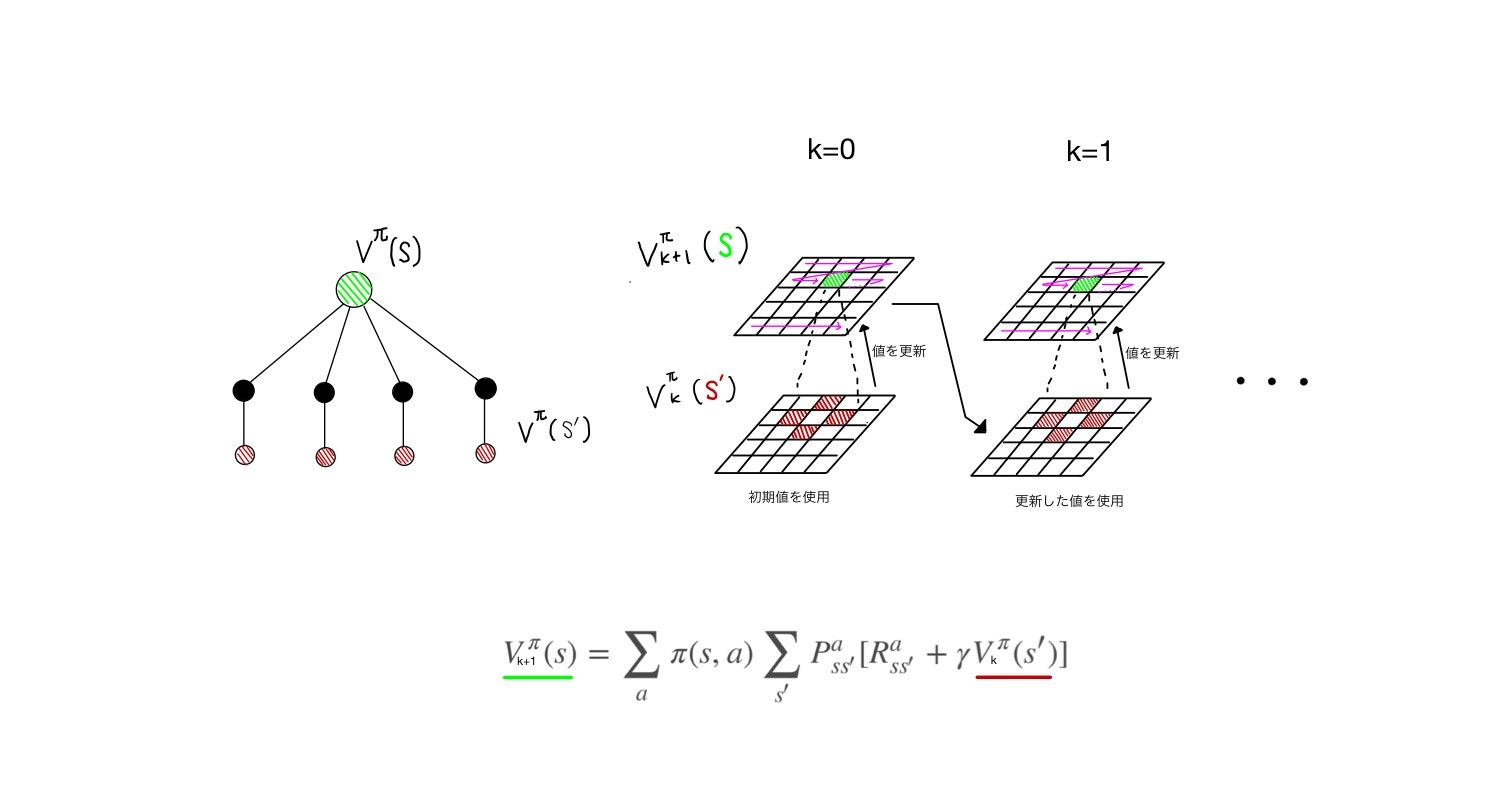
左に書いたバックアップダイアグラムをみると、再帰的な方法との差がよくわかると思います。**反復近似方法では、今の状態とその先の状態の2層しか考えません。**そのかわり、この2層計算を値を更新しつつ反復して繰り返します。
まず価値関数に適当な初期値を入れておきます。全てゼロでよいでしょう。緑丸の価値関数を求めたい場合、その先の行動によって取り得る状態(赤丸)の価値を使って計算を行います。赤丸の値は初期値のゼロを用います。これにより、初回の反復時の緑丸の状態価値が求まります。
k=0の上の層の緑部分以外のところも同様にして値を更新します。それを図では紫色の矢印のスイープで表しています。
k=0の上層で状態空間全体に対して更新した結果を、次の反復ステップ(k=1)の下層に移動させます。それを用いて、また状態価値(上層の緑)を更新していきます。これを繰り返すことで値をゼロから反復的に更新させていきます。
枝分かれが2層間でしか発生しないので計算処理が圧倒的に早くなり、反復回数をこなす必要があることを差し引いても組み合わせ爆発する再帰処理よりも早く収束します。また、この反復により$k\rightarrow\infty$の極限で$V^\pi$に収束することが一般的に示されます。
このアルゴリズムを方策反復評価と呼びます。
反復的方法の際の式を図の下に書いています。添字$k+1$,$k$以外は$V\pi(s)$の定義(さらに上の図の式)と変わりませんが、実際の求め方はこのように異なります。
実は、定義式から再帰的に解く方法の他に、状態数と同じ個数の連立方程式を解析的に解くやり方もあるようなのですが、ここでは説明しません。別の問題設定ですが、詳細は後述する参考文献のP.84に出ています。
方策反復評価アルゴリズム
最後にSutton本(Richard S. Sutton and Andrew G. Barto 強化学習、森北出版 P.97)に記載の反復方策評価アルゴリズムを引用します。
評価対象の方策$\pi$を入力
すべての$s \in S^+$に対して$V(s) = 0$とする
繰り返し:
$\Delta \leftarrow 0 $
各$s \in S$について:
$v \leftarrow V(s) $
$V(s) \leftarrow \sum_a\pi(s,a)\sum_{s'}P^a_{ss'}[R^a_{ss'} + \gamma V(s') $
$\Delta \leftarrow max(\Delta, |v-V(s)|)$
$\Delta < \theta$(正の小さな値)ならば、繰り返しを終了
$V \approx V^\pi $を出力
これにしたがって、最初に上げた青色のプロットを求めました。
「その場更新型」バックアップ
反復処理を上図の説明通り実行するためには、上層の配列を下層の配列を二つ持っておいて、上層のスイープを完全に終了してから下層に代入し、さらに次の反復ステップへと進む必要があります。これにより、元の価値に影響を与えずに新しい価値を元の価値から次々と計算することができます。
別の方法として、配列を一つだけ使って次々に更新することもできます。つまり、スイープの途中で値が更新されていってしまうので、次のスイープの状態(隣)の価値を更新する場合、元の価値はすでにその値を保っていないことになり得ます。Sutton本(P.96)を引用すると、
このアルゴリズム(注:その場更新型バックアップのこと)は以前のものと少し異なっているが、同じく$V^\pi$に収束する。実際、得られた新しいデータをすぐに利用するので、このアルゴリズムは通常は早く収束する。
(省略)
「その場更新型」のアルゴリズムでは、スイープ操作を通じ、状態がバックアップされる順序が収束の速度に大きな影響を及ぼす。
とあります。まぁ考えたら当たり前ですが、スイープの順番が影響を及ぼすことは覚えておいた方がいいですね。
ちなみに上記のアルゴリズムは、「その場更新型」のバックアップになります。