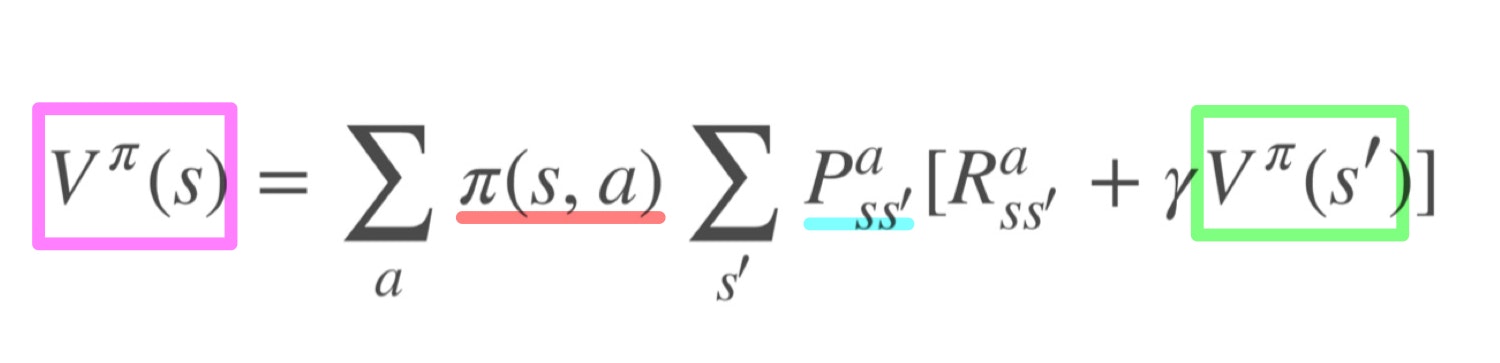はじめに
これまで6回に渡り、強化学習の基礎知識を説明してきました。ある決められた世界(格子世界)に対して、状態sをとること、もしくは状態sのときに行動aをとることの価値を算出しました。
今さら聞けない強化学習(1):状態価値関数とBellman方程式
今さら聞けない強化学習(2):状態価値関数の実装
[今さら聞けない強化学習(3):行動価値関数とBellman方程式] (https://qiita.com/triwave33/items/8966890701169f8cad47)
[今さら聞けない強化学習(4):行動価値関数の実装] (https://qiita.com/triwave33/items/669a975b74461559addc)
今さら聞けない強化学習(5):状態価値関数近似と方策評価
[今さら聞けない強化学習(6):反復法による最適方策]
(https://qiita.com/triwave33/items/59768d14da38f50fb76c)
今回からはこの方法の問題点と、それを解決するための手法の一つであるモンテカルロ法について説明していきます。まずおさらいとして、下図のバックアップ線図(ダイアグラム)を示します。

状態$s$から方策$a$をとり、状態$s_{t+1}$に遷移して報酬$R_{ss'}^a$を得るという1ステップの状態遷移が描かれています。この状態遷移には、取れる行動の数だけの選択肢(枝分かれ)があります。また行動$a$を取った後の状態はただ一つに確定的に決まるわけではありません。ある確率分布を持って複数の状態のうちのどれかに落ち着きます。
状態$s$の時に行動$a$をとる確率は$\pi(s,a)$で決まり、この$\pi$を方策と呼びました。また、状態$s$の時に行動$a$を取った時に$s'$に遷移する確率を$P_{ss'}^a$と表します。
この枝分かれは、エピソードの終着点(ゲームエンド)まで繰り返されますし、終着点がない場合は無限に繰り返されます。
方策$\pi$に従った時の状態$s$の価値は
と表されます。(詳しくは第1回を参照)。つまり、ある状態の価値はその後の状態の価値を用いて表すことができるということです。これをブートストラップとよびます。状態関数のブートストラップ性を利用して、状態価値関数を反復的に求めることができました。(第5回)。また、それを元に最適な方策を決めることができました(第6回)
このように、枝分かれをその確率値に従って辿り、価値を計算しました。このような手法を動的計画法と呼びます。
動的計画法の計算の意味
上式の$[R_{ss'}^a + \gamma V^\pi(s')]$は、枝分かれを進んでいって終着点にたどり着くまでの報酬の総和です。$\sum_a \pi(s,s)$および$\sum_{s'}P_{ss'}^a$は、各枝分かれの確率とそれに応じて取り得る報酬を掛けて足し上げています。つまりこれは、全ての枝分かれを考慮した報酬の期待値に他なりません。
動的計画法の問題点
価値関数および最適方策を求めることができる動的計画法ですが、ある原理的な制約があります。それは、環境のダイナミクスが既知であることです。端的に言えば、$P_{ss'}^a$が完全にわかっているということです。($\pi(s,a)$もわかっている必要もありますが、こちらは自分で決めることもできるので)
もう少し具体的に説明しましょう。例えば、これまでの記事で問題にしてきた格子世界では、右に動けばどこに行くかということが完全にわかっていました。何も制約がなければ、右に動けば右のマスに進みますし、壁に当たれば進みません。AやBにいればワープしました。このように、系の知識が完全にわかっている、すなわちゲームのルールを完全に把握しています。
しかし、現実世界ではこれが常に成り立つとは言えません。車を動かすためにハンドルを右に切ったとしても、その結果どのような状態に落ち着くのかは、天候や路面状態、車両重量などでその都度違うでしょう。また、人間はそれを完全に理解していません。
自然の法則から神様は知っているかもしれませんが、その状況を完全にモデリング(把握)して動的計画法で解くのは現実的ではありません。そもそも、系の知識が完全にわかっているなら必ずしも強化学習で解く必要はありません。
代替案としてのモンテカルロ法
それでは環境のダイナミクスについて知らなくても、行動の結果得られた報酬から価値を推定し、最適な方策を求める方法はないのでしょうか。幸いなことに複数の方法があります。そのうちの一つが今回説明するモンテカルロ法です。
強化学習におけるモンテカルロ法では、エピソードに従ってエージェントに行動を取らせ報酬を得ます(サンプリング)。各状態に対して、実際に取られた報酬の平均をとることで期待値を計算します。
- モンテカルロ法
- サンプリング
- 期待値
のイメージを次章で説明します。(強化学習とは関係ありません)
モンテカルロ法のイメージ
モンテカルロ法をイメージするために、以下のような原点中心、半径0.5の円の面積を求める問題を考えます。強化学習っぽく、円の面積を求めるゲームと考えましょう。
このゲームについて、環境のダイナミクスを理解するとは(やや観念的ですが)、円の面積の公式を知っている、ということになります。つまり、
$$ A = \pi r^2$$
ですね。r=0.5なので、$A \simeq 0.785$です。
円の公式を知らないと仮定して、あえてモンテカルロ法で解いてみましょう。この四角形の紙に対してダーツを投げて、円の中に入ったら1点、入らなかったら0点にします。ただし、紙の外に外れたものはノーカウントとし、紙の中に入るようやり直します。とりあえず20投ほど投げてみます。
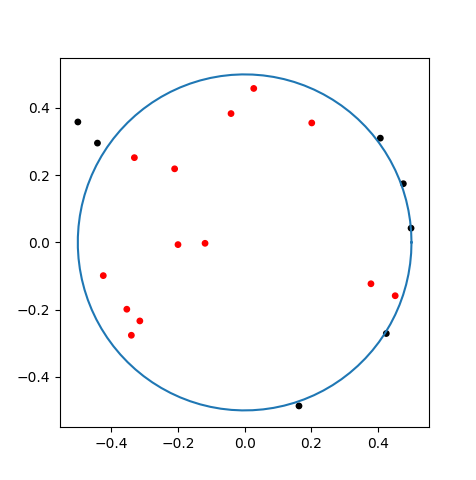
赤丸が円の中、黒丸が円の外ですね。赤が13個入っているので13点です。
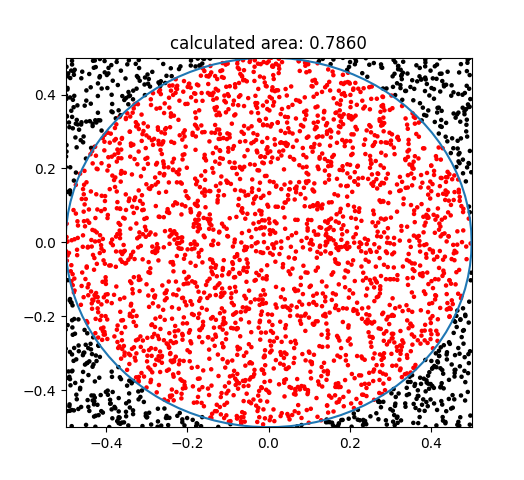
さらに投げて3000回にします。
この場合、赤2358個(点)、黒642個になりました。紙の中を満遍なく投げていますね。さてここから、円の面積を求めてみましょう。
四角計の面積は1、円の面積はAです。点が満遍なく敷き詰められているとすると、面積比は点の個数比に比例すると考えられます。つまり、黒丸の個数を$n_{black}$、赤丸の個数を$n_{red}$とすると
$$ 1 : A = (n_{black} + n_{red}) : n_{red}$$
の関係が成り立ちます。$n_{black} + n_{red}$は試行の総数N=3000ですから、結局
$$ A = 1 * \frac{n_{red}}{N}$$
となり、結果としてこの場合、0.786を得ました。モンテカルロ法では乱数によるサンプリングから求めているので、毎回結果が変わります。強化学習では実際にそのゲームをプレイすれば良いので、どの確率分布から乱数を生成すれば良いのかを考える必要はありません。
動的計画法との対比
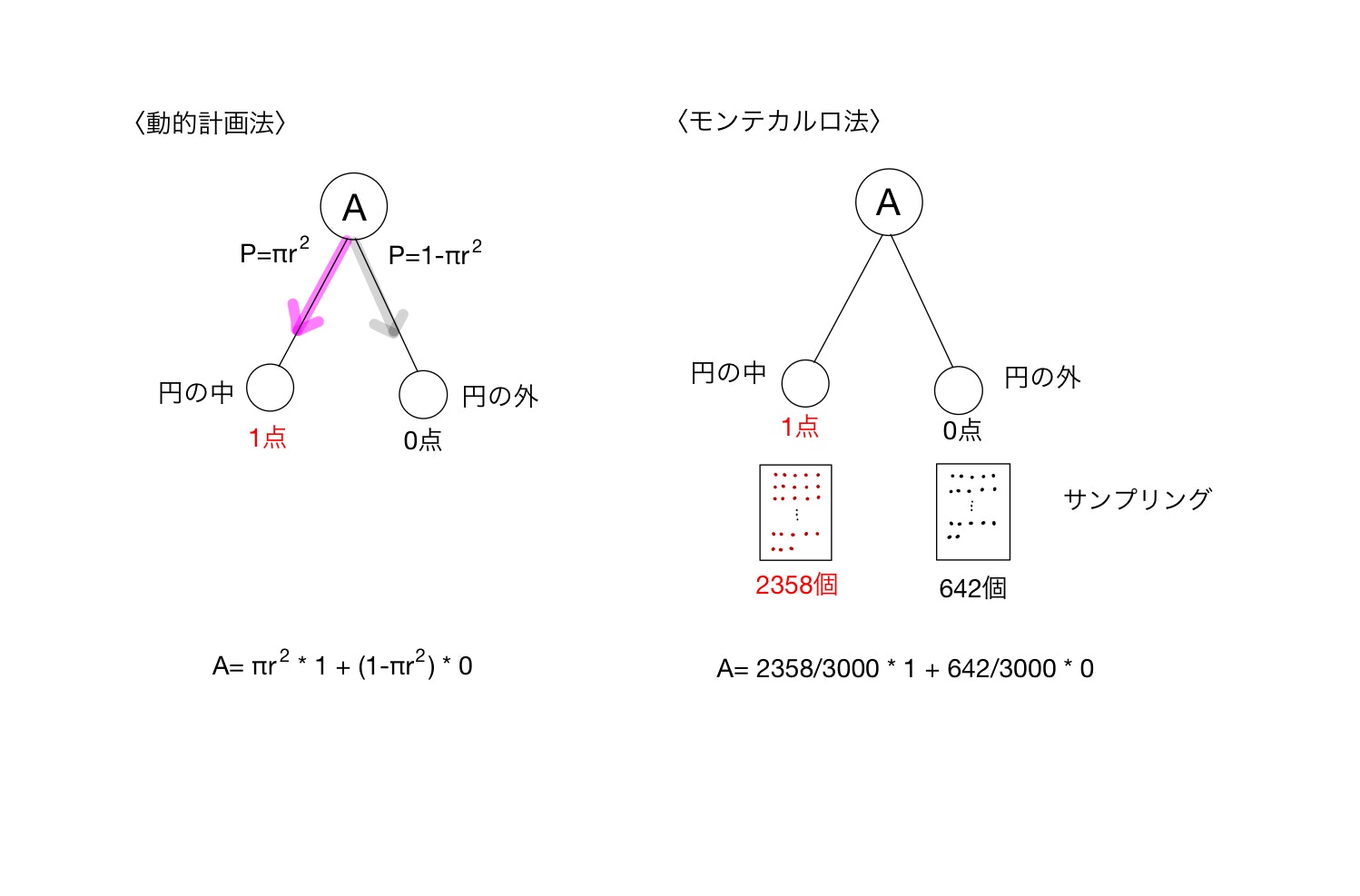
厳密な説明ではなくあくまでイメージですが、円の問題を強化学習のフレームワークに落とし込んで説明します。動的計画法での解き方とモンテカルロ法の解き方を比較したのが以下になります。
解きたい価値は円の面積Aとします。そのために、円の中は1点、円の外は0点と設定して場合分けをしています。「円の中」状態に行く確率は、面積比から$\pi r^2$、「円の外」状態に行く確率は$1-\pi r^2$になります。このように、円の公式を知っていることがこの場合、環境のダイナミクスを知っていることに対応します。枝分かれの確率がわかっているので、実際に得られる報酬を掛け合わせて状態価値である面積Aを得ます。これを見ると、動的計画法は完璧な仕様書を基に机上計算をしているイメージですね。
対してモンテカルロ法の場合、環境のダイナミクス、すなわち枝分かれの確率はわかっていない前提です。分かってはいないのですが、そのダイナミクスに従って物事は進んでいき、結果に反映されます。この場合、円の中と外(と全体)の個数比は枝分かれの確率を反映しているはずですので、ここから得られた確率に報酬を掛け合わせれば価値(面積)が推定されます。このように、モンテカルロ法は説明書は読まずに実際に使って慣れて理解するの精神です。
モンテカルロ法による状態価値推定アルゴリズム。
強化学習における、モンテカルロ法を用いた状態価値推定アルゴリズムのうち、初回訪問モンテカルロ法と呼ばれるアルゴリズムを以下に示します。
初期化:
$\pi \leftarrow$ 評価すべき方策
$V \leftarrow$ 任意の状態価値関数
$Returns(s) \leftarrow$ 空のリスト(すべての$s \in S$に対して)
繰り返し:
(a) $\pi$を用いてエピソードを生成する
(b) エピソード中に出現する各状態sについて:
$R \leftarrow s$ の初回発生後の収益
$R$を$Returns(s)$に追加(append)する
$V(s) \leftarrow average(Returns(s))$
状態$s$から出発して、方策$\pi$にしたがい終端状態までエピソードを進めます。そのエピソードはある遷移確率で枝分かれしていき(例えば上の例では円の中と外)、終端状態で報酬が得られます。得られた報酬を出発状態に対応するリストに追加していきます。最後に得られた収益をリストの長さ、すなわち訪問回数で平均することで価値を算出します。全ての状態について価値を求めるためには、全ての状態を初回開始点にとることが可能である必要があります。
初回訪問モンテカルロ法に必要な条件を下に挙げます。
1.全ての状態を開始点にとることができる
2.エピソードは必ず終端状態を持つ(無限に続かない)
3.経験しない枝分かれ状態があってはならない(全ての状態を無限回訪問する)
格子世界を解く
それでは初回訪問モンテカルロ法を用いて、動的計画法で解いた格子世界の状態価値関数を求めてみましょう。
問題設定
第1回で説明した格子世界
Aにいる状態でどんな行動をとっても+10点、Bも同様に5点。壁にぶつかると-1点、ほかは0点。

格子世界問題が上記の初回訪問モンテカルロ法の条件を満たしているかをチェックします。
まず1の条件ですが、この問題ではエージェントの開始位置を任意に設定できるのでクリアしています。
次に2の条件ですが、この問題には終端状態がないためこの条件を満たしていません。ですので本来はこの問題に初回訪問モンテカルロ法(というよりモンテカルロ法)を使うことができません。苦渋の策として、ステップを100ステップで打ち切ることにしましょう。本来の問題設定とは異なりますが、100ステップ先の収益は割引率$\gamma$が100乗でかかるため、0.0000027倍の寄与率しかありません。ですのでこれくらいまで進めばこれより先は実質無視できるだろうという判断です。
3の条件ですが、今回もとめる状態価値の方策は上下左右ランダムに動くことにしているため、あらゆる状態をとることが満たされます。
実装
実装例を以下に示します。コードはgithubに上げています。
### -*-coding:utf-8-*-
import numpy as np
from itertools import product
import matplotlib.pyplot as plt
from tqdm import tqdm
import grid_world
# agentの生成
agent = grid_world.Agent([0,0])
GAMMA = 0.9
ACTIONS = ['right', 'up', 'left', 'down']
num_row = 5
num_col = 5
num_iteration = 100 # エピソード終了までの反復回数
num_episode = 10000 # MCサンプリング数
# piの設定
def pi(): # 状態sによらない方策
return np.random.randint(0,4) # 上下左右がランダム
# Vの初期化
V = np.zeros((5,5))
# 報酬を格納するリストの初期化
returns = [[[] for c in range(num_col)] for r in range(num_row)]
print("start iteration")
count = 0
N = 100
V_trend = np.zeros((N, num_row, num_col))
for epi in tqdm(range(num_episode)):
delta = 0
i,j = np.random.randint(5, size=2)
agent.set_pos([i,j]) # 移動前の状態に初期化
tmp = 0
for k in range(num_iteration):
action = ACTIONS[np.random.randint(0,4)]
s = agent.get_pos()
agent.move(action) # 移動
s_dash = agent.get_pos() # 移動後の状態
reward = agent.reward(s, action)
tmp += GAMMA**(k) * reward # 移動後の報酬を加算
#print("i: %d, j: %d, s:%s, a:%5s, s';%s" %(i,j, str(s), action, str(s_dash)))
returns[i][j].append(tmp) # indexに注意
#print("count: %d, delta: %f, abs: %f" % (count, delta, abs(v-V[i,j])))
print(V)
returns_length =np.array([[len(returns[r][c]) for c in range(num_col)] \
for r in range(num_row)])
print("length of returns")
print returns_length
returns_average =np.array([[np.mean(returns[r][c]) for c in range(num_col)] \
for r in range(num_row)])
print("average of returns")
print(returns_average)
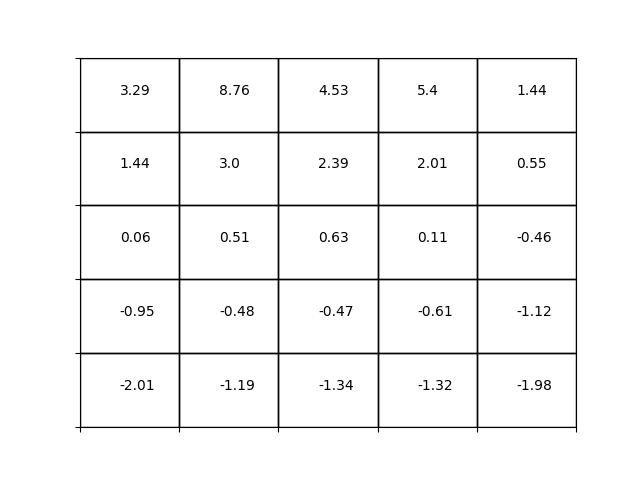
最大ステップは100で終端状態(打ち切り)、モンテカルロ法のサンプリング回数は10000回にしています。各サンプリングでは初期値をランダムに設定して、そこから方策に従ってエピソードを進めていきます。といっても今回の方策も、ランダムに上下左右進めるので、完全なるランダムウォークです。
ランダムウォークによってたどり着く終端状態での報酬はエピソードごとに異なります。その結果を、初期位置ごとに分けたリストに追加(append)していきます。
試行が終わった後は各状態に追加された報酬の平均を取り、価値関数を求めます。
注意点としては、5行5列の空リストを作成するときに二重の内包表記を使っている箇所がありますが、その場合は、変数の指定を後で指定するほうから(つまり、この場合col,rowの順で)指定していきます。こうすることによって、追加したリストを指定するときには前から順に$returns[r][c]$と指定できます。
同じ条件で動的計画法(方策評価)を用いて状態価値関数を以下に示します。
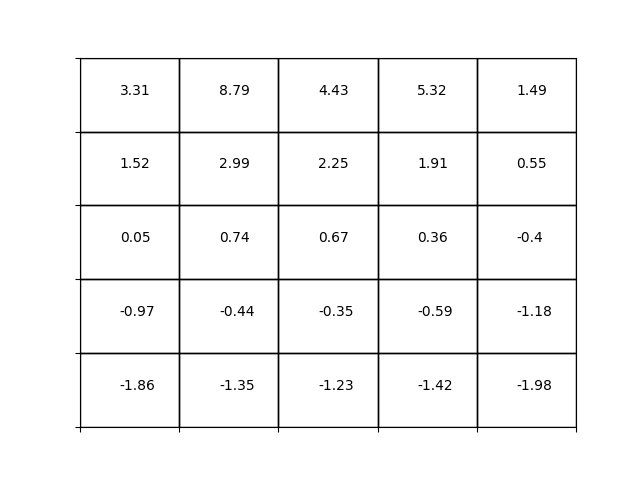
良い一致が見られます。若干違うところもありますが方策を評価するには十分だと思います。
最後に
強化学習でモンテカルロ法を用いて状態価値推定を行いました。次回は行動価値を推定して、最適な行動をとる方策を求めたいと思います。
もういいかげん、グリッドワールドも飽きてきたので次からはOpenAi Gymを使っていきます。こんな風に。見えると楽しい!