はじめに

Adversarial variational Bayes (AVB)を提案した下記の論文にしたがってAVBをPyTorchで実装し、
toy problemできちんとencoderの推定ができるかどうか、試してみました。

Lars Mescheder, Sebastian Nowozin, Andreas Geiger.
Adversarial Variational Bayes: Unifying Variational Autoencoders and Generative Adversarial Networks.
arXiv preprint arXiv:1701.04722, 2017.

2017/11/24の追記

コードのなかのELBOの式が誤っていたので、修正し、実験しなおしました。
もとのコードでは、ELBOの式が

    loglike = torch.mean(- (X - z_sample) * (X - z_sample) / 2.0
                         - (z_sample / prior_scale) * (z_sample / prior_scale) / 2.0)

と、$\log p(z)$を含んだ式になっていました。
しかし、$\log p(z)$の項は、discriminatorの評価値に含まれています。
よって、$\log p(z)$はなしで、

    loglike = torch.mean(- (X - z_sample) * (X - z_sample) / 2.0)

とするのが正しかったです。この修正にともなって、実験結果も差し替えました。
ただし、この記事に関しては、実験結果はあまり代わっていません。
（prior_scaleの値が大きく、間違って追加していた項があまり影響を与えなかったからだと思います。）

Toy problem

観測データを、次のようにして人工的に生成しました。

$\mu_i \sim \mathcal{N}(0, 20)$, for $i=1,\ldots,N$.
$x_i \sim \mathcal{N}(\mu_i, 1)$, for $i=1,\ldots,N$.

注意点を述べておきます。同じ$\mu$を使って$x_i \sim \mathcal{N}(\mu, 1)$としているのではありません。
各観測データについて別々に$\mu_i$を裾野の広い正規分布$\mathcal{N}(0, 20)$からdrawしています。¹

そして、ELBOを以下のように求めます。

\begin{align}
\log \prod_{i=1}^N p(x_i) & = \sum_{i=1}^N \log \int p(x_i | \mu_i)p(\mu_i) d \mu_i \\
& = \sum_{i=1}^N \log \int q(\mu_i | x_i) \frac{p(x_i | \mu_i)p(\mu_i)}{q(\mu_i | x_i)} d \mu_i \\
& \geq \sum_{i=1}^N \int q(\mu_i | x_i) \log \frac{p(x_i | \mu_i)p(\mu_i)}{q(\mu_i | x_i)} d \mu_i
\end{align}

このELBOを少し書き直します（$\sum_{i=1}^N$を$E_{p_{\mathcal{D}(x)}}$に書き直す等）。
すると、ELBO最大化問題は、以下のようになります。

\begin{align}
\max_\theta \max_\phi \mbox{E}_{p_{\mathcal{D}(x)}} \mbox{E}_{q_\phi(\mu_i | x_i)} \big( & \log p(\mu_i) - \log q_\phi(\mu_i | x_i) +  \log p_\theta(x_i | \mu_i) \big)
\end{align}

これは、上掲論文の式(3.1)に対応します。
今回の設定では$q_\phi(\mu_i | x_i)$が解析的に分かってしまいますが、あえてDNNを使ってimplicitに表現します。
すると、密度関数の式が書けなくなり、特殊な推定方法が必要になるわけですが、詳細は上掲論文をご覧ください。

コード

それほど長くないので、下に示します。

simple_avb.py

import torch
import torch.nn
import torch.nn.functional as nn
import torch.autograd as autograd
import torch.optim as optim
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
import os

torch.manual_seed(123)
np.random.seed(123)

mb_size = 100
z_dim = 1
eps_dim = 2
X_dim = 1
h_dim = 8
cnt = 0
lr = 0.00001

def log(x):
    return torch.log(x + 1e-8)

# Encoder: q(z|x,eps)
Q = torch.nn.Sequential(
    torch.nn.Linear(X_dim + eps_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, z_dim)
)

for l in Q:
    if type(l) == torch.nn.ReLU:
        torch.nn.init.xavier_normal(prev_l.weight)
    prev_l = l

# Discriminator: T(X, z)
T = torch.nn.Sequential(
    torch.nn.Linear(X_dim + z_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, 1)
)

for l in T:
    if type(l) == torch.nn.ReLU:
        torch.nn.init.xavier_normal(prev_l.weight)
    prev_l = l

def reset_grad():
    Q.zero_grad()
    T.zero_grad()

prior_scale = 20.0 

def sample_prior(size):
    return np.random.normal(loc=0.0, scale=prior_scale, size=size)

def sample_X(size):
    mu = sample_prior(size)
    X = np.random.normal(loc=mu, scale=1.0).astype(np.float32)
    X = Variable(torch.from_numpy(X))
    return X

Q_solver = optim.Adam(Q.parameters(), lr=lr)
T_solver = optim.Adam(T.parameters(), lr=lr)

for it in range(1000000):
    X = sample_X((mb_size, 1))
    eps = Variable(torch.randn(mb_size, eps_dim))

    z = sample_prior((mb_size, z_dim))
    z = Variable(torch.from_numpy(z.astype(np.float32)))

    # Optimize VAE
    z_sample = Q(torch.cat([X, eps], 1))
    T_sample = T(torch.cat([X, z_sample], 1))

    disc = torch.mean(-T_sample)
    loglike = torch.mean(- (X - z_sample) * (X - z_sample) / 2.0) # modified on 2017/11/24

    elbo = - (disc + loglike)

    elbo.backward()
    Q_solver.step()
    reset_grad()

    # Discriminator T(X, z)
    z_sample = Q(torch.cat([X, eps], 1))
    T_q = nn.sigmoid(T(torch.cat([X, z_sample], 1)))
    T_prior = nn.sigmoid(T(torch.cat([X, z], 1)))

    T_loss = - torch.mean(log(T_q) + log(1.0 - T_prior))

    T_loss.backward()
    T_solver.step()
    reset_grad()

    # Print and plot every now and then
    if it % 10000 == 0:
        print('Iter-{}; ELBO: {:.4}; T_loss: {:.4}'
              .format(it, -elbo.data[0], -T_loss.data[0]))

        X = Variable(torch.ones(1000, 1)* (- 3.0))
        eps = Variable(torch.randn(1000, eps_dim))
        z_sample = Q(torch.cat([X, eps], 1))
        z_sample = z_sample.squeeze().data.numpy()
        n, bins, patches = plt.hist(z_sample, 50)

        X = Variable(torch.ones(1000, 1) * 10.0)
        eps = Variable(torch.randn(1000, eps_dim))
        z_sample = Q(torch.cat([X, eps], 1))
        z_sample = z_sample.squeeze().data.numpy()
        n, bins, patches = plt.hist(z_sample, 50)

        plt.xlim(-6, 14)
        plt.ylim(0, 60)

        if not os.path.exists('out/'):
            os.makedirs('out/')

        plt.savefig('out/{}.png'
                    .format(str(cnt).zfill(4)), bbox_inches='tight')
        plt.clf()

        cnt += 1

このコードは、下記の場所にあるものを参考にしました。

Collection of generative models, e.g. GAN, VAE in Pytorch and Tensorflow.

今回は、decoderである$p(x_i | \mu_i)$がそれ自身のパラメータを持っていないので、コードの中には現れていません。
しかし、$p(x_i | \mu_i)$の対数をとったものは、loglikeを設定している行に現われています。

(2017/11/01の追記: 活性化関数がReLUなのに、なぜかxavierを使ってましたね（汗）。kaimingのほうが良かったかもしれません。)

2017/11/24の追記:
上で述べたように、コードのなかのELBOの式が間違っていました。誤って、$\log p(z)$の項を書いていました。
この項は、discriminatorの評価値に含まれる値であるため、$\log p(z)$の項が書いてあるのは間違いでした。
下の実行結果も、差し替えてあります。

実行結果

実行結果を見る前に、正解が何かを述べておきます。

\begin{align}
p(\mu_i | x_i) & \propto p(x_i | \mu_i) p(\mu_i) \\
& \propto \exp \bigg( - \frac{ (x_i - \mu_i)^2 }{ 2 } \bigg) \times \exp \bigg( - \frac{ \mu_i^2 }{ 800 } \bigg) \\
& \propto \exp \bigg( - \frac{ (\mu_i - x_i)^2 }{ 2 } - \frac{ \mu_i^2 }{ 800 } \bigg)
\end{align}

$\frac{ \mu_i^2 }{ 800 }$の部分は、正確に言えば無視できませんが、かなり小さいです。
（2017/11/20の追記：分母が$400$になっていたのを、$2 \times 20^2 = 800$に修正しました。）
ということは、おおよそで言えば、$\mu_i$は$x_i$を中心として標準偏差1ぐらいで散らばっている正規分布に従うはずです。
今回推定されたencoder $q_\phi(\mu | x)$も、入力$x$を中心として標準偏差1ぐらいで散らばる出力を与えてくれるはずです。

では、上のコードが作成したヒストグラムを示します。
コードでは、encoderの入力として$x=-3$とした場合（青色）と、$x=10$とした場合（オレンジ色）について、
それぞれランダムな入力（論文でいう$\epsilon_1$）を1000回与えてヒストグラムを描いています。

ヒストグラムは、学習が進むにつれて、少しずつ変化しました。

まず、最初のミニバッチだけを見た後です。ミニバッチのサイズは100です。

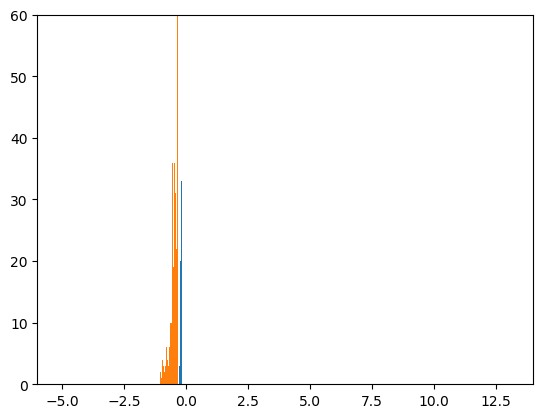
全然ダメです（笑）。
次に、10,000個のミニバッチを見た後です。

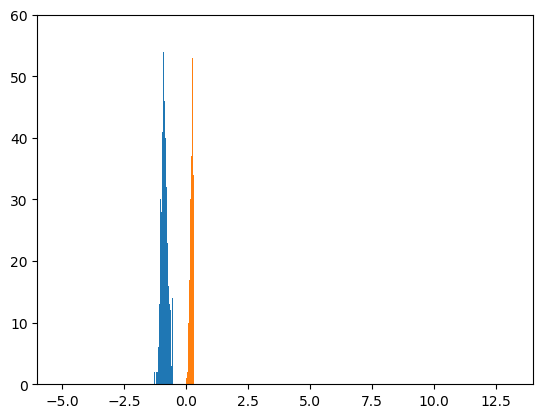
$x=-3$とした場合（青色）と、$x=10$とした場合（オレンジ色）が、すこし離れてきました。
20,000個のミニバッチを見た後と、30,000個のミニバッチを見た後を、続けて示します。

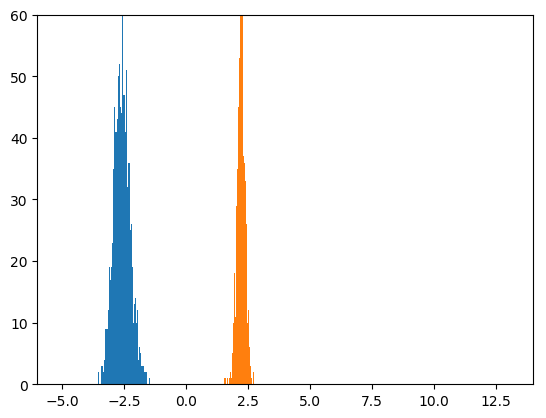
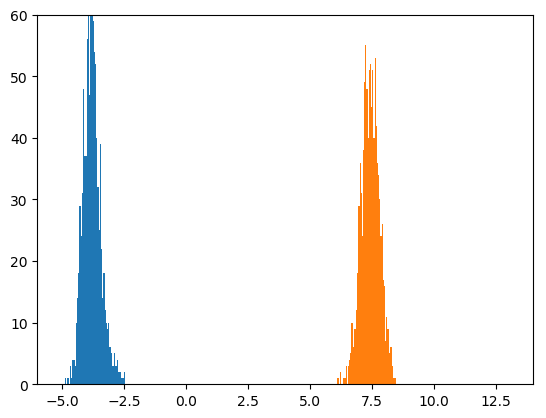
良くなってきました。
200,000個のミニバッチを見た後は、次のようになります。

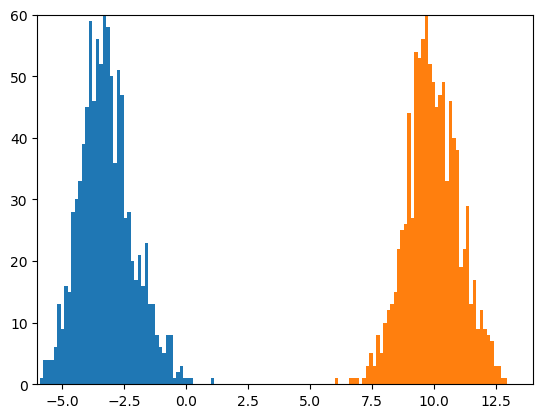
これはきれいな感じに見えます。
しかし、このまま動かし続けると、800,000個のミニバッチを見た後は、こうなります。

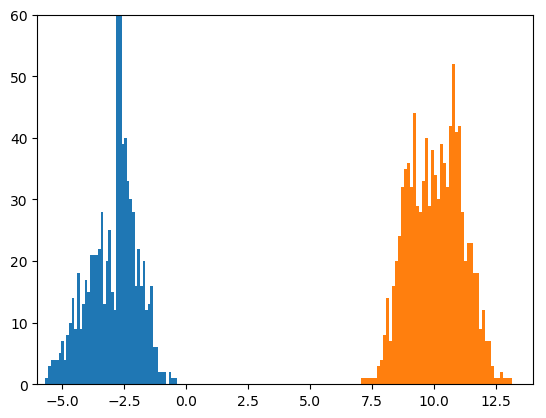
$x=-3$のほうが大きく崩れています。早めに止めたほうがいいのかもしれません。

最後に、ミニバッチを1,000,000個見るまでのELBOの変化と、論文の式(3.3)に相当する値（コードのなかの-T_loss）の変化を、
グラフで示しておきます。

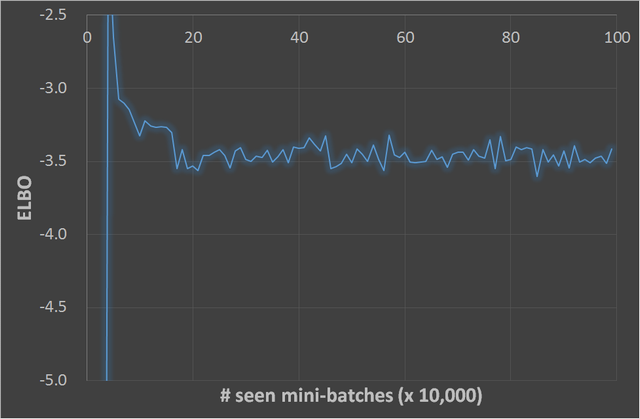
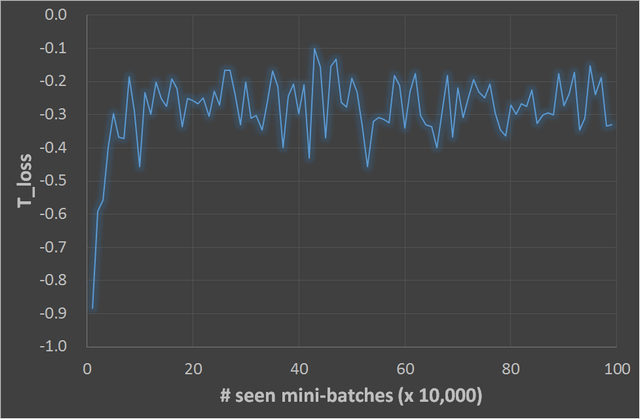
まとめ

今回は、toy problemでadversarial variational Bayesを試してみました。
VAEは使ったことはありますが、encoderの選択に制約があるのが気になっていました。
現実的な問題についてもencoderをimplicitな分布にしてみようかなという勇気（？）が湧いてきました。

2017/11/2 追記（2017/11/24の修正をふまえて図は差し替え）

重みの初期化を変えると、結果がどう変わるか、調べてみました。
上のコードで作られる途中経過のヒストグラムを100個、ひとつの図にまとめました。
最初のヒストグラムは左上隅で、mini-batchを1つだけ見た後。
最後のヒストグラムは右下隅で、mini-batchを990,001個見た後です。

まず、上のコードどおりの場合。つまり、encoderもdiscriminatorもxavier_normalで初期化した場合。

次に、同じxavierでもxaivier_uniformにした場合。

uniformのほうが良かったかもしれません。
では、kaiming_normalで初期化した場合。

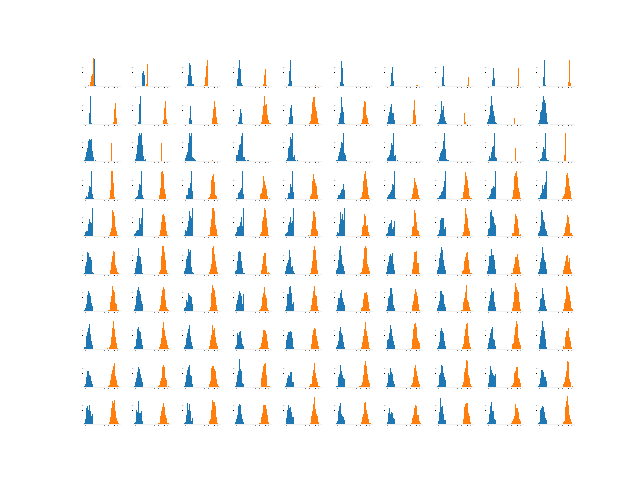
（2017/11/24修正）~~$x=10$のほうがなぜか全くうまくいきません。~~
同じkaimingでもkaiming_uniformにすると、下のようになりました。

（2017/11/24修正）~~こちらのほうが良いように見えます。~~
以上、追記でした。