Adversarial variational Bayesをtoy problemで試す（続編）

はじめに

今回は、少し前に投稿したAdversarial variational Bayes (AVB)に関する記事の続編です。

2017/11/24の追記:
これは続編ですが、前回の記事に修正が入ったため、こちらのほうも修正しています。
修正の内容については、以下の本文中で述べています。

AVBは、変分近似分布にimplicitな分布を使っていても、ELBOの最大化ができるようにする手法です。
特徴は、対数密度比のestimationを、GANと同様な方法で実現していることです。

なお、AVB含め、implicitな分布を使う場合の変分推定についてまとめて議論している論文がありました。

• Ferenc Huszár. Variational Inference using Implicit Distributions. arXiv:1702.08235

この論文で言うと、AVBはAlgorithm 1に相当します。

前回との違い

さて、続編ですので、前回の記事に改良を加えます。

推定するパラメータを増やす

2017/11/24の追記：
ここに書いてあった内容は、技術的に誤っていることが分かりましたので、削除しました。
前回の記事について修正をおこなったように、ELBOの式に$\log p(z)$に対応する項が書かれていましたが、
これはDiscriminatorの値に含まれていますので、$\log p(z)$を書いていたのは誤りでした。
したがって、$p(z)$に未知のパラメータをもたせてその値を推定するということは、AVBでは不可能です。
（AVBの枠外で別に考えることはできます。上掲論文のAlgorithm 1の下に位置する段落に書いてあります。）
この意味で、ここに書いてあった内容は誤りでした。

変分近似分布の推定の学習率を大きくする

前回は、とてもたくさんのサンプルを使って訓練していましたが、これは単に学習率が小さかっただけでした（汗）。
Adamの学習率を10倍にし、0.0001としました。これ以上増やすと、良くないようです。

Discriminatorの最適化を複数回にする

前回は、Discriminatorの最適化と、変分近似分布$q(\mu_i | x_i)$の最適化とを、1回ずつ交互におこなっていました。

今回は、Discriminatorの最適化を5回繰り返してから、$q(\mu_i | x_i)$の最適化を1回実行します。
上掲論文で言えば、Algorithm 1で$K=5$とした場合に相当します。

2017/11/24の追記: $\log p(z)$に関する修正をおこなった後では、$K=5$とするのでは、結果が悪くなりました。
そこで、下に示す実装では、$K=1$に戻してあります。

Discriminatorの最適化をSGDにする

前回はAdamでしたが、DiscriminatorのほうはSGDでも良さそうだったので、SGDにしました。
学習率は0.01ぐらいが良いようです。

実装

以下の通りです。
上で述べた以外の細かい変更も加えています。

simple_avb_2.py

import torch
import torch.nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
import os

torch.manual_seed(123)
np.random.seed(123)

mb_size = 100
z_dim = 1
eps_dim = 2
X_dim = 1
h_dim = 8
cnt = 0
lr = 0.0001
sgd_lr = 0.01

def log(x):
    return torch.log(x + 1e-10)

# Encoder: q(z|x,eps)
Q = torch.nn.Sequential(
    torch.nn.Linear(X_dim + eps_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, z_dim)
)

for l in Q:
    if type(l) == torch.nn.ReLU:
        torch.nn.init.xavier_normal(prev_l.weight)
    prev_l = l

# Discriminator: T(X, z)
T = torch.nn.Sequential(
    torch.nn.Linear(X_dim + z_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, h_dim),
    torch.nn.ReLU(),
    torch.nn.Linear(h_dim, 1)
)

for l in T:
    if type(l) == torch.nn.ReLU:
        torch.nn.init.xavier_normal(prev_l.weight)
    prev_l = l

def reset_grad():
    Q.zero_grad()
    T.zero_grad()

true_scale = 20.0
def sample_X(size):
    mu = np.random.normal(loc=0.0, scale=true_scale, size=size)
    X = np.random.normal(loc=mu, scale=1.0).astype(np.float32)
    X = Variable(torch.from_numpy(X))
    return X

Q_solver = optim.Adam(list(Q.parameters()), lr=lr)
T_solver = optim.SGD(T.parameters(), lr=sgd_lr, momentum=0.9)

for it in range(100000):

    # Discriminator
    for _ in range(1):
        X = sample_X((mb_size, 1))
        eps = Variable(torch.randn(mb_size, eps_dim))
        z = Variable(torch.randn(mb_size, z_dim) * true_scale)

        z_sample = Q(torch.cat([X, eps], 1))
        T_q = F.sigmoid(T(torch.cat([X, z_sample], 1)))
        T_prior = F.sigmoid(T(torch.cat([X, z], 1)))

        T_loss = - torch.mean(log(T_q) + log(1.0 - T_prior))

        T_loss.backward()
        T_solver.step()
        reset_grad()

    # Encoder
    X = sample_X((mb_size, 1))
    eps = Variable(torch.randn(mb_size, eps_dim))

    z_sample = Q(torch.cat([X, eps], 1))
    T_sample = T(torch.cat([X, z_sample], 1))

    disc = torch.mean(-T_sample)
    loglike = torch.mean(- (X - z_sample) * (X - z_sample) / 2.0)

    elbo = - (disc + loglike)

    elbo.backward()
    Q_solver.step()
    reset_grad()

    # Print and plot every now and then
    if it % 1000 == 0:
        print('Iter-{}; ELBO: {:.4}; T_loss: {:.4}'
              .format(it, -elbo.data[0], -T_loss.data[0]))

        X = Variable(torch.ones(1000, 1) * - 3.0)
        eps = Variable(torch.randn(1000, eps_dim))
        z_sample = Q(torch.cat([X, eps], 1))
        z_sample = z_sample.squeeze().data.numpy()
        n, bins, patches = plt.hist(z_sample, 50)

        X = Variable(torch.ones(1000, 1) * 10.0)
        eps = Variable(torch.randn(1000, eps_dim))
        z_sample = Q(torch.cat([X, eps], 1))
        z_sample = z_sample.squeeze().data.numpy()
        n, bins, patches = plt.hist(z_sample, 50)

        plt.xlim(-8, 15)
        plt.ylim(0, 80)

        if not os.path.exists('out/'):
            os.makedirs('out/')

        plt.savefig('out/xnxn_00_{}.png'.format(str(cnt).zfill(4)), bbox_inches='tight')
        plt.clf()

        cnt += 1

実験結果

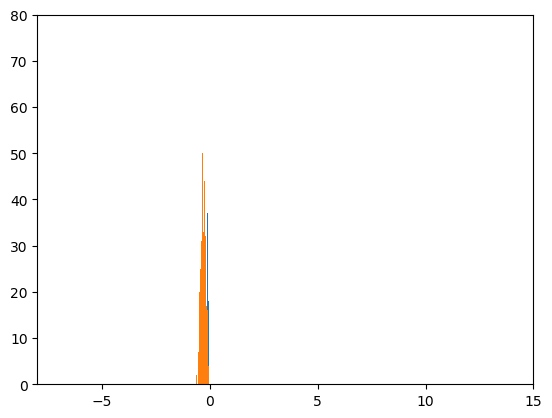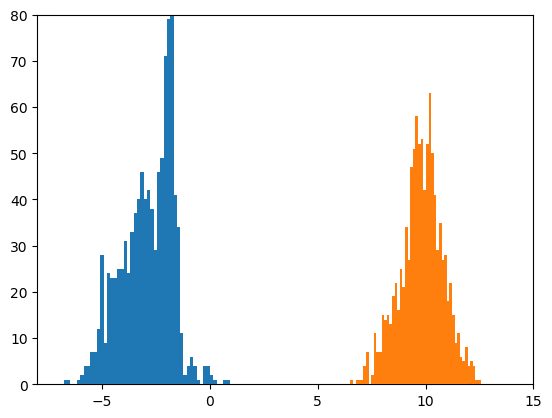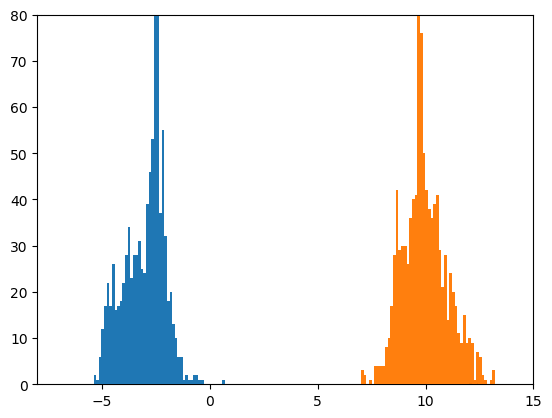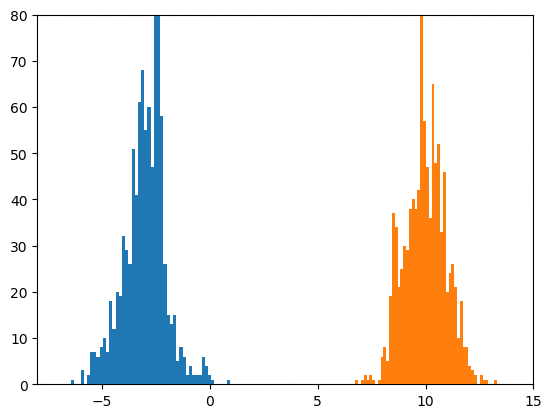
サイズ100のミニバッチを1000個見るごとに、前回と同様なヒストグラムを作成しました。
おおよそ-3と10の位置を平均とし、だいたい標準偏差が1になっている二つの正規分布が見えれば、
うまくいっていることになります。

100枚の画像をanimated gifにしたものを示します。
2017/11/24の追記: 上記の修正にともなって、xavier_normalによる初期化の場合の結果に差し替えています。

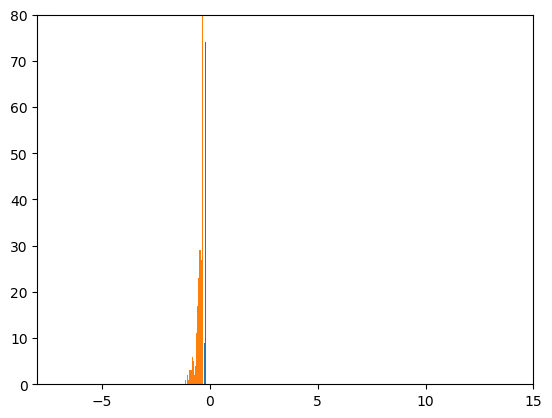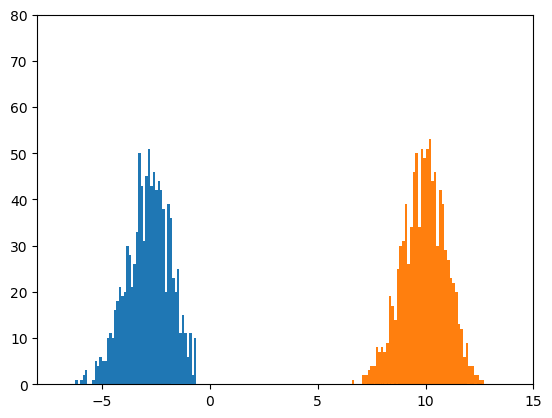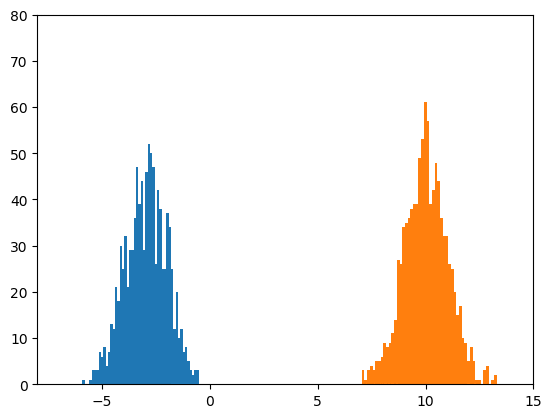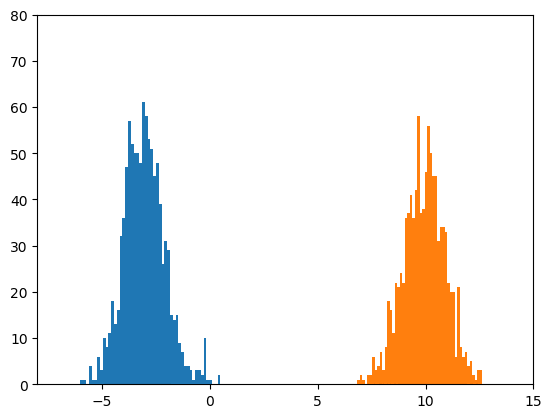
2017/11/24の追記: 参考までに、xavier_uniformによる初期化の場合の結果も示します。
どちらのヒストグラムも形がくずれており、あまり良くありません。

まとめ

Adversarialな方法に慣れてきた気もしないでもありません。
いずれは自分の研究で使ってみたいと思います。

2017/11/24の追記:
すでに述べたように、前回の記事とこの記事とで、同じ間違いを見つけて修正しました。
これは、引き続きAVBを別のケースで使ってみようと試行錯誤していて、発見した間違いです。
やはり、同じ手法でも、いろいろなケースで試してみようとすることは大事なようです。