公開？週末研究ノート ー 関数ベクトル空間②（検証編）

はじめに　ー　週末研究ノートとは？

個人的に研究的な活動をやるにあたり、オープンにしてみたら面白いかもと思い、自分が興味を持っている ざっくりテーマについて、これから、ゆるい週末研究を公開していこうと思います。（有識者の方のアドバイスも、ちょっとというかかなり期待してます！笑）

どこかの権威的な学会やジャーナルなどで発表する予定はないため、万が一、私の記事を利用する際には自己責任でお願いします。そんな人はいないと思いますが、念のため。

今回のサマリ （TL; DR）

今回は、関数ベクトル空間の基底として有名な $\{ \cos(kx), \sin(kx) \}_{k \in \mathbb{N}}$ を可視化してみます。

今回の可視化の前提となる理論的な背景は、公開！週末研究ノート０２　ー　関数ベクトル空間①（理論編）を参照されたい。

環境

• Google Colaboratory
  • コードは、こちら

今回の週末研究ノート

関数ベクトル空間上の基底の定義

データ化

$\sin kx, \cos kx$ をベクトル化したデータをDataFrame　として返す関数を作成しておく

import numpy
import pandas
from matplotlib import pyplot

def make_base_function_kx(K: int, N: int, basis_f: numpy.ufunc=numpy.cos) -> numpy.ndarray:
    interval = numpy.arange(-1.0, 1.0+2/N, 2/N)
    x = interval * numpy.pi
    f_kx = basis_f(x)

    for k in range(2, K+1):
        f_kx = numpy.vstack((f_kx, basis_f(k*x)))

    df = pandas.DataFrame(f_kx)
    df.index = [f"{basis_f.__name__}{k}x" for k in range(1, K+1)]
    df.columns = [f"{unit:0.2f}π" for unit in interval]
    return df

作った関数でベクトル化データを作成

K= 200  # max vector basises, i.e. dim of basis_f
N = 300   # grid for x, dim x = N + 1

cos_kx = make_base_function_kx(K, N, basis_f=numpy.cos)
sin_kx = make_base_function_kx(K, N, basis_f=numpy.sin)
basis_kx = pandas.concat([cos_kx, sin_kx], axis=0)

cos_labels = numpy.array((["cos"] * K))
sin_labels = numpy.array((["sin"] * K))
basis_labels = numpy.concatenate([cos_labels, sin_labels], axis=0)

出力は、こんな感じ

cos_kx.head()

作った関数ベクトルを可視化

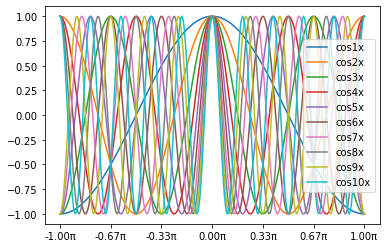
• $\cos kx$

cos_kx[:10].transpose().plot()
pyplot.show()

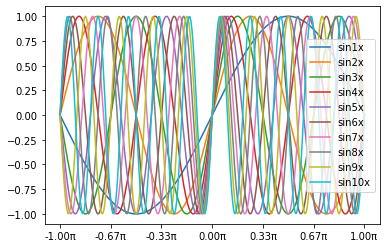
• $\sin kx$

sin_kx[:10].transpose().plot()
pyplot.show()

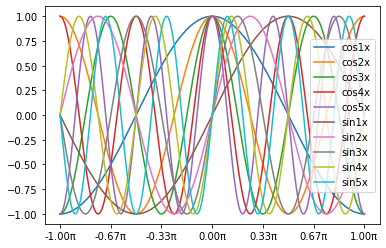
• $\cos kx, \sin kx$

basis_samples = pandas.concat([cos_kx[:5], sin_kx[:5]], axis=0)
basis_samples.transpose().plot()
pyplot.show()

関数ベクトル空間上の基底の可視化

では、お待ちかね？！の基底を可視化してみます。

2D, 3D 用のプロット関数を定義しておきます。

import seaborn as sns
import plotly.express as px
import plotly.graph_objects as go

def plot_3D(x, y, z, labels):
    fig = go.Figure(data=[go.Scatter3d(
        x=x,
        y=y,
        z=z,
        text=data.index,
        mode='markers+text',
        marker=dict(
            size=3,
            color=["pink" if l == "cos" else "skyblue" for l in labels],
            colorscale='Viridis',   # choose a colorscale
            opacity=0.7
        )
    )])

    # tight layout
    fig.update_layout(margin=dict(l=0, r=0, b=0, t=0))
    fig.show()

def plot_2D(X: numpy.ndarray, names: list, offset=0.25):
    df = pandas.DataFrame(X, columns=["PC1", "PC2"])
    df["names"] = names
    # fig = px.scatter(df, x="PC1", y="PC2", text="names")
    fig = go.Figure(data=[go.Scatter(
        x=df.PC1,
        y=df.PC2,
        text=df.names,
        mode='markers+text',
        marker=dict(
            size=8,
            color=["pink" if l == "cos" else "skyblue" for l in labels],
        )
    )])
    fig.update_layout(margin=dict(l=0, r=0, b=0, t=0))
    fig.show()

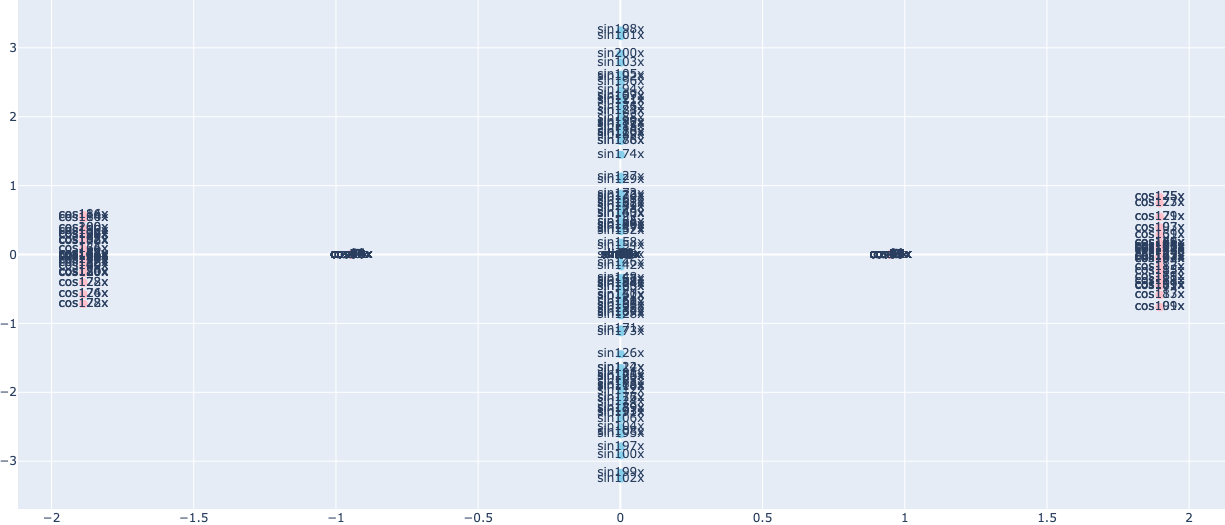
• PCA で可視化

まずは、オーソドックスな PCA　で 2次元に射影したデータを使って可視化してみます。

from sklearn.decomposition import PCA
X = PCA(n_components=2).fit_transform(data)
plot_2D(X, names=data.index)

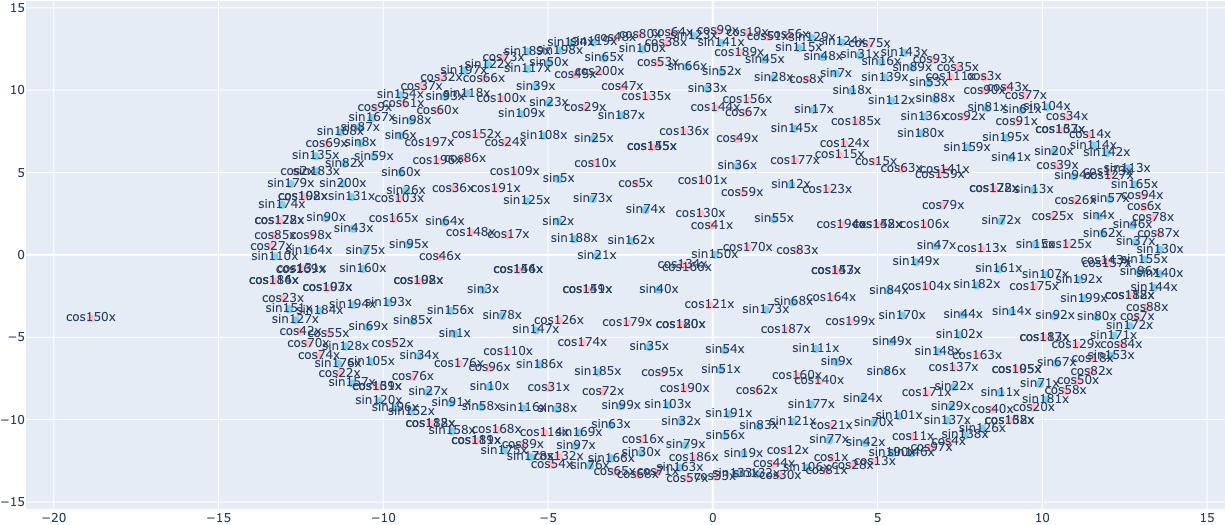
$\sin kx$ と $\cos kx$ で大きく５つの分かれているように見えます。
$\sin kx$ が 第２軸に集中して分布しているように見えます。
一方、 $\cos kx$ は、４つの領域に線対称に分布しているように見えます。

• MDS で可視化

from sklearn.manifold import MDS
model = MDS(n_components=2)
X = model.fit_transform(data)
plot_2D(X, names=data.index)

MDS では、$\sin kx, \cos kx$ が、円状に分布しているように見えます。

• UMAP

import umap
import umap.plot

mapper = umap.UMAP().fit(data)
umap.plot.points(mapper, labels=labels, color_key_cmap='Paired')
pyplot.show()

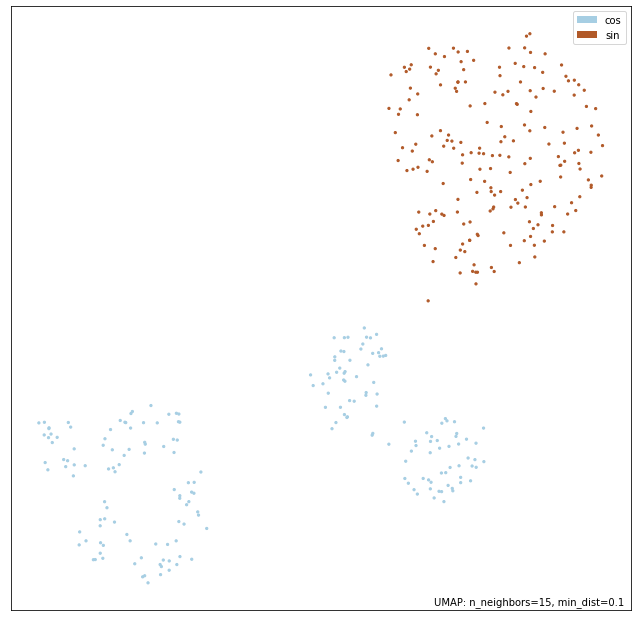
UMAP では、PCA のように $\sin kx$ と $\cos kx$ で 大きく５つに分布しているように見えます。
特に、 $\sin kx$ は １つの大きなクラスタとしてまとまっているように見えます。

• UMAP (connectivity)

近傍のエッジを表示してみる

umap.plot.connectivity(mapper, show_points=True)
pyplot.show()

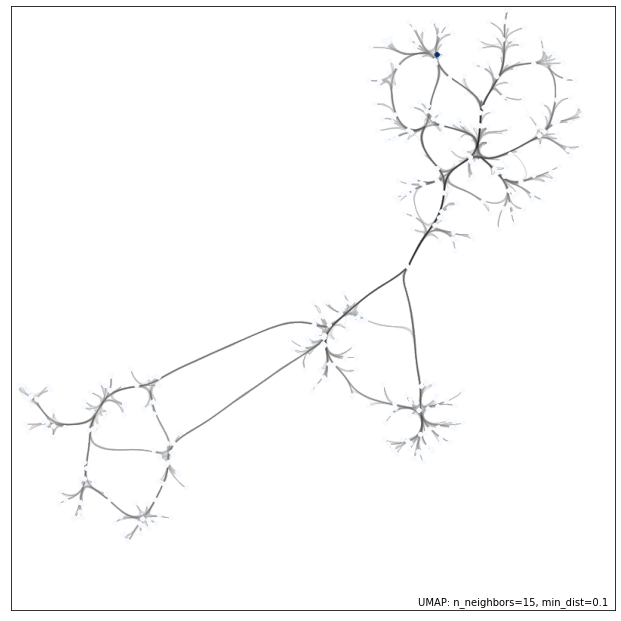
中央あたり（おそらく ０ ベクトル）から、右上方向に $\sin kx$ 左下方向に $\cos kx$ が広がるように分布しているように見えます。

• UMAP (connectivity - hammer)

連結が多い（重なる）部分を濃く表示する edge_bundling で表示してみます。（この解釈合ってるかな？？）

umap.plot.connectivity(mapper, show_points=True, edge_bundling='hammer')
pyplot.show()

$\sin kx, \cos kx$ の基底をノードとする木構造で可視化すると、なんとなく、脳に近い印象を受けますね。

• UMAP (local_dim)

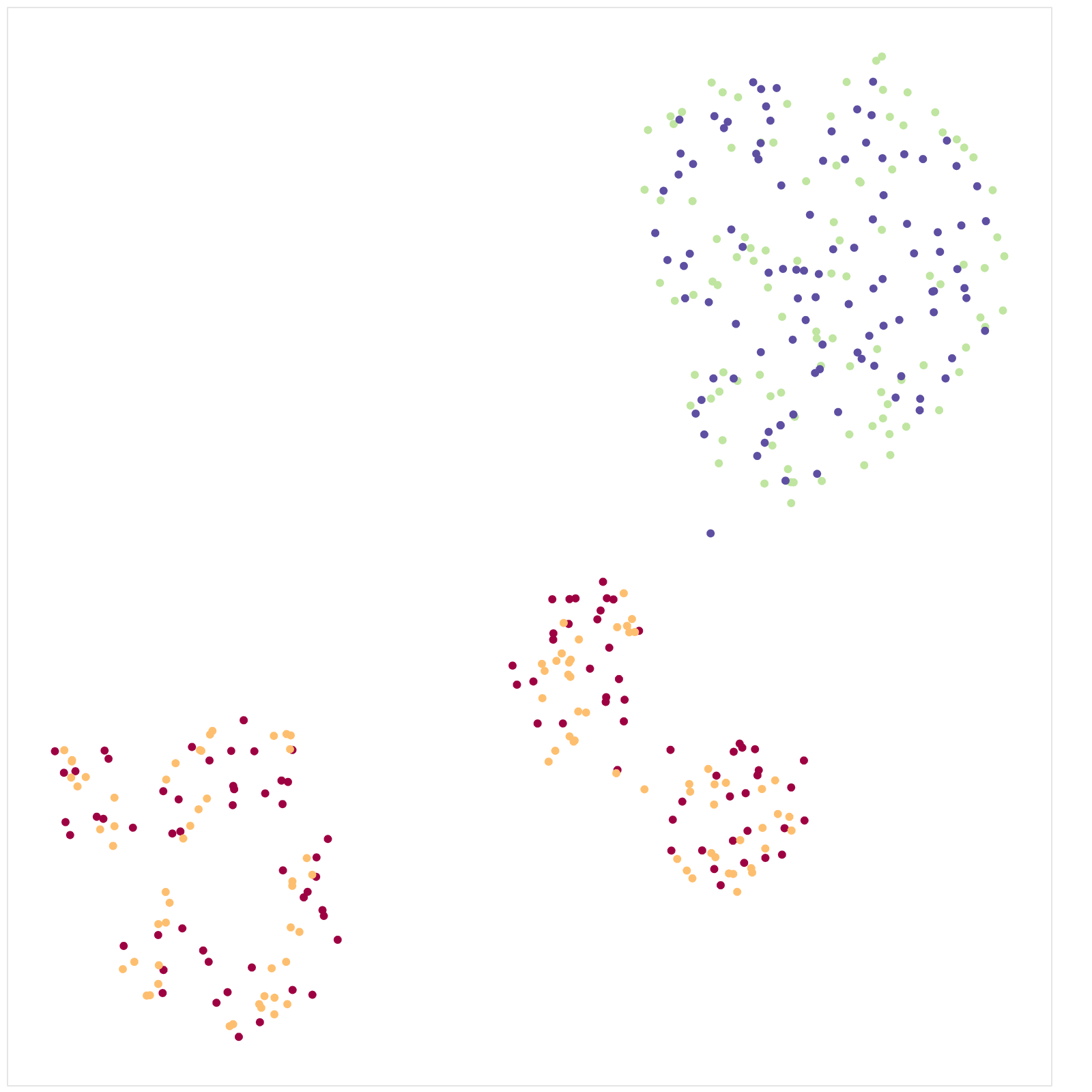
局所次元をカラー表示してみます。

umap.plot.diagnostic(mapper, diagnostic_type='local_dim')
pyplot.show()

$\cos kx$ の 5〜8次元ぐらいと比べると、$\sin kx$ の10 次元が高次元上に分布しているように見えます。

• UMAP をノートブックでぐりぐり動かす

umap.plot.output_notebook()

n_digits = int(numpy.log10(len(data)))
index_labels = numpy.arange(len(data)) // (10 ** n_digits)
df_text = data.reset_index()[["index"]]
p = umap.plot.interactive(mapper, labels=index_labels, hover_data=df_text, point_size=5)
umap.plot.show(p)

↓のように表示され、マウスでぐりぐりできます。

まとめ

• 関数ベクトル空間の基底である $\sin kx, \cos kx$ を可視化してみた
  • PCA, MDS, UMAP を使って可視化
  • それぞれが、それぞれの視点による可視化であるので、いずれも矛盾しない解釈をしたいところ
  • PCA, UMAP から 大きく 5つのクラスタに分かれるように見える
    • 見方によっては、PCA　のように 十字型に分布されたり、UMAP のように 多角推？円錐？のように分布される様子
    • edge_bundle を使って木構造で表現すると、脳のような分布にも見えなくはない
  • MDS　では、円状・楕円状に分布しているように見える
  • なんとなくだが、部分部分が円や円錐になるフラクタル構造ができているような印象を受けた
• その他、ノートブックでは、上記以外にも可視化していますので、ご参考ください
  • 球面多様体上にマップして可視化
  • フーリエ級数展開（$\sin kx, \cos kx$）による関数の近似とその可視化

参考文献

• Pythonで多次元尺度法 (MDS) 〜距離行列から位置関係を再現する〜
• UMAP 0.4の新機能で遊ぶ（プロット、非ユークリッド空間への埋め込み、逆変換）
• Plotting UMAP results
• Text and Annotations in Python
  
• HIERARCHICAL EDGE BUNDLING