はじめに
この記事では「量子アニーリング方式」での最適化問題解決のために、QUBO形式での定式化について理解することを目標としています。
同様の解説記事は一般化していたり、数式をがっつり使っていたりで、かなり敷居の高いものが多いと感じるため、
量子アニーリング利用のはじめの一歩として読んでもらえる内容を目指しています。
QUBO形式での立式を理解するための解説であり、実機(量子アニーリングマシン等)を利用するためのプログラムの解説はしていません
導入
量子アニーリングとは
アニーリング
そもそも「アニーリング(焼きなまし)」は材料工学・物理の用語で、金属やガラスなどを高温で加熱し、ゆっくり冷やすことで結晶構造を整える熱処理のこと。
高温にして全体の状態を均一化
→ ゆっくり冷やすことで、全体が均一なまま安定
→ 「全体として」最も安定した(最適な)状態になる
というイメージ。
量子アニーリング
「量子ゆらぎ」(量子トンネル効果)を使って、最も安定した状態を見つける。
量子ゆらぎでエネルギーの山を透過(トンネル)することで、より安定なエネルギーの低い状態を探索する。
どんな問題が得意か
最小エネルギーを求める手法であり、最適化問題が得意。
具体例としては、巡回セールスマン問題(TSP)、グラフ彩色、スケジューリングなど。
なぜ量子アニーリング方式を使うのか
量子コンピュータをつくりたいが、汎用的な量子ゲート方式は大規模化や誤り訂正が難しい
→ 量子アニーリング方式は、現実に動かせる量子計算機として早期から提供されてきた
→ 量子技術の実証や応用事例として使いやすい
量子アニーリング方式で最適化問題を解く流れ
- 現実の問題を0と1の組み合わせで再定義
- ルール(制約)をQUBO形式で定式化
- コーディング(Python)
- 量子アニーリングマシンで実行
- 解を得る
今回は 1 と 2 の考え方を理解することが目的。
QUBO形式でのルール定式化は、Pythonを使ったコーディングをしながら進める。
定式化(QUBO式)
QUBOとは
ここは専門用語や数式が多めなので興味ない方は流してください
D-Wave System社などの量子アニーリングマシンでは、解きたい課題をイジングモデルやQUBO形式に対応させて扱う。
イジングモデル
物理学でスピン(=磁石の性質)を持つ粒子の集まりを表現するモデル。集まった量子それぞれのスピンが上下どちらを向くか(変な方向は向かない前提)で全体のエネルギーが決まるというルールの上で、エネルギーの最小値を求める
Quadratic Unconstrained Binary Optimization(QUBO)
日本語では「二次の制約なし二値最適化問題」
各単語をみていくと、
- Quadratic:変数の多項式の次数は2次まで(変数の2乗または1次変数同士の積)
- Unconstrained:制約(条件)がない
- Binary:変数は0か1のみ
- Optimization:これらを満たす目的関数(エネルギー)を最小化する
イジングモデルとQUBOの見た目は違うが、本質的には同じ数式で表せる。
配置・割当問題など多くの実用課題に使われる。
制約が必要な場合はペナルティ項を目的関数に加えて表現する。
ただし、全ての最適化問題がQUBOで解けるわけではない。現実の問題の多くのパターンはこの形式に落とし込める(+計算しやすい)ため、量子アニーリング方式に限らずよく使われる。
※より高次も扱うHigh Order Binary Optimization(HOBO)は本記事では触れない。
QUBO形式の目的関数の一般形は以下である。(わからなくてよい)
\min\left(\sum_i Q_{ii} x_i + \sum_{i<j} Q_{ij} x_i x_j\right)
- $x_i \in {0, 1}$:変数
- $Q$:定数の係数行列
大事なことは、変数が0か1しかとらないこと。
選ぶ/選ばないなど0と1で表現できるように、現実の問題をいい感じに再定義する必要がある。
実践
最適化問題として有名な巡回セールスマン問題(TSP)を題材に、QUBO式の立て方を簡単なパターンから順番に説明する。
問題設定
4箇所の町A, B, C, Dがあるとする(線の近くにある数字は距離)
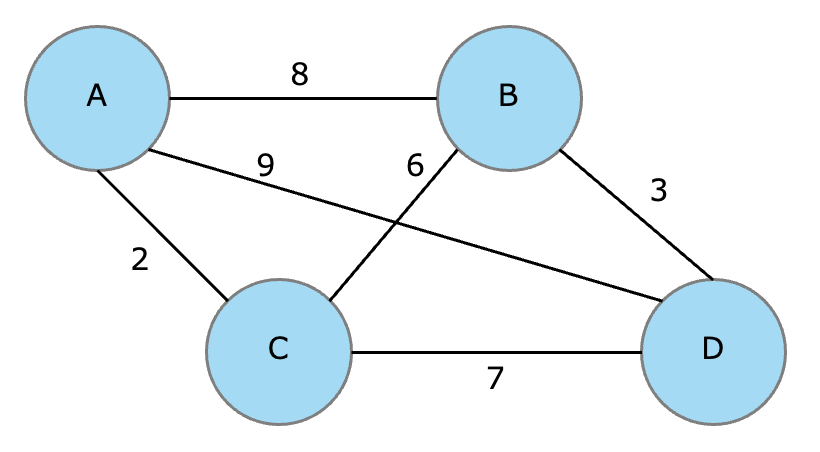
1. 数量の制約
まずA, B, C, Dの4箇所から1つだけ選ぶ場合を考える。
プログラム上ではA, B, C, Dに変数q[0], q[1], q[2], q[3]を割り当てる。
q[i] (i = 0~1) はそれぞれ0か1しか取らないとする(0は選ばない、1は選ぶ)。
このときの目的関数 H は:
H = (q[0] + q[1] + q[2] + q[3] - 1) ** 2
とすればよい。
エネルギーを表す演算子(Hamiltonian)を物理学で$H$と表記するので、目的関数もHとしている。
このように、複数の変数に対して、1つだけ「1」、他の変数を「0」とする制約のことをOne-hot エンコーディングと呼ぶ。
実際に数値を入れて計算してみると、
| 選んだ数 | Hの値 | 具体例 |
|---|---|---|
| 0 | 1 | q[i] は全て 0 |
| 1 | 0 | q[i] のいずれか1つが 1 |
| 2 | 1 | |
| 3 | 4 | |
| 4 | 9 | q[i] は全て 1 |
→ 1箇所だけ選んだときが最小エネルギーとなる
この「1つだけ選ぶ」条件を満たす数式は他にもいろいろ考えられるが、大事なのは「最小値がちょうど1箇所選択の時にだけ出る」こと。
2. 隣接の制約
次はA, B, C, Dの4箇所から2つ選ぶ。
ただし、選ぶ2つは隣り合った町(四角形の対角の位置にない町)とする
→ A-B、B-C、C-D、D-A はOK、A-D, B-C はダメ
まず「2つだけ選ぶ」制約によって目的関数 H1を考えると、1. 数量制約でやったように、
H1 = (q[0] + q[1] + q[2] + q[3] - 2) ** 2
ここから「隣り合っていない町の組み合わせを避ける」ペナルティ項を加える。
ペナルティ項と書いたが、考え方は2つあり、
(1) 隣り合った時に、エネルギーを低くする
(2) 隣り合わない時に、エネルギーを高くする
のどちらかを導入すればよい。
隣り合う・隣り合わないを数式で表現するには、変数同士をかけたものを考える。
(1)で考えると、コスト関数H2は
H2 = - ( q[0]*q[1] + q[1]*q[2] + q[2]*q[3] + q[3]*q[0] )
(2)で考えると、コスト関数H2は
H2 = + ( q[0]*q[2] + q[1]*q[3] )
と書ける。
今回は(2)で考えた方の項数が少なくて済むので(2)を採用する。
H1の条件(2つだけ選ぶ)を課した上で、H2に具体的な数字を当てはめてみると、
| パターン | H2の値 | 具体例 |
|---|---|---|
| 隣り合う | 0 | q[0] = q[1] = 1 かつ q[2] = q[3] = 0 など |
| 隣り合わない | 1 | q[0] = q[2] = 1 または q[1] = q[3] = 1 |
→ エネルギーを最小とするために、隣り合うような状態をとるはず
最終的な目的関数Hは、H1とH2を足し合わせて
H = (q[0] + q[1] + q[2] + q[3] - 2)**2 + ( q[0]*q[2] + q[1]*q[3] )
となる。最小値は0。
3. 巡回の制約
次は各町を1回ずつ巡回することを考える。
この場合、単純に各町に01をつけても順番を表すことはできないので、4×4行列で町と順番を表す。具体的に、行は各町の番号、列は順番を表すとすれば、q[i][j] は 0 or 1 ($0\leqq$ i, j$\leqq 4$) として巡回のパターンを表すことができる。
例えば、
\begin{pmatrix}
0 & 0 & 1 & 0
\\
1 & 0 & 0 & 0
\\
0 & 0 & 0 & 1
\\
0 & 1 & 0 & 0
\end{pmatrix}
を上の行から見ていくと、Aが3番目、Bが1番目、Cが4番目、Bが2番目となるため、この行列は「B → D → A → C」 の順番に回ることを表している。
まず行に注目すると、各町を1箇所ずつ回るので「1」は1つしかでてこないはずである。そのため1箇所ずつ回るための目的関数H1は、1.個数制約と同様に考えて、
H1 = (q[0][0] + q[0][1] + q[0][2] + q[0][3] - 1) ** 2 + \
(q[1][0] + q[1][1] + q[1][2] + q[1][3] - 1) ** 2 + \
(q[2][0] + q[2][1] + q[2][2] + q[2][3] - 1) ** 2 + \
(q[3][0] + q[3][1] + q[3][2] + q[3][3] - 1) ** 2
この書き方は面倒なので、forループ使って
H1 = 0
for i in range(3):
H1 += (q[i][0] + q[i][1] + q[i][2] + q[i][3] - 1) ** 2
次に列に注目すると、順番が同じ数字になることはないので「1」は1つしかでてこない。順番を決めるための目的関数H2は、
H2 = 0
for j in range(3):
H2 += (q[0][j] + q[1][j] + q[2][j] + q[3][j] - 1) ** 2
最終的な目的関数Hは、H=H1+H2 を足し合わせて、少しまとめると、
H = 0
for i in range(3):
H += (q[i][0] + q[i][1] + q[i][2] + q[i][3] - 1) ** 2
for j in range(3):
H += (q[0][j] + q[1][j] + q[2][j] + q[3][j] - 1) ** 2
となり、最小値は0である。
(行の制限と列の制限をそれぞれ設定するという考え方をみやすくするため、さらに整理、一般化するのは省略)
4. 距離の制約
3.巡回制約に加えて、最小距離を求めるための制約をつける。(基本的な巡回セールスマン問題)

例えばA→B→C→D の順番で回った時には距離が 8 + 6 + 7 = 21 となるが、これを制約とする。
A→B の順番で進んだときに、距離8の重さがかかるようなコスト関数H_abを考えると、
「A ( q[0][i] ) が1~3番目にあって、次にBが来る ( q[1][i+1] ) 」パターンを全て足し上げればよいので
H_ab = (q[0][0]*q[1][1] + q[0][1]*q[1][2] + q[0][2]*q[1][3]) * 8
これを全てのパターン足し上げればよいが、同じくループ処理を使いたいので距離の行列を
dist = [
[0, 8, 2, 9],
[8, 0, 6, 3],
[2, 6, 0, 7],
[9, 3, 7, 0],
]
と設定しておけば、距離の制約によるコスト関数 H_dist は
H_dist = 0
for i in range(4):
for j in range(4):
H_dist += (q[i][0]*q[j][1] + q[i][1]*q[j][2] + q[i][2]*q[j][3]) * dist[i][j]
となる。
また、巡回することに対しては 3. 巡回制約と同様に考えて、目的関数 H_travel は、
H_travel = 0
for i in range(3):
H_travel += (q[i][0] + q[i][1] + q[i][2] + q[i][3] - 1) ** 2
for j in range(3):
H_travel += (q[0][j] + q[1][j] + q[2][j] + q[3][j] - 1) ** 2
となる。
ここで、最終的な目的関数 H を H = H_travel + H_dist としてしまうと、最小値を取る値がおかしくなってしまう。
今回の問題設定で最短となる経路は
A → C → B → D(または全く反対方向に、D → B → C → A)であるため、
\displaylines{
H\_ \text{travel} = 0 \\
H\_\text{dist} = 2 + 6 + 3 = 11
}
の場合にHが最小となるのが正しい。
しかし「4箇所回らない」経路、例えば、A → A → C → D という経路を考えると、
\displaylines{
H\_ \text{travel} = 1 \\
H\_\text{dist} = 0 + 2 + 7 = 9
}
となる。そのため、目的関数を H_travel + H_dist としてしまうと、A → A → C → D の方が目的関数は小さくなってしまう。
これは最短距離を通ることによるエネルギー利得より、「4箇所回る」ことによるエネルギー利得が小さくなってしまっているからである。
(本当は「4箇所回る」方が優先 = エネルギーが低くなるべき)
そこで目的関数を設定する際に、巡回の制約(H_travel)を、距離の制約(H_dist)より「強い」ルールとするために、任意の重みをつける。
この重みの設定方法はある程度辻褄が合えば(※)問題ないので、目的関数は例えば
H = H_travel + 0.001 * H_dist
とすればよい。
※ H_travelの取りうる値は、小さい方から 0, 1, ...なので、0 と 1 の差「1」を区別できるような重みと距離になればよい。今回の距離は最大でも 9$\times$3 = 27 なので、重み0.001を設定しておけば、(重み)$\times$(距離) < 1 となる。
今回の経路は3本だけだが、組み合わせが増えると経路が増え、距離が指数関数的に増大する。
桁落ち等の問題から重みは無制限に設定できないので、必要に応じて正規化などを導入する。
5. 距離の制約(等号)
次は合計距離がちょうど「13」になる経路を求めるとする。
わざわざ章分けしたが、やることは1. 数量制約と同じように
(距離 - 13)** 2
の形を作ればよい。
距離について、4.距離制約で最小化しようとしており、H_dist がそのまま距離を表す。
そのまま利用すれば、目的関数は以下となる。
H_travel = 0
for i in range(3):
H_travel += (q[i][0] + q[i][1] + q[i][2] + q[i][3] - 1) ** 2
for j in range(3):
H_travel += (q[0][j] + q[1][j] + q[2][j] + q[3][j] - 1) ** 2
total = 0
for i in range(4):
for j in range(4):
total += (q[i][0]*q[j][1] + q[i][1]*q[j][2] + q[i][2]*q[j][3]) * dist[i][j]
H_dist = (total - 13) ** 2
H = H_travel + H_dist
6. 距離の制約(不等号)
最後に、合計距離が 12 以上 15 以下となる経路を求めるとする。
数式で書くと $12 \leqq$距離$\leqq 15$だが、今回距離は整数値しかとらないので、12, 13, 14, 15 のいずれかであると考える。
さらにここで、補助(量子)ビットを導入する。
今回距離の取りうる値は、12, 13, 14, 15 の4パターンあるので、s[0], s[1], s[2], s[3] の4つの補助ビット(s[i] = 0 or 1)を用意する。
距離が12, 13, 14, 15のどれかになるとき、補助ビットを使って
\displaylines{
1. ( \text{距離} - 12 * s[0] - 13 * s[1] - 14 * s[2] - 15 * s[3] ) ^ 2= 0 \\
2. ( s[0] + s[1] + s[2] + s[3] - 1 ) ^ 2 = 0
}
の2つの式が同時に成り立つと考えることができる。
これは s[0] ~ s[4] のいずれか1つが「1」であり(One-hot エンコーディング)、他のビットが全て「0」の時に、成り立つ。
以上を踏まえ、補助ビット s[i] を利用した目的関数は以下となる。
H_travel = 0
for i in range(3):
H_travel += (q[i][0] + q[i][1] + q[i][2] + q[i][3] - 1) ** 2
for j in range(3):
H_travel += (q[0][j] + q[1][j] + q[2][j] + q[3][j] - 1) ** 2
total = 0
for i in range(4):
for j in range(4):
total += (q[i][0]*q[j][1] + q[i][1]*q[j][2] + q[i][2]*q[j][3]) * dist[i][j]
H_dist = \
(total - 12 * s[0] - 13 * s[1] - 14 * s[2] - 15 * s[3]) ** 2 + \
(s[0] + s[1] + s[2] + s[3] - 1) ** 2
H = H_travel + H_dist
まとめ
- 量子アニーリング方式は、量子ゆらぎを利用して最適解を探索する手法
- QUBO形式は、量子アニーリング方式で問題を解くための基本的な表現方法
- 問題の解を 0 と 1 で表現するように、現実の問題を変換する
- 制約を考慮し、目的関数を立式する
- One-hotエンコーディングや行列、補助ビットをうまく使って制約を表現
- 必要に応じて重み付けをする
- 作成した目的関数を量子アニーリング等の実機に渡して、最小となる解を求める
QUBO式について、主に以下のサイトを参考にさせていただきました。
[1] https://qiita.com/nukipei/items/66ec2119bc0f80e9f117
[2] https://vigne-cla.com/21-12/