ゆるふわ自然言語処理（その３）Shallow Learningで文書分類

夏休みの自由研究を応援しようかと思っていたのだが、北海道は既に夏休みが終わってしまった！（北海道はお盆明け１週間で夏休み終了）

先に言っておくと、すご〜く長い記事になっております。私の夏休み自由研究発表ということで。

シリーズ目次

• MeCab で形態素解析
• fastText で単語分散表現
• Shallow Learning で文書分類　←　イマココ

今回言いたいこと

• Deep Learning じゃなくても、Shallow Learning でもそこそこ出来るよ！
• 学習自体は超便利な機械学習パッケージを使えば数行で書けちゃうよ！
• でも、前処理とか学習の方針の策定とか、考えるべきこと・やるべきことは腐る程あり、いくらでも改善できるよ！

Shallow Learning とは

まぁ造語なんですけどね。

Neural Network を使うのが Deep Learning ならば、使わないのが Shallow（浅い） Learning だろうと。でもググるとそれなりのサイトがヒットするので、私だけの造語ではないだろう（希望）。

Deep Learning がもてはやされている昨今だけれども、何でもかんでも Deep 使ってやろうとする風潮は嫌いです。Shallow だって良い所があるし、Shallow にしか出来ないこともある。

• Shallow Learning
  • Neural Network を使わない
  • 数学的・統計学的に問題を解く
  • （Deep と比べれば）実装が簡単
  • （データ量にもよるけど、Deep と比べれば）学習に要する時間が短い
  • （一般的には）CPU だけで学習・予測が可能
  • （一般的には）特徴量エンジニアリングが必要
  • Hyper Parameter の探索が必要
  • Cross Validation 等の過学習を防ぐ手法が必要
  • Hyper Parameter を使って、わざと過学習気味にするなどの微調整が可能
• Deep Learning
  • Neural Network を使う
  • Neural Network を使い、ネットワークで脳の仕組みを模して解く
  • （Shallow と比べれば）実装が難しい
  • （一般的には）学習に要する時間が長い
  • （一般的には）学習には GPU が必要
  • （一般的には）特徴量エンジニアリングは不要
  • Hyper Parameter に代わる、アーキテクチャの最適化が必要
  • Gradient Discent, Dropout など、過学習を防ぐ機構がモデル内に含まれるため、（一般的には）過学習を防ぐ手法は不要
  • （一般的には）微調整は難しい

機械学習には大きく分けて以下の種類がある（強化学習とか例外もあるけど）。基本的に下に挙げたものほど難しい。

• Classification（分類）
  • 教師あり学習（Supervised Learning）
  • データのラベル（カテゴリ）を予測するもの。教師データはそのラベル
• Regression（回帰）
  • 教師あり学習
  • データの値を予測するもの。教師データはその値
• Clustering
  • 教師なし学習（Unsupervised Learning）
  • データをいくつかのクラスタに分けるもの
• Generation（生成）
  • 半教師あり学習（Semi-Supervised Learning）
  • 実在しない人の顔画像を作ったり、写真をモネ風に変換したり

ということで、今回は Shallow Learning を使って NLP、その中で最も簡単な問題である文書分類を行う。最も簡単な、と言っても馬鹿にしたものではなく、すぐに実務に使える可能性があるものだ。

やってみた

ということで、今回も既にやっております。

データとして livedoor news corpus を使っている。日本語の文章で何かしたいという時には毎度お世話になっている。

livedoor news corpus は 2012 年あたりに収集された、その当時の livedoor news で掲載していた各雑誌の記事をまとめたもの。記事の文書から雑誌に分類することを目的とする。

上記のリンクは Gist なんで、クリックすれば何やってるのかは全部見れます。ここを読む必要は特に無い。なので、この Qiita 記事は具体的な動作ではなく、概念的なものの解説をしようかと。

ちなみに上記 Gist をダウンロードして、自分で Jupyter の環境を作れば、みなさんの手元でも勿論動きます。（Python の仮想環境は好きなように設定した上で）以下のコマンドを叩けば良いんじゃないかな。

> pip install jupyterlab numpy scipy scikit-learn matplotlib seaborn pandas simplejson mecab-python3 gensim neologdn 

ということで解説していきますが、話の流れの都合上、実際の処理の順番とは異なる順番で書いていくので、そこは注意されたし。

泥臭い前処理

機械学習をやる前には泥臭い前処理がいつも付き纏う。特に NLP の場合はテキストファイル、すなわち構造化されていない（内容の形式が決まっていない）データなので苦労することが多いし、そもそも好き勝手書かれている文章（喋り言葉、ネットスラング、絵文字・記号、箇条書き、括弧の違い等々）を解析するのはとても大変。

今回やっている前処理は以下。

• テキストが格納されているディレクトリ名からカテゴリ（掲載されている雑誌）を取得
• ファイル名からIDを取得
• どこにも説明は無いけど、ファイルの中身を読んで、以下のフォーマット（らしきもの）があることを発見したので、その通りに読み込む
  • １行目：記事のURL
  • ２行目：記事が投稿された時刻
  • ３行目：記事のタイトル
  • ４行目以降：記事本文
• 記事本文から、記事に直接関係ない部分をなるべく自動的に削除する
• 文章の正規化
  • 形態素解析辞書として IPA-NEologd ベースのものを用いているので、neologdn を用いて正規化する
  • 形態素解析辞書として用いているのは私が作成したもの
    • https://github.com/tetutaro/mecab_dictionary
    • （2023/02/03 追記）上記辞書はかなり古くなったので削除したので、その代わり下記の辞書を使ってください
    • https://github.com/tetutaro/mecab_dictionaries
    • 上記の repository についての記事はコチラ
  • Wikipdiaを学習した単語分散表現（FastText）でも同じ形態素解析辞書、neologdnを使っている
    • https://github.com/tetutaro/fasttext_binary_jawiki
  • neologdnでも「“」（全角左ダブルクオーテーション）は「"」（全角ダブルクオーテーション）に変換されないので、これを明示的に（neologn.normalize()する前に）変換する
• 特徴量エンジニアリング

特徴量エンジニアリングについては後述するので、それを除いた中で一番苦労したのは４つめの項目。記事に直接関係ない部分の削除。

こんなことをやっている。

• 「Amazon.co.jp で詳細を見る」という文は、記事で紹介した商品へのリンクであり、共通しているので、削除する
• httpから始まる文はリンクURLなので、削除する
• 関連記事もしくは関連リンク・関連情報の行以降は、その記事の関連記事へのリンクなので、削除する
  • 関連記事などの前後の記号には様々なパターンが有り、記号を特定して削除することは出来ない
  • 本当に文章中に関連記事などの単語がある場合があるため、ある文字数(20)未満という判定条件を付ける

削除のルールをひとつ付け足すたびに、全部のデータの処理結果を見て「必要なものまで削除してないか」「もっと削除すべき箇所はないか」というのを確認しながらやっている。なので地味だけど、とても時間がかかるし、大変。

でもこれで最終形かというと、そうではないと思う。もっと削らなければならないこともあると思うし、もっとスマートなやり方もあるかもしれない。やればやるだけ予測の精度が（ほんの少しだろうけど）上がるだろう。みなさんがやる時には、是非もっと良い方法を探してほしい。

もちろんこのデータで通用したやり方は、違うデータでは通用しないだろう。データが来るたびに毎回こんなことやっている。これが「デェタサイエンティスト」だ。

特徴量エンジニアリング

前処理の一部だけど、これだけで内容がかなり多いので、別の章立てにする。

今回は Shallow Learning を使うので、文書を数字の列（ベクトル）に変換しなければならない。文書をテキストに変換する方法は、主に以下の２種類。

• 文書に出てくる単語の出現回数でベクトル化する
  • Count Vector
  • TF-IDF Vector
• 単語分散表現を使う
  • SENTENCE2VEC, DOC2VEC
  • WORD2VEC

Count Vector は、その名の通り、文書中で単語が出現した数をベクトルとする。

• 吾輩は猫である
• フランダースの犬と名犬ラッシー
• 犬と猫が仲良く寝ている

これらの文書から「犬」と「猫」だけをカウントした場合にはそれぞれ以下になる。

• {"犬": 0, "猫": 1}
• {"犬": 2, "猫": 0}
• {"犬": 1, "猫": 1}

もちろん上記は説明のため「犬」と「猫」しか取り出さなかったけど、本当はもっと沢山の単語でやるべき。

TF-IDF はこれをもっと賢くしたもの。Wikipedia とか scikit-learn の説明（英語）等を見てくれ。

単語分散表現はゆるふわ自然言語処理（その２）で説明した。その２では単語をベクトル化する WORD2VEC しか扱わなかったけど、実は文章をベクトル化する SENTENCE2VEC、文書をベクトル化する DOC2VEC もある。

全部やってみて一番良い方法を選ぶことが一番良い。みなさんがやる時には是非色々試して欲しい。

ベクトル化の方針

TF-IDF Vector と WORD2VEC の２種類をやろうと思っていたのだが、面倒くさいからひとつに絞ることにする。それぞれの特徴は以下。

• Count Vector, TF-IDF Vector
  • 単語をモロに使うので（そのまま圧縮しないで使うならば）どの単語が影響したのか分かる
  • でもベクトルの長さ（次元数）が使用する単語数（一般的には数万個）にもなってしまい、次元の呪いの影響をモロに受ける
  • 新しい文書に新しい単語が出てきた場合、その単語を使えない
• SENTENCE2VEC, DOC2VEC
  • 単語を低次元ベクトルに埋め込むので、どの単語が影響したのかは分かりにくい
  • ベクトルの長さは適度（300次元程度）に抑えられる
  • 新しい文章・新しい文書を予測したい場合には、一般的に再学習が必要
• WORD2VEC
  • 単語を低次元ベクトルに埋め込むので、どの単語が影響したのかは分かりにくい
  • ベクトルの長さは適度（300次元程度）に抑えられる
  • Wikipedia 等を学習することにより、出現しそうな単語を予め学習しておくことで、学習した文書に無い単語にも対応できる
    • もちろん WORD2VEC の学習から漏れた、そもそも Wikipedia にも載ってない等の理由で、対応出来ないものもある

ということで、WORD2VEC を使うことにする。

単語の削除

TF-IDF を使うにせよ WORD2VEC を使うにせよ、文書分類は「単語の共起」（違う文書に同じ単語が出現すること）を学習するものだ。（WORD2VEC の場合は単語ではなく単語が埋め込まれたベクトルの各次元の共起になるが）

分かりやすい例で言うと、「野球」という単語がある文書は「スポーツ」に関するものだ、というような。

共起を学習する場合、必要無い単語を削って、分析結果を明確にする、予測の精度を上げることが一般的に必要だ。

単語の削り方には以下がある。

• 文書の意味に影響を与えない品詞である単語を削除する
  • 接続詞・助詞等は明らかに文書の意味に関与しない
  • 未知語（形態素解析で辞書に存在しないとされた単語）は大抵の場合は名詞扱いだが、これを削除するかしないかも判断が必要
• 公開されている "stop words" を削除する
  • stop words: 非常に頻繁に使われるため、削除したほうが良いと一般的に考えられているもの
  • 各言語（日本語、英語、etc...）毎に、色んなものが公開されている
• 文書頻度（DF: Document Frequency）が高いものを削除する
  • その単語が文書全体の何割に出現するか
  • 多くの文書に出てくる単語を使っても、その文書の特徴を表さないため、邪魔
• 文書頻度が低すぎるものを削除する
  • ほんの少し（数個）の文書にしか出てこない単語は、形態素解析の誤分類の可能性があるし、その文書に特有すぎて解析が難しい
    • そもそもそういう単語こそが大半なので、全部扱うのはやってられない
• ひらがな一文字・カタカナ一文字を削除する
  • もちろん日本語の場合
  • 箇条書きの記号とかである可能性もあるし、形態素解析の誤分類の可能性もある
  • アルファベット一文字も削除した方が良いかも
• 数字・漢数字を削除する
  • 数字は基本的には「文書の意味」には関与しない
    • 数字の値が何らかの意味を保つ場合には、削除してはいけない
  • 数字・漢数字一文字の場合の方が良いかも
• 形態素解析辞書の癖で、明らかに誤分類であると思われるものを削除する
  • 特に形態素解析で変化形を原形に戻した場合

改めて書き出すと、いっぱいあるなぁと実感する（小並感）。

これも、削ってみては「大切な言葉を削ってないか」「もっと削るべきではないか」と確認するし、実際に学習してみて精度が悪い場合・もっと精度を上げたい場合に結果を解析して繰り返し試行錯誤するので、何をやるかどうやるかを決めるのに非常に時間がかかる。

今回は、まず品詞による削除を行う。具体的には、名詞・動詞・形容詞以外は全部削除（IPA辞書を使うので、形容動詞は名詞に含まれる（名詞 > 形容動詞語幹））。名詞にも色々あるので、Type 2 を使ってもっと狭く絞り込むべきかもしれないが、今回はやらなかった。
また、未知語は削除した。

そして Wikipedia を学習した WORD2VEC を使うので、そもそも学習できなかった（意味が分からない）単語は除外する。

次は stop words。
一般的によく参照されている stop words は SlothLib だろう。Kaggle に投稿されている Japanese stop words なんてものもある。だけどまぁこういうものは次の文書頻度でたいていは落とせるので今回は省略した。もちろん何らかを使った方が良いだろう。

次に DF が高いものを削るやつ。
Wikipedia には TF（Term Frequency：単語頻度）, IDF（Inverse Document Frequency：逆文書頻度）, TF-IDF の計算式は載っている。DF はどうかというと、もっと簡単。

\mathrm{df}_{i} = \frac{|\left\{d:d\ni t_i\right\}|}{|D|}

分子の $|D|$ は総文書数、分子のなんやかんやは単語 $t_i$ を含む文書数。これは「その単語が文書全体の何割に出現するか」以外の何者でもない。
そして、どのくらいの DF なら消すかという閾値調整は毎回難しい。
今回は雑誌の種類が９種類ということで、1/9 ≒ 0.11 を閾値とした。
「ある単語は、その雑誌の記事には毎回登場するが、他の雑誌の記事には全く出ない」という理想的な状態を考えると、その DF は 0.11 だからである。
実際にこの操作で削除された単語を見ると、なかなか良い感じに消せていると思う。
今回は sklearn.feature_extraction.text.TfidfVectorizer() の max_df オプションを使って、DF が高いものを TfidfVectorizer.stop_words_ に列挙した。実は後 TdidfVectorizer.transform() をするだけで TF-IDF Vector は作れる状態だった（でも使っていない）。

次に DF が極端に低いものを削るやつ。
今回は WORD2VEC で学習出来なかった単語は削ってあり、学習できた単語はベクトルに変換できるので、特に削除しなかった。
DF が低い単語を見ると、まぁ酷い単語が並んでいるので、削った方が良かったかもしれない。
削るとしたら文書10個分に相当するぐらいの値を閾値として設定すれば良いのかと考える。
実際にやる分には sklearn.feature_extraction.text.TfidfVectorizer() の min_df オプションで実装すれば良い。

ひらがな一文字・カタカナ一文字は削った。
数字・漢数字は削らなかった。
Wikipedia を学習しているので、学習した単語として例えば「1g」なんて単語も含まれてしまうので、一概に削除するのもどうかと。
これら「先頭が数字となっている単語」を一括して削ってしまっても良かったかもしれない。また「先頭がマイナス付きの数字となっている単語」も同様に削ってしまっても良かったかもしれない。

最後に、形態素解析の癖で誤変換される単語。
これはもう辞書の癖で、何回も繰り返し使っていって把握するしか無い。
今回の形態素解析の辞書では、「ないしは」という接続詞があった場合、これを「内侍」という名詞と「は」という接続詞のペアと見なしてしまう。だから単語を原形に直したものを見ると、聞き覚えのない「内侍」という単語がそこかしこに現れてしまう。よって、この単語を削除する。

ということで、考えるべき事もやるべき事も非常に多いので、みなさんがやる時には是非色々試して欲しい。

変化形のまま？原形にする？

さらっと上で「原形に直す」と書いたが、実は大きな問題。

ご存知の通り、動詞など変化形がある品詞は文章中では未然形・連体形など変化形で現れることがある。これを原形に直して学習すべきか、それとも変化形のまま学習すべきか。

探す限り、どうすれば良いかという王道は存在しない。

単語分散表現において、変化形の意味も含めた学習をしたい場合は、変化形のまま学習すべきだろう。例えば「走った」という単語は「走る」＋過去形の意味を持つという解析を行いたい場合。

しかし、原形を使うと、より多くの単語が「同じ意味である」と認識されるので、文書分類のような共起を学習する場合には有利になると考える。

使う辞書にも依存すると考える。
Juman 辞書は「走った」のような変化形の語尾まで単語として認識するのに対し、IPA 辞書は変化形の語尾を別形態素として分割するという特徴がある。

> echo "私は走った" | mecab -d /usr/local/lib/mecab/dic/jumandic
私    名詞,普通名詞,*,*,私,わたし,代表表記:私/わたし 漢字読み:訓 カテゴリ:人
は    助詞,副助詞,*,*,は,は,*
走った 動詞,*,子音動詞ラ行,タ形,走る,はしった,代表表記:走る/はしる
EOS

> echo "私は走った" | mecab -d /usr/local/lib/mecab/dic/ipadic
私    名詞,代名詞,一般,*,*,*,私,ワタシ,ワタシ
は	    助詞,係助詞,*,*,*,*,は,ハ,ワ
走っ   動詞,自立,*,*,五段・ラ行,連用タ接続,走る,ハシッ,ハシッ
た    助動詞,*,*,*,特殊・タ,基本形,た,タ,タ
EOS

ということは、IPA 辞書の場合は「過去」という意味が「た」という助動詞に与えられてしまっていると考えることも出来るだろう。

今回は、WORD2VEC で Wikipedia を学習する時も、livedoor news corpus を分析するときも、すべて変化形がある品詞は原形に直して学習した。

今回の為に、fasttext_binary_jawikiに原形に直して学習するオプションを追加し、学習し直した。

これも、みなさんがやる時には是非色々試して欲しい。

文書を表すベクトルの算出

まだ終わりではない。

文書を形態素解析で単語に分解し、不要な単語を十分に削除して、WORD2VEC を使って単語をベクトルにした。
するとある文書（記事）に対して、いくつものベクトルが出来る。
欲しいものは、ある文書に対してひとつのベクトル。
これら沢山の単語ベクトルをどうすれば「文書の意味を示すひとつのベクトル」に出来るのか。

平均とれば良いんじゃね？って思うでしょ。正解なんだけど。

何がしたいかというと、文書中に現れたいくつもの単語ベクトルの「真ん中」を取れば、それがその文書の意味を表すベクトルになるんじゃね？っていう直感的な方法。分かりやすいし、それ以外に特に思いつかない。文書から余計な意味を削ろうと、単語を削るのに大変な思いをしたんだし。

単語分散表現（WORD2VEC）で、単語間の意味の近さはコサイン距離で表されると言われている。意味的な「真ん中」を取りたいのなら、コサイン距離の「真ん中」を取ればいいんじゃないか。

真ん中って何だ。平均だ。中心だ。中心って何だ。重心だ。

重心って、正確に言うと、フレシェ平均のこと。
これは何かって言うと「分散が最小になる点」。
平面上にバラバラに散らばっている点を考えると、その平面のどこかに点の分散がピタリと０（最小）になる点がある。だから釣り合う。それが重心。意外と簡単に納得できる話ではある。

で、このフレシェ平均は、普通のユークリッド距離を使う分には単純に平均。何も難しいことはない。
しかし、違う距離を使う時には異なる値になる。
じゃあコサイン距離のフレシェ平均って何だ、ってことになるのだが、「よく分からない」が答え。

そもそもコサイン距離ってコサイン類似度の逆（1 - コサイン類似度）を便宜的に名付けているだけで、正確に言うと距離ではない。距離の定義の三角不等式を満たさない。だからコサイン距離のフレシェ平均は、どこかに存在するだろうけど、それをビシッと表す式は無い。

ちなみに、これを効率的に計算するアルゴリズムの論文はある。こういう頭の良い人に私はなりたい。

閑話休題。じゃあどうするのか。

• 各単語のベクトルを正規化（長さを１に）する
  • ベクトルの各要素をベクトルの長さ（２次元のユークリッドノルム）で割る
• それらを足し合わせて普通に平均を計算する

これだけ。何でこれでいいの？これで大丈夫だってみんな言ってるから。

単語分散表現って、そこそこ上手くいくし面白いけど、何でそれでいいの？ってなると「出来てるからい〜じゃん」ってのが結構多い。そこがまた良いんだけどね。まぁ、それで言ったら Deep Learning だって（あれ？誰か来

機械学習の前のデータ整形

まだ終わんないんだよ。まだ学習出来ないんだよ。

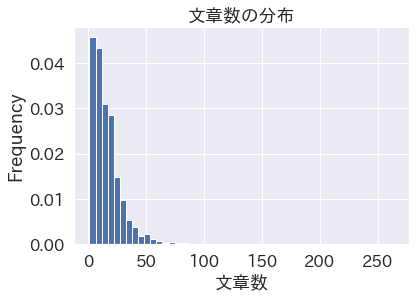
分布の確認

データを作ったら、なにはともあれ分布を確認する。これはデェタサイエンティストの義務。

この時点で考えられる分布としては、以下がある。

• 各単語の出現回数の分布
• 各文書の文章数の分布
• 各文書の単語数の分布

単語の出現回数（要するにDocument Frequency）は、単語を削除する所でいっぱい考えたので、もう良いとする。
後は文章数の分布と単語数の分布。

これらを見ると、「両方とも、べき分布っぽいなぁ」と思う。

分布は、だいたい以下の３種類に分かれる。

• 正規分布（ガウス分布）
  • いわゆる、山の形。平均の値がそこそこ大きい
  • 扱いやすい。意味を取りやすい
• ポアソン分布
  • ０に偏った山。平均の値が小さい
  • あまり起こらない事象が従う分布。扱いは少し難しい
• べき分布（Zipf分布）
  • ｘ軸とｙ軸にひっつく感じ。両対数を取ると直線っぽくなる
  • 自然界に存在するものが従う分布。扱いは非常に難しい

上記のように、分布を見るだけで問題の難しさがある程度分かる。（統計学には、その分布に本当に従うのかを判断する各種検定があるが、大体の形や特徴が分かれば良いので、そこまでする必要は無い）

でまぁ今回は、文章数や単語数の分布なんで、やっぱりべき分布っぽくなっている。これらの値を直接使う訳ではないので、まぁ良いとしよう。

異常値の判断と削除

分布を見て分かることは、その性質だけではなく、例えば異常値も分かる。

今回で言えば、記事が０行のもの、０単語のもの。これは前処理の中で弾いちゃってるけど、非常に少ないものは異常な記事として良いだろう。

こういうのを見つけるためには、分布を描くだけじゃなくて、各種統計値を見ることも大事。pandas.DataFrame を使っているのであれば、pandas.DataFrame.describe() と１行書くだけで計算してくれる。

これを見ると、記事の文章数が１行のものもあるみたいだけど、長い１行ならば記事としてアリなので、これは良いとしよう。

しかし、記事の単語数が１個のものもある。これは流石にマズい。単語を削りすぎたせいなのかなと思ったけど、実際の記事を見ても本当に１単語しかなかった。

こういうものをそもそもデータから除外しよう。異常値データの削除だ。
この時に問題となるのは、果たしてどの値を閾値にして異常値と判断し、そして削除するのか。

最も簡単で基本的な異常値の判断は、箱ひげ図の書き方に従うこと。
ということで、本当は箱ひげ図を描くべきなんだけど、べき分布的な分布をするので、単語数が多い記事があって箱が潰れて、まともな図にならないので省略した。なので一般的な箱ひげ図で説明する。

箱ひげ図の箱は、上四分位点と下四分位点の範囲を表す。箱の中の線は中央値（mean（平均） ではなく median）。pandas.DataFrame.describe() で言う所の 25%, 50%, 75%。箱ひげ図の髭は、上四分位点・下四分位点からさらに 1.5 * IRQ（四分位範囲）だけ伸ばしたもの。下の髭なら1.5 * (50% - 25%）、上の髭なら 1.5 * (75% - 50%)。この髭にも収まらない点が異常値。

この場合で計算すると、下の髭の先がちょうど 35 だったので、単語数が 35 未満の記事を削除した。

じゃあいつも箱ひげ図を書いて、髭に収まらないデータを削除すれば良いかというと、そうではない。

今回のデータでも、単語数の多い方の記事は削除してない。長い文章の記事は別に異常というわけではないから。それにそもそもべき分布なので、単語数が多い記事があるのは当然とも言える。

このように、何が異常なのかを判断するためには、そのデータの意味や分布を理解しなければならない。

学習用データと検証用データの分離

Machine Learning で一番怖いのは、過学習。

あるデータを学習して良い精度が出た。だけど実際に動かして、日々新しく生成されるデータでやってみたら、結果はメタメタだった。こんなケースがある。
学習に使った（過去の）データで学習するときに、たまたまその学習データに現れた特徴を追いすぎてしまい、違うデータ（新しいデータ）ではそんな特徴は無いので全然正解しない、という状態。
これを過学習と言う。

要するに、マンモスは牙が長いほうがモテモテなんで、どんどん牙を長くしてったら、逆に長過ぎて滅亡しちゃったね、って感じ。（マンモスの牙は俗説です）

過学習が起きていないかチェックするために、データを学習用データ（TRAIN）と検証用データ（TEST）に分離して、TRAIN だけを使って学習し、TEST で予測する。そしてその TRAIN と TEST の精度を比較する。TRAIN の方が明らかに高かったら、過学習。同じぐらいだったら、良い感じ。

これは必ずやらなければならない。データを分離するのは面倒くさそう。でも sklearn.model_selection.train_test_split() という便利関数があるので簡単に出来る。

ここで本来ならば、TRAIN と TEST は全く同じ分布にしたい。
全ての特徴、全ての結果が TRAIN と TEST で全く同じ分布、強いて言えば、これから生成される未来のデータもこれらと全く同じ分布である方が良い。なぜなら分布が違うと予測結果も違うはずだからだ。

極端な例を挙げると、TRAIN にスポーツの記事がひとつも入っていないように分離してしまったとする。
TRAIN にスポーツの記事がひとつも入っていないので、当然スポーツの記事であると学習し予測することは出来ない。だから TEST に入っているスポーツの記事は全て間違えてしまうことになる。

しかし、TRAIN, TEST と分けたすべてのデータを両者で同じ分布にすることは、ほぼ不可能。そんなに上手い分け方を見つけるのは学習するより何倍も大変だろう。ましてや将来のデータの分布なんて分かりようが無い。なぜなら母集団というのは世の中に存在する全てのデータを取ってこなければ厳密には分かりようがなく、そんなことは一般的には不可能だからだ。（そこを何とかするのが統計学なんだけど）

だからこそ、せめて Classification、特に教師データであるカテゴリの分布ぐらいは TRAIN, TEST で同じような分布にしたい。これが sklearn.model_selection.train_test_split() における stratify だ。これに教師データ（カテゴリ）を与えることで、なるべく TRAIN, TEST でカテゴリが同じような分布になるよう分けてくれる。

以下に述べる Cross Validation でも、sklearn.model_selection.KFold の代わりに sklearn.model_selection.StratifiedKFold を使っていることで同じことを実現している。

再現性の確保

sklearn.model_selection.train_test_split() には random_state というパラメータがあり、Gist ではここに適当な数字を与えている。

これ、実はすごく重要。

Data Scienceも Science の一種なので、再現性がなければならない。再現性が無いものは科学ではない。
例えば、ある予測モデルを作った。とても精度が良かった。いざこれを本番で使おうって時に、うっかり間違えて学習したモデルを消してしまった。じゃあ作り直そうとやってみても、同じものが一向に出来ない。ってなったら困るのは明らかな訳で。

再現性が無くなってしまう原因は、手法やモデルに乱数を使うものがあるから。これが本当にランダムだったら、いくらやっても再現はしない。
乱数に必要なことは、例えば 0 以上 1 以下の乱数を 100 個作るとすると、作った100 個の乱数が 0 から 1 までの間の値を満遍なく取ること（一様分布に従う乱数）。100 個の乱数のうち 90 個が 0.9 以上の値だった、なんてのは乱数じゃない。逆に言えば、そういう性質を持つ値だったら、決まった値のものを使っても良い。

scikit-learn(sklearn) における random_state は、この乱数の種（seed）を与えるもの。

>>> import numpy as np
>>> np.random.rand(3)
array([0.23593267, 0.48725524, 0.9374448 ])
>>> np.random.rand(3)
array([0.63444953, 0.02204021, 0.56938029])
>>> np.random.seed(12)
>>> np.random.rand(3)
array([0.15416284, 0.7400497 , 0.26331502])
>>> np.random.seed(12)
>>> np.random.rand(3)
array([0.15416284, 0.7400497 , 0.26331502])
>>> np.random.rand(3)
array([0.53373939, 0.01457496, 0.91874701])

numpy での例だけど、乱数を生成する関数（numpy.random.rand()）を普通に叩くと、毎回違う値が生成される。
ところが種を設定してあげる（numpy.random.seed()）と、何回叩いても同じ値が返ってくる。（seed を設定しないと「その次の乱数」が生成されるので、違う値になる）

このように種を設定すれば、乱数を使う手法・モデルでも再現性が確保できる。
なので、種を設定しない人はデェタサイエンティスト失格なのであります。

• どこで使うか分からないので、random.seed() と numpy.random.seed() は最初に必ず設定しておく
• scikit-learn(sklearn) の関数・モデルの中で　random_state がオプションにあるものは、すべて何らかの値を設定する

ところで私は Gist の中で random.seed() と numpy.random.seed() を設定し忘れているので、私はデェタサイエンティスト失格なのであります。

学習

やっと学習に入るよ・・・

モデル

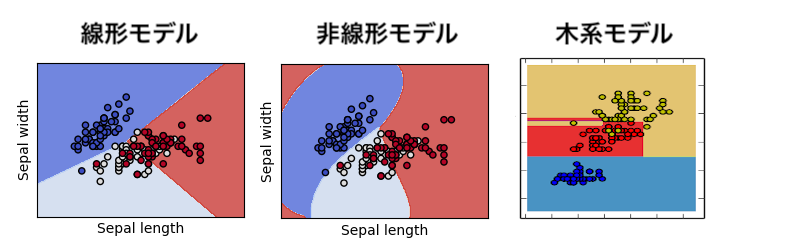
Shallow Learning は線形モデルと非線形モデルに大別できる。

• 線形モデル
  • データをスパッと直線で切る
  • 代表：Support Vector Machine (SVM)
• 非線形モデル
  • データをグネグネと曲線で切る
    • 面をゴムのようにビョ〜ンと引っ張った上でスパッと切る
  • カーネルを用いた Support Vector Machine
• 木系モデル（非線形モデル）
  • ２分木で、データを２つ、更に２つ、更に２つ、と切っていく
    • 結果的に、凸凹しているが、これも曲線と見做すことが出来る
  • 代表：Random Forest (RF)

線形モデルと非線形モデル、両方やってみることが大切。

で、今回は線形の SVM と RF を使っているんだけど、流石にこれらのモデルを解説すると、ただでさえ長いこの記事が無限の長さになってしまう。とりあえず Wikipedia (SVM, RF) や scikit-learn (SVM, RF)、後は巷に溢れる本を読めば良いんじゃないかな。（ゆるふわ）

Hyper Parameter Search と Cross Validation

モデルにもパラメータがあり、データによってそのパラメータを調整しなくてはならない。

正確に言うと、機械学習モデルにとってパラメータと言ったらデータそのものなので、モデル自体のパラメータを Hyper Parameter と呼ぶ。（強そう（小並感
例えば Random Forest の場合、木の数・木の深さ等といったものが Hyper Parameter。

あるモデル＆データにとって最適な Hyper Parameter とは、過学習を起こさない中で最も精度が良い Hyper Parameter である。過学習を起こすか起こさないかは、Hyper Parameter で決まると言っても過言ではない。
（逆に、目的によっては、Hyper Parameter をわざと最適な状態からずらして、過学習気味にするということも出来るが、通常はあまりやらない方が良い）

ということで、Shallow Learning の場合は以下のことを何回も何回も繰り返す。

1. Hyper Parameter を何らかの値に決める
2. 学習して精度を計算する
3. 過学習をしていないかチェックする

過学習していないかのチェックとしては、学習を行う前にデータを TRAIN と TEST に分けた。これは最終確認用であって、学習の時には TRAIN を更に細かく分割して使うことになる。（だからデータはいっぱい必要！）
上記の 2 と 3 を詳しく書くと、以下のようになる。

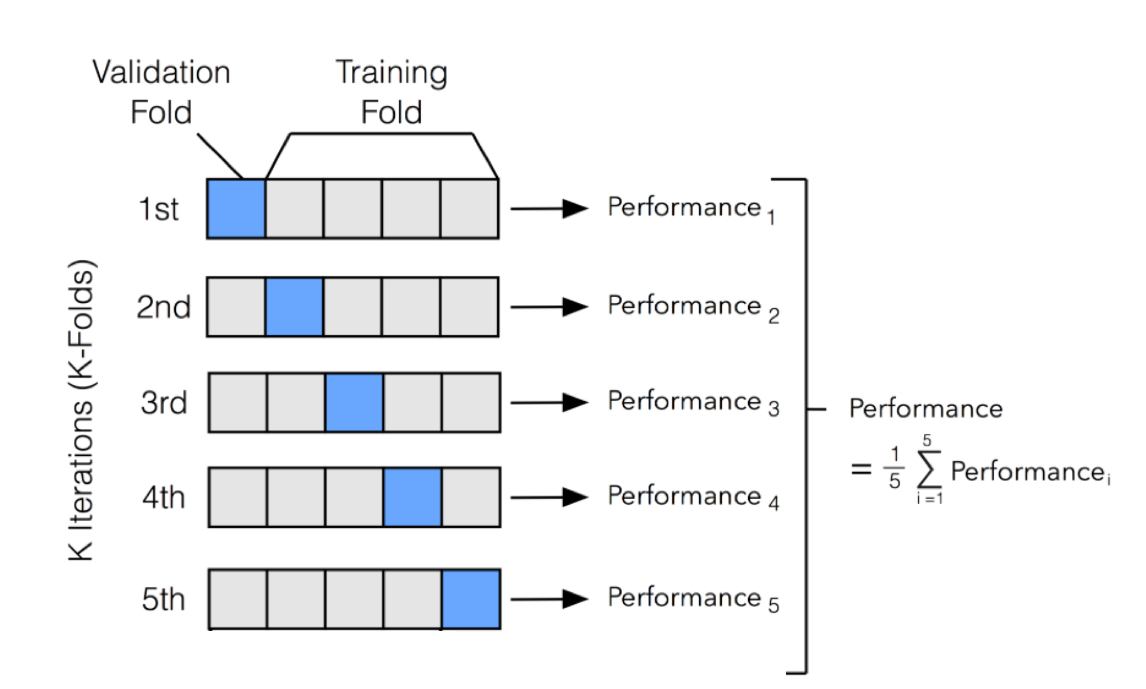
• TRAIN をさらに何個かに分ける
  • 出来れば Stratified に
  • 例えば５個に分ける
• ５個のうち４個を使って学習、１個を使って評価する
  • 評価に使うデータを「ずらす」ことによって、５通りの学習＆評価が出来る
• ５回の評価値を平均したものを、その Hyper Parameter の評価値とする

この方法を Cross Validation と呼ぶ。

Cross Validation は過学習を防ぐために必須だけれども、やっぱり学習のコストが高い（マシンパワーが必要＆時間がかかる）。だからなるべく効率よく探したい。この時に、Hyper Parameter を探す範囲をどのぐらいにして、どうやって最適な値を探すか、ということが重要になってくる。

単純な方法としては、以下の２つ。

• Hyper Parameter の範囲を等間隔に分割し（グリッド）、それらの値でやってみる
  • "Grid Search"
• Hyper Parameter の範囲からランダムに値を選択し、それらの値でやってみる
  • "Randomized Search"

ランダムで大丈夫かいな、と直感的には思っちゃうんだけど、実はランダムの方が一般的には効率が良い（より少ない回数で最適な Hyper Parameter を見つけられる）（論文）。

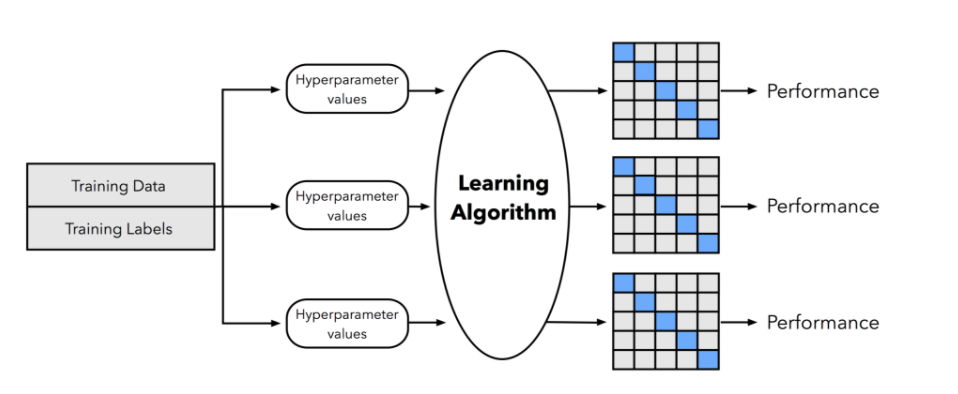
Hyper Parameter Search と Cross Validation を図でまとめると、以下のようになる。

（上記２つの図は ethen8181.github.io/machine-learning/model_selection/model_selection.html より引用）

こうやって説明すると、すごい難しそうで大変そうだけど、scikit-learn という有り難すぎるパッケージのお蔭で、なんと Python ４行で書ける。

hparams_svm = {...}
svm = LinearSVC(...)
skf_svm = StratifiedKFold(...)
hpsearch_svm = RandomizedSearchCV(...).fit(train_X, train_y)

Hyper Parameter Search は Grid と Random だけじゃなくて、近年「ガウス過程上でのベイズ最適化」とか「木構造を用いたParzen最適化」とかで、Hyper Parameter Search も学習してやろうというのが流行っている。

• 解説記事
  • Hyper-parameter optimization algorithms: a short review
• 有名なライブラリ
  • hyperopt
  • optuna
• 各ライブラリの利用方法の記事
  • Hyperopt で機械学習モデルのハイパーパラメータを選ぶ
  • Optuna で機械学習モデルのハイパーパラメータを選ぶ

何を使っても、Hyper Parameter の探索範囲は試行錯誤で決めるしかないんだけどね！
みなさんがやる時には是非色々試して欲しい。

評価

学習したら評価をしましょう。

評価指標

今まで単に「精度」と書いてきたけど、「どれだけ機械学習が良い予測をしたのか」を表す値をどのようなもの（評価指標：metric）にするのかは、とても重要な問題。

回帰（値を予測する）だったら、平均二乗誤差（MSE: Mean Squared Error）かその派生ぐらいしか選択肢は無いんだけど、分類の場合にはちゃんと意味を理解し、最適なものを選ばなくてはならない。

この指標を理解するために、まずは最も基本的な２クラス分類（Binary Classification）の場合を考える。
そして２つのカテゴリのうち、一方を目的のカテゴリとする。（例えば、病気にかかっているかいないかの分類で、病気にかかっている方を目的のカテゴリとする）

この時、実際の状態と予測結果がそれぞれ２種類、データは合計４種類に分けられる。

• 実際の状態
  • 目的のカテゴリに属している（Positive）
  • 目的のカテゴリに属していない（Negative）
• 予測結果
  • 目的のカテゴリに属していると予測した
  • 目的のカテゴリに属していないと予測した

４種類のデータは、２種類が正解、２種類が不正解（過誤）で、それぞれ名前がついている

• 正解
  • 目的のカテゴリに属していると予測して、実際に目的のカテゴリに属している
    • True Positive (TP)
      • 正しく Positive と予測した
  • 目的のカテゴリに属していないと予測して、実際に目的のカテゴリに属していない
    • True Negative (TN)
      • 正しく Negative と予測した
• 不正解
  • 目的のカテゴリに属していないと予測したが、実際には目的のカテゴリに属している
    • False Negative (FN)
      • 間違えて Negative と予測した
    • 第１種過誤（予測漏れ）
  • 目的のカテゴリに属していると予測したが、実際には目的のカテゴリに属していない
    • False Positive (FP)
      • 間違えて Positive と予測した
    • 第２種過誤（予測過多）

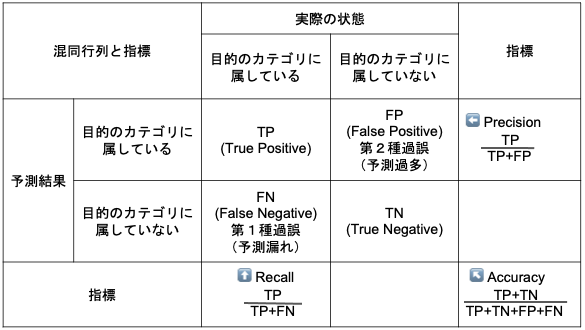
この４種類のデータを２ｘ２の表で表したものを、混同行列（Confusion Matrix）と呼ぶ。

上の表に既に書いてしまっているが、ここから３種類の指標が計算できる。式は表に書いてあるのを参照して欲しい。

• Accuracy
  • もっとも一般的な「精度」
• Recall
  • 予測過多はいくらあっても構わないが、予測漏れだけは精一杯防ぎたい場合に使う指標
  • 予測漏れのリスクが高い場合に使う
    • 例）間違って「病気だ」って言っても後で再検査すれば良いけど、病気を見逃すことだけはマジ勘弁
• Precision
  • 予測漏れはいくらあっても構わないが、予測過多だけは精一杯防ぎたい場合に使う指標
  • 予測過多のリスクが高い場合に使う
    • 例）本当は商品に興味を持っている人に宣伝メールを送らなかったというのは、ただの機会損失なので実害はないが、商品に興味を持ってない人に宣伝メールを送ってしまうと、ウザがられて逆に悪い印象を持たれちゃうので、それはマジ勘弁

ここで一番強く言いたいのは、「Accuracy は使ってはダメ」ということ。
２クラスそれぞれに属するデータの数に偏りがある（imbalance: 不均衡）場合、Accuracy は全然信用できない。

• 例えば１万個のデータのうち、10個が目的のカテゴリに属する、9990個が属さない場合
• 「何も考えずに全部目的のカテゴリに属さない」とするモデルの Accuracy
  • 9990 / 10000 = 0.999
• Accuracy は「データが偏っている」というだけで、非常に高い値を示す

一般的に、データは imbalance だ。そして大抵、データ全体の中で欲しいデータは少ない。だから Accuracy は使ってはダメ。ゼッタイ。

それに対して、Recall や Precision はそもそも TN を一切無視している（大多数である、必要無いものが当たったという無駄な正解）。だから imbalance に強い。
特にビジネスの場面では、Recall か Precision を使うべきである。なんせ簡単。そして機械学習の効果を見積もる時に、Recall と Precision はとても使いやすい。
そして Recall と Precision のどちらを使うかは、そのビジネス要件によって適切な方を採用すべきだ。（どちらのリスクがより深刻なのか）

どちらのリスクもあまり深刻ではなく、全体的に良いものを使いたいと言う時は、下に挙げた F1-score を使うべき。

表に載っていない指標で有名なのは以下。

• F1-score（F値）
  • Recall と Precision の平均（調和平均）
  • Recall と Precision がちょうど良い具合（同じぐらいの値）の時に最も高い
  • リスクをあまり気にしない場合、全体的な精度を知りたい場合に使う
• True Positive Rate と False Positive Rate
  • True Positive Rate は Recall と同じ
    • Positive の中の True Positive の割合（TP / (TP + FN)）
  • False Positive Rate は Recall の逆
    • Negative の中の False Positive の割合（FP / (FP + TN)）
  • 正直、下の ROC-AUC でしか使ったことがない
• ROC-AUC（Area Under the Receiver Operating Characteristic Curve）
  • 日本語だと「受信者動作特性曲線がなす面積」
  • 一般的に、分類モデルは各カテゴリに属する確率(0〜1の値）を出す
  • 通常は 0.5 を閾値にして、0.5未満なら属していない、0.5以上なら属していると判断する
  • この閾値を 0 から 1 まで変化させる
    • 閾値が 0 の時は「全部目的のカテゴリに属する」と予測するので、FN もTN も 0。すなわち True Positive Rate も False Positive Rate も １。
    • 閾値が 1 の時は「全部目的のカテゴリに属さない」と予測するので、TP も FP も 0。すなわち True Positive Rate も False Positive Rate も 0。
    • すなわち、閾値を 0 から 1 に変化させると、(False Positive Rate, True Positive Rate) は (1, 1) から (0, 0) までを動いていく
  • この時のｘ軸を False Positive Rate、ｙ軸を True Positive Rate とした曲線（ギザギザの線になるが）とｘ軸がなす面積が ROC-AUC（参考）
  • モデルが算出する確率の値まで評価した、モデル全体の性能を評価する値としてよく使われる
  • 閾値として 0.5 以外を使う場合に、どの値を閾値として使うのが良いかを見積もる場合にも使われる
    • 最も左上に膨らむ点である閾値を採用
  • imbalance にはそんなに強くない（TN を使っているから）
• MCC（Matthews Correlation Coefficient）（参考）
  • F1-score は Positive が極端に少ない imbalance には強いが、Positive が極端に多いimbalance には弱い
  • 
  • 混合行列の相関とも言える値で、混合行列に対して対称なので Positive が極端に多い imbalance にも強い

まだある。

今までの話は２クラス分類の場合の話であって、今回は９つの雑誌を当てる多クラス分類。だから上の指標は全部そのままでは使えない。
これらの２クラス分類の指標を多クラス分類に適用する方法は、大きく以下の３種類がある。

• micro
  • データそれぞれに TP, TN, FP, FN を計算し、それらをかき集めて指標を計算する
• macro
  • カテゴリ毎に「対象のクラスかそうでないか」（1-vs-rest）で指標を計算し、平均する
• weighted
  • macro の平均を取る時に、カテゴリ毎のデータ数を重みとした加重平均をとる

今回は F1-macro を使っている。みなさんがやる時には是非色々試して欲しい。

結果

で、やってみた結果だが、以下のようになった。

モデル	TRAIN	TEST
Support Vector Machine	0.8828	0.8219
Random Forest	0.9456	0.7445

Random Forest は明らかに過学習を起こしている。Cross Validation をしていてもこうなので、そもそもデータとモデルが合っていないということが考えられる。

Support Vector Machine は過学習を起こしていないし、F1 値が 0.8 ってなかなか優秀だ。

この時の混同行列を見てみると、毒女通信と Peachy、SMAX と IT Life Hack、家電チャンネルを間違えているものが多いことがわかる。これらは、前者はどちらも独身女性向け、後者はどちらもGeek向けなので、似たような単語を使っているために間違えたのかなと想像がつく。

まとめと参考文献

今回はNLP（文書分類）を Shallow Learning を用いて行った。

前処理として考える事・やる事が腐るほどあることが分かって頂けたかと思う。だから「AIの時代になっても人間の仕事はちっとも減らない」と私は考えている。手間を掛ければ掛けるほど良いものが出来る（可能性がある）のだ。（絶対に出来るとは言ってない）

また、大変だけど Shallow Learning でもそこそこの精度が出ることも分かって頂けたかと思う。なんでもかんでも Deep ではなく、Shallow を使ってデータの意味や構造、もしくはデータの裏に潜む真理なんてものを考えると良いんじゃないかと思う。

で、この記事は NLP が（一応）メインなので、Shallow Learning の説明はすっとばした。「機械学習を勉強するのに良い本はどれですか？」と聞かれることがしばしばあるのだが、やっぱりこれかな、と思う。

え？高い？英語で良ければ作者のページに PDF が