はじめに
レコメンドではALSという手法がしばしば使われるらしいが、あまり知らなかったので調べてまとめる。
なお、この記事は主に参考文献[1]の記事を参考にしてまとめたものである。
ALSの説明をするにはまずMatrix Factorizationについて説明する必要があるので、順を追って説明する。
レコメンドと強調フィルタリング
レコメンドではよく$k_{NN}$と強調フィルタリング (Collaborative Filtering) を組み合わせたものが用いられる。
強調フィルタリングとは雑に言えばAmazonとかでよくみる
「この商品を買った人はこんな商品も買ってますよ!」
というやつだ。
例えばスマブラを買ってる人がマリオカートもよく買う傾向があったとする。
このとき、スマブラを購入してるけどマリオカートは購入してない人がいたとすれば、
この人と似た属性の人がよく買っているマリオカートをお勧めすれば買ってくれる可能性が大きい。
こうやって強調フィルタリングでは「似た属性の人が何を好むか」に注目する。
そして、似た属性の人を探すのに$k_{NN}$と呼ばれる近傍探索がよく用いられる。
単純な強調フィルタリングの問題点
しかし、この$k_{NN}$ベースの強調フィルタリングには弱点がある。
その一つとして、大規模なデータだとスパース (=疎)になってしまうという問題がある。
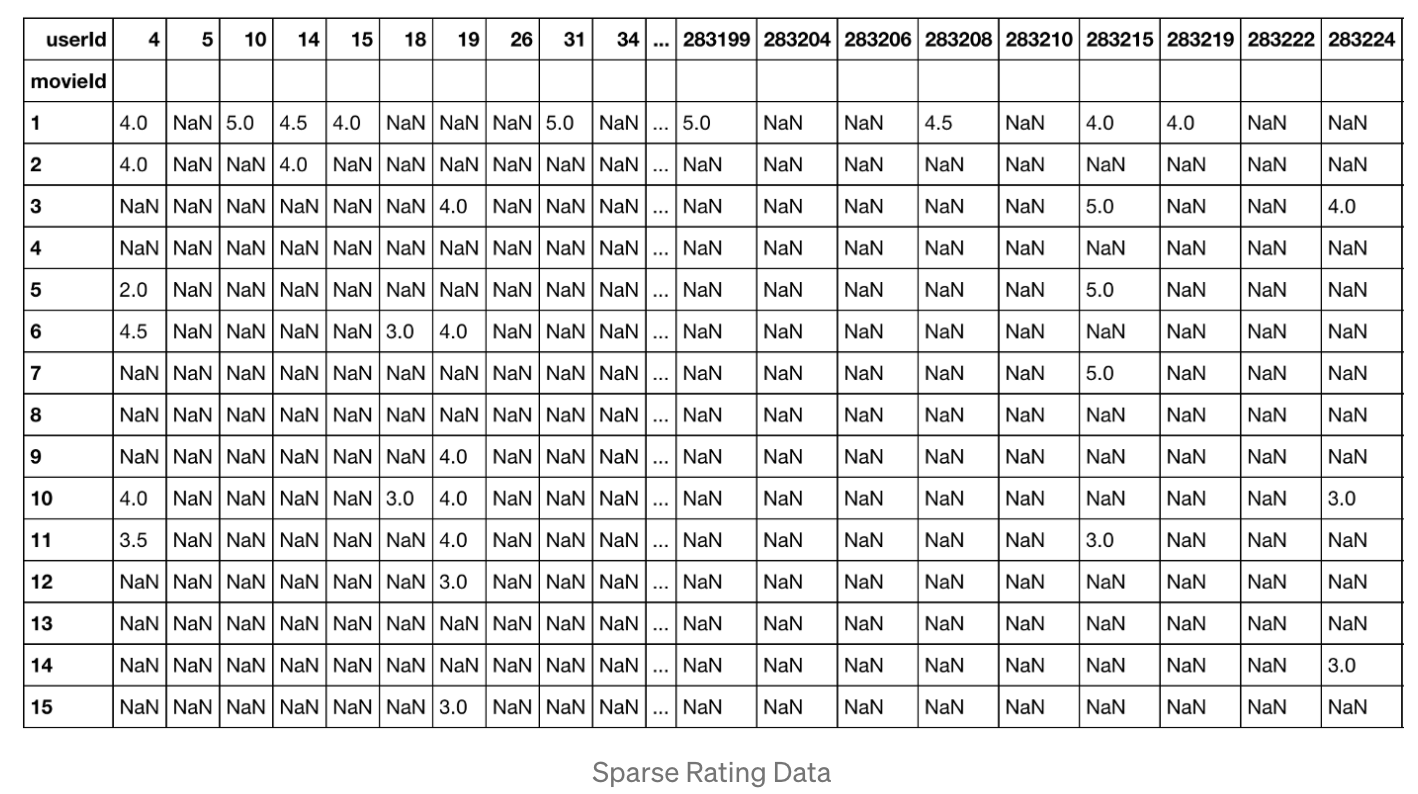
これはユーザーが映画につけたratingを表にしたものだ。
行が映画、列がユーザーを表している。
ユーザーの数も映画の数も膨大であるが、実際には一人のユーザーが見る映画の数なんて知れているので、ほとんどの項目はNaN (=評価不能)になる。
このスッカスカな状態をスパースと呼ぶ。
次元が増えすぎると計算が困難になるので、これを次元の呪い と呼んだりもする。
Matrix Factorizationを知る
次元を削減する方法で有名なものがMFだ。
この手法はNetflix Prizeと呼ばれるコンテストで一躍有名になったらしい。
[2]の説明がわかりやすかった。
商品の数m、ユーザー数nの組み合わせを考えるとする。
このとき、組み合わせの数はnmなので、ユーザー数、商品数が膨大になるほど組み合わせも膨れ上がる。
MFでは0<k<mとなるようなパラメータkを選び、nkの行列とk*mの行列に分解する。
すると要素は以下のように行列の内積で書けるようになる。[3]
w,hはそれぞれ商品、ユーザー行列を表す。

要素を計算するときには行列の積を計算することで値を埋めることになるので、空欄だった要素も予測値で埋めることができる。
k=2の場合はの図が以下([1])

ちなみにMFの登場以前は似たような次元削減の手法としてSVDが使われていたが、過学習になりやすいという弱点がある。
というのも、表の空欄部分は0 (=興味がない)ではなく評価不能であるべきだが、SVDを使うとこれを0としてnegativeに学習してしまうことが原因のようだ。
一方でMFの場合は実際にratingが付いている数値(=positive)な情報だけを使って次元削減を行っているため、このような問題は発生しない。
パラメータkは何を意味するのか
さて、このパラメータkとはは結局何なのか。
MFを使えばユーザーと商品はそれぞれk個の要素を持つベクトルとして表現されことになる。
これをembeddingと言ったりする。
ユーザーも商品もベクトルとして表現されているわけだから、コサイン類似度とかを計算すれば簡単に
ユーザー同士やユーザー×商品の類似度を計算するでき、とても便利。
ちなみに[1]の記事ではこのkのことをlatent factor (潜在的な要素)と呼んでいる。
内積計算するときにはkは足し合わせて消えちゃうので、あくまで潜在的というイメージかな。
MFにおける学習
MFにおいては要素を計算する時の行列の積ができるだけ真の値に近くなるように重みを学習する。
この辺りは一般的な機械学習の手法と同じで、過学習を防ぐために正則化項を加えたりする。
目的関数は以下の式になる。[1]

1項目が真のratingと予測したratingの差分で、2~3項目にあるのが正則化項である。
この手法はFunkさんが考えたのでFulk-SVDと呼ばれるらしい。
しかしこの手法では並列計算ができないという欠点がある。
この欠点を克服し、並列で計算できるようにしたのがALSである。
ALS (Alternating Least Squares) とは
ALS (Alternating Least Squares) はMF (Matrix Factorization)のアルゴリズムである。
Funk-SVDの欠点を克服し、並列で計算できるようにしたもの。
アルゴリズムは以下[1]

勾配降下法 (Gradient Decent)を使って重みを更新していく。
Funk-SVDと比べて以下の特徴がある
- L1正則化ではなくL2正則化を使う
- ユーザー行列と商品行列を交互に(Alternating)学習していく
- 片方を固定して片方の勾配を計算し...を繰り返す
交互に(Alternating)計算して最小二乗誤差を求めるので Alternating Least Squareと呼ぶわけだ。
このアルゴリズムは前述の通り並列計算が可能なのでSparkとかでぶん投げることができてとても便利。
以下にALSをsparkで回した時のサンプルnotebookがある。
https://github.com/KevinLiao159/MyDataSciencePortfolio/blob/master/movie_recommender/movie_recommendation_using_ALS.ipynb
ソースコードはもある
https://github.com/KevinLiao159/MyDataSciencePortfolio/blob/master/movie_recommender/src/als_recommender.py
ハイパーパラメータ
他の機械学習の手法と同じくハイパーパラメータのチューニングが必要。
validationもhold-outなりcross-validationなりつかってよしなにやる。
重要なパラメータとして以下がある。
- maxIter: iterationの最大値 (defaults: 10)
-
rank: latent factorsの数 (defaults: 10)
- 上記のMFの説明における
k
- 上記のMFの説明における
- regParam: 正則化パラメータ (defaults: 1.0)
確かにこの3つはどれも大事そう。
- iterationの数が増える -> 学習を進めることができるが、時間がかかる+過学習になりがち
- rankが増える -> user、itemをより高次のベクトル (embedding) で表現できるが、増えすぎると計算が複雑になる
- regParamが増える -> ペナルティを強くして過学習を抑制できるが、モデルの複雑さは減る
てところかな。
ライブラリの紹介
implicitというライブラリにALSがあるので、試してみる予定。
https://github.com/benfred/implicit
まとめ
- 強調フィルタリングやMFが導入されるまでの流れを説明した
- MFの一つであるALSの説明を行なった
- MFはいろんなところで導入されてるのでしっかり理解しておきたいね
参考文献
[1] https://towardsdatascience.com/prototyping-a-recommender-system-step-by-step-part-2-alternating-least-square-als-matrix-4a76c58714a1
この記事で一番参考にした記事
[2] https://qiita.com/ysekky/items/c81ff24da0390a74fc6c
QiitaのMFの説明記事
[3] https://arxiv.org/pdf/1205.2618.pdf
BPRの論文だがMFの説明が載ってる
[4] https://www.kaggle.com/code/julian3833/h-m-implicit-als-model-0-014
Kaggleのコンペ内でのALSの適用法