LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@tefuko

LSTM

Last updated at Posted at 2024-01-21

Sequence Models and Long-Short Term Memory Networks

シーケンスモデルとLSTMネットワーク

*A recurrent neural network is a network that maintains some kind of state.* リカレントニューラルネットワークとは、ある種の状態を維持するネットワークのことである。
*For example, its output could be used as part of the next input, so that information can propogate along as the network passes over the sequence.* たとえば、その出力を次の入力の一部として使用できるため、ネットワークがシーケンスを通過する際に情報を伝播できる。
*In the case of an LSTM, for each element in the sequence, there is a corresponding hidden state ht, which in principle can contain information from arbitrary points earlier in the sequence.* LSTMの場合、シーケンスの各要素にそれぞれ対応する隠れ状態$h_t$が存在し、原則として当該シーケンス以前の任意の時点からの情報を含むことができる。
*We can use the hidden state to predict words in a language model, part-of-speech tags, and a myriad of other things.* 隠れ状態を利用して、言語モデルの単語や品詞タグなどを予測することができる。

LSTM(Long-Short Term Memory) とは

*Hochreiter & Schmidhuber（1997）*により導入された、RNNのデメリットであった長期の時系列情報を考慮することで長期的な依存関係の学習を可能にしたRNNの派生モデル。
LSTMのメリットは長期間記憶を保持することで長期的な依存関係を考慮して回帰を実現できる点にある。

*図1 : LSTM*

LSTMの中間出力はRNNでも中間情報として出力されていた隱れ状態とLSTM特有のセル状態の2種類がある。

また、LSTMの特徴として忘却ゲート、入力ゲート、出力ゲートの3種類のゲートを持つという点がある。
ゲートとは、情報をどの程度次の時刻に伝達するかを制御するコンポーネントであり、$0$から$1$の値をとる。

  • コンポーネント … 部品、要素

LSTMのステップ

(1)
セル状態から捨てる情報を判定する。
この判定は忘却ゲート層と呼ばれるシグモイド層によって行われる。
$h_{t−1}$と$x_t$を見て、セル状態$C_{t−1}$の中の各数値のために$0$と$1$の間の数値を出力する。
この時、$1$は「完全に維持する」を表し、$0$は「完全に取り除く」を表す。

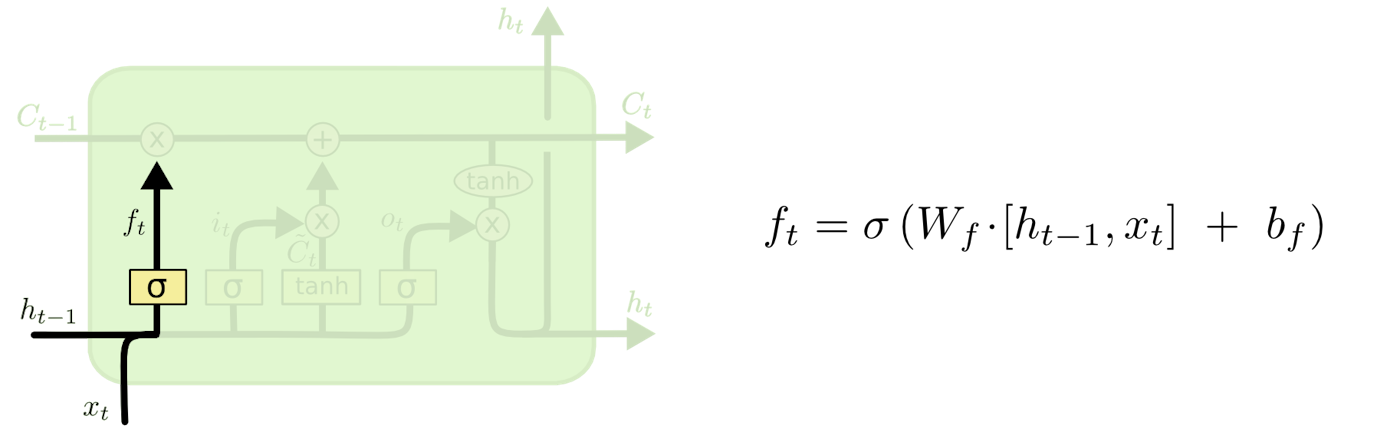
図2 : 忘却ゲート

  • ゲート … 選択的に情報を通す方法
  • シグモイド層 … $0$から$1$までの数値を出力し、コンポーネントをどの程度通すべきかを表す
    • $0$は「何も通さない」を、$1$は「全てを通す」を意味する

(2)
セル状態で保存する新たな情報を判定するために二つの層が用意されている。
入力ゲート層と呼ばれるシグモイド層ではどの値を更新するかを判定し、$tanh$層はセル状態に加えられる新たな候補値のベクトル$\tilde{C}_t$を作成する。
これら二つを組み合わせて状態を更新する。

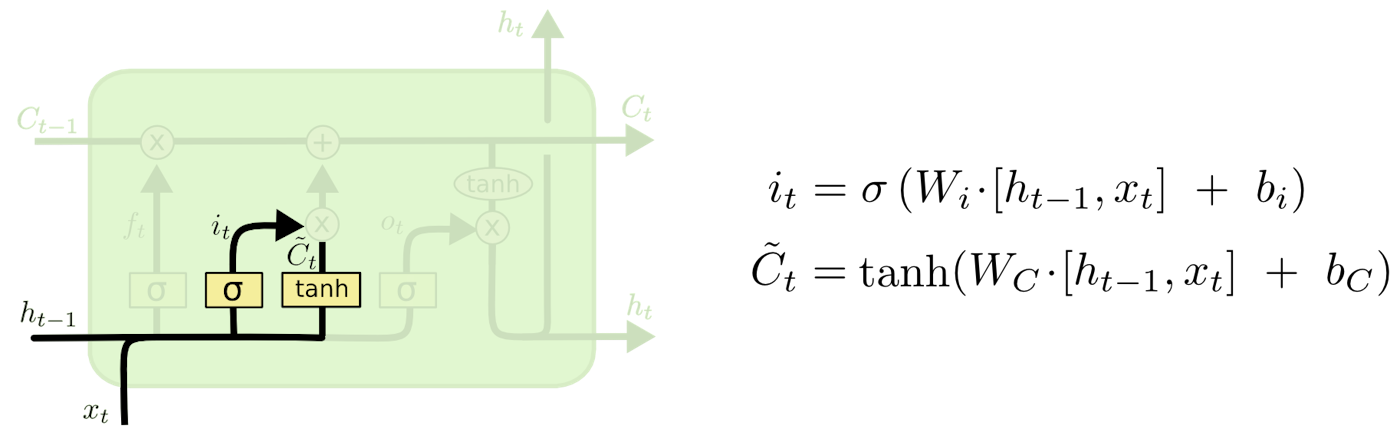
図3 : 入力ゲート層・$tanh$層

(3)
古いセル状態$C_{t-1}$から新しいセル状態$C_t$に更新する。

古いセル状態$C_{t-1}$に$f_t$を掛け、$(1)$で忘れると判定したものを忘れる。
次に、各状態値を更新すると決定した割合でスケーリングした新たな候補値 $i_t \ast \tilde{C}_t$ を加える。

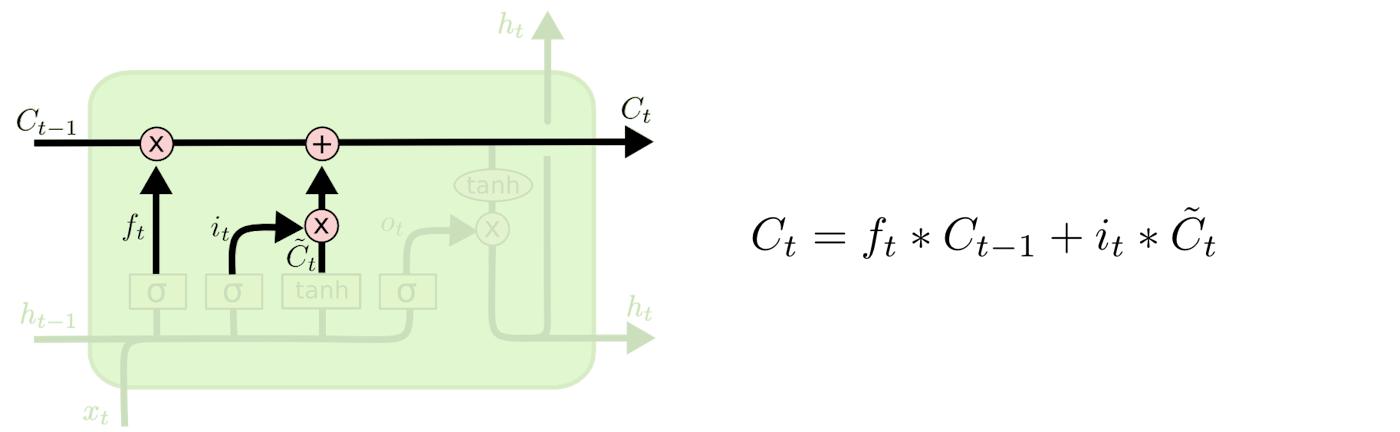
図4 … セル状態

  • スケーリング … ハードウェアや仮想マシンの負荷状況に応じて、通信ソフトウェアと仮想マシンを増減することにより処理能力を最適化する手続き
    • スケールアウト … 処理能力を向上させるために仮想マシンを追加する手続き
    • スケールイン … 処理能力を縮退させるために仮想マシンを削除する手続き

(4)
最後に出力するものを判定する。
この出力はセル状態をフィルタリングしたバージョンとなる。

まず、シグモイド層を実行し、セル状態のどの部分を出力するかを判定する。
その後、判定された部分のみを出力するため、セル状態に(値を$-1$と$1$の間に圧縮するために)$tanh$を適用し、それにシグモイド・ゲートの出力を掛ける。

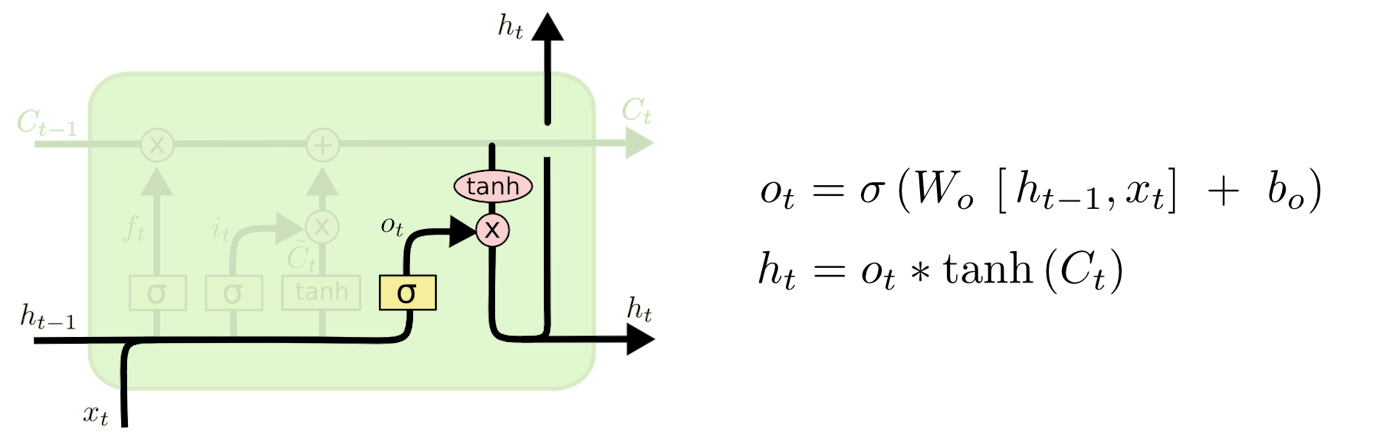
図5 … 出力

LSTMのバリエーション

  • 覗き穴の結合
    • ゲート層にセル状態を見せる

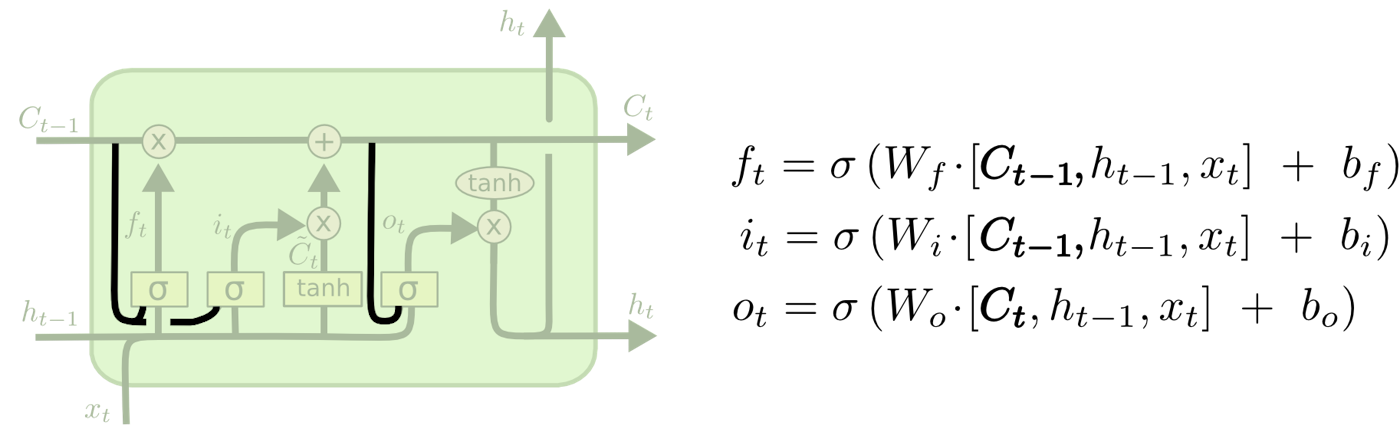
図6 … Gers & Schmidhuber (2000)ver.

図6では全てのゲートに覗き穴が追加されているが、多くの論文ではいくつかのゲートにのみ覗き穴を与えている。

  • 忘却ゲートと入力ゲートの組み合わせ
    • 何を忘れ、新しい情報を何に加えるべきかを別々に判定する代わりに、これらの判定を同時に行う
    • 該当箇所に何かを入力する時のみ忘却し、古いものを忘れた時のみ、状態に新しい値を入力する
*図7 … 忘却ゲートと入力ゲートの組み合わせ*
  • GRU(Gated Recurrent Unit)(Cho, et al.(2014))
    • 忘却ゲートと入力ゲートを単一の更新ゲートに組み合わせる
    • セル状態と隠れ状態をマージし、他にもいくつかの変更を加える
      • 結果として得られるモデルは標準的なLSTMモデルよりもシンプルで一般的になる
*図8 … GRU*

Pytorch における LSTM

*Pytorch’s LSTM expects all of its inputs to be 3D tensors.* PytorchのLSTMでは、すべての入力が3Dテンソルであると想定している。
*The semantics of the axes of these tensors is important.* これらのテンソルの軸の[意味論](https://ja.wikipedia.org/wiki/%E6%84%8F%E5%91%B3%E8%AB%96#%E3%82%B3%E3%83%B3%E3%83%94%E3%83%A5%E3%83%BC%E3%82%BF%E7%A7%91%E5%AD%A6)は重要である。
*The first axis is the sequence itself, the second indexes instances in the mini-batch, and the third indexes elements of the input.* 1つ目の軸はシーケンスそのものに、2つ目の軸はミニバッチのインスタンスに、3つ目の軸は入力の要素にインデックスを付ける。
*We haven’t discussed mini-batching, so lets just ignore that and assume we will always have just 1 dimension on the second axis.* ミニバッチについては説明していないため、それを無視して、第2軸には常に1つの次元があると仮定する。
*If we want to run the sequence model over the sentence “The cow jumped”, our input should look like* *The cow jumped* という文に対してシーケンスモデルを実行する場合、入力は以下のようになる。

$$
\begin{bmatrix}
\overbrace{q_{The}}^{列ベクトル} \
q_{cow} \
q_{jumped}
\end{bmatrix}
$$

*Except remember there is an additional 2nd dimension with size 1.* これはサイズ1の追加の2次元があることを除いている。
*In addition, you could go through the sequence one at a time, in which case the 1st axis will have size 1 also.* また、一度に1つずつ順番にシーケンスを実行することもでき、その場合は第1軸もサイズ1となる。
*Let’s see a quick example.* 簡単な例を示す。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)
# PyTorch のRNG(乱数ジェネレータ)を初期化

lstm = nn.LSTM(3, 3) 
# Input dim is 3, output dim is 3
    # 入力、出力は共に3次元

inputs = [torch.randn(1, 3) for _ in range(5)]
# torch.randn(1, 3) 正規分布における　1x3の乱数行列を生成
# make a sequence of length 5
    # 長さ5のシーケンスを作成する

# initialize the hidden state.
    # 隱れ状態を初期化する
hidden = (torch.randn(1, 1, 3),
          torch.randn(1, 1, 3))

for i in inputs:
    # Step through the sequence one element at a time.
        # 一度に1つずつ順番にシーケンスを実行する。
    # after each step, hidden contains the hidden state.
        # 各ステップの後、hiddenには隠れ状態が含まれている。
    out, hidden = lstm(i.view(1, 1, -1), hidden)

# alternatively, we can do the entire sequence all at once.
    # 代わりに、シーケンス全体を一度に実行することもできる。
# the first value returned by LSTM is all of the hidden states throughout
    # LSTMによって返される最初の値は
# the sequence. the second is just the most recent hidden state
    # 2番目は最新の隠れ状態
# (compare the last slice of "out" with "hidden" below, they are the same)
    # (最後の「out」と下の「hidden」を比較してみてみる)
# The reason for this is that:
    # その理由としては、以下のようなことが挙げられる。
# "out" will give you access to all hidden states in the sequence
    # "out" を実行すると、シーケンス内のすべての隠れ状態にアクセスできる。
# "hidden" will allow you to continue the sequence and backpropagate,
    # "hidden" を使用すると、シーケンスを継続して誤差逆伝搬することができ、
# by passing it as an argument  to the lstm at a later time
    # 後から lstm に引数として渡すことで
# Add the extra 2nd dimension
    # 2次元を追加する

inputs = torch.cat(inputs).view(len(inputs), 1, -1)
hidden = (torch.randn(1, 1, 3), torch.randn(1, 1, 3))
# clean out hidden state
    # 隱れ状態を整える

out, hidden = lstm(inputs, hidden)
print(out)
print(hidden)
Out
tensor([[[ 0.2486, -0.0525, -0.2524]],

        [[ 0.1750, -0.0048, -0.1143]],

        [[-0.0102,  0.0536, -0.1400]],

        [[-0.0357,  0.0877, -0.0192]],

        [[ 0.2145,  0.0192, -0.0337]]], grad_fn=<StackBackward>)
(tensor([[[ 0.2145,  0.0192, -0.0337]]], grad_fn=<StackBackward>), tensor([[[ 0.2984,  0.0952, -0.1647]]], grad_fn=<StackBackward>))

参考文献

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?