はじめに
GW中になにか一つアウトプットしたいと思ったので、自分が最初見たとき、ん?と思ったLSTMについて詳しく書いてみようと思います。
ところどころ数式も交えながら、なるべくわかりやすく書いていきたい所存です・・・!
シーケンスモデルの分類
本題に入る前にまず、シーケンス(系列データ)についてまとめます。
シーケンスモデルは以下の分類ができます。
-
one to one
入力データも出力データも固定サイズのベクトルである一般のニューラルネット。 -
one to many
入力データはシーケンスではないが、出力データはシーケンスである。
例として、画像キャプショニングがある。
画像キャプショニングでは、入力は画像であり、出力は英語のフレーズになる。 -
many to one
入力データはシーケンスだが、出力データは固定サイズのベクトルである。
例えば感情分析では、入力はテキストベースであり、出力はクラスラベルである。 -
many to many
入力データも出力データもどちらもシーケンスである。
これは入力と出力が同期するかに従って、さらに分類できる。- 遅延モデル:例として言語の翻訳がある。例えば英語を日本語に翻訳するときには、英語の文章全体を読み込んで処理した上で、日本語に翻訳しなければならない。
- 同期モデル:例として動画分類がある。動画分類では動画の各フレームがラベル付けされる。

参考URL: http://karpathy.github.io/2015/05/21/rnn-effectiveness/
RNN(Recurrent Neural Network)
LSTMを知るにはまず、RNNを理解しておく必要があります。
RNNとはなにか・・・
RNNは日本語では**「再帰型ニューラルネットワーク」**と呼ばれ、数値の時系列データなどのシーケンスデータのパターンを認識するように設計されたニューラルネットワークのモデルです。
例えば、多層パーセプロトロン(MLP)やCNNなどの標準のニューラルネットワークモデルでは、入力サンプルの順序を処理することはできません。
しかし、RNNは過去の情報を記憶しておき、その情報にしたがって新しい事象を処理することができます。
人間は、目の前で起きた出来事から、次に起こりそうな出来事を予測しながら文脈を読んで判断を下すことができます。例えば、車を運転している際に歩行者が飛び出しそうだと思えば、十分な間隔を置いて走行することが出来るでしょう。
それをニューラルネットで実現しようというのが、RNNの発想の原点になります。
RNNの構造
RNNは状態を扱う有向閉路を持つニューラルネットワークです。
この有向閉路をリカレントエッジと呼びます。
RNNは閉路上にコンテキスト(文脈)を持つ構造をしています。隠れ層が隠れ層自身に接続して、ある時点での状態を次の状態の入力値として使うことができます。

有効閉路が少し複雑に感じますが、下図のように、ループ構造を広げると考えやすいかもしれません。(数学でいう漸化式の展開)
柔軟に入力や出力数に応じて展開される長いニューラルネットワークのように見立てることができます。

参考URL: https://deepage.net/deep_learning/2017/05/23/recurrent-neural-networks.html
【参考】重み行列付きのより詳しい図だと以下(下記参考文献より引用させていただきましたm(__)m)

RNNの損失関数
RNNの学習アルゴリズムであるBPTT(Backpropagation Through Time)が紹介されたのは、1990年代にさかのぼります。
原著論文→http://www.cs.cmu.edu/~bhiksha/courses/deeplearning/Fall.2016/pdfs/Werbos.backprop.pdf
勾配の導出は少し複雑かもしれないですが、基本的には、全損失Lを時間$t=1$から$t=T$までのすべての損失関数の総和であると考えます。
$$
L = \sum_{t=1}^{T}L^{(t)}
$$
時間$t$までの損失は、それ以前のすべての時間刻みの隠れユニットに依存するため、勾配は次のように計算されます。
$$
\frac{\partial L^{(t)}}{\partial W_{hh}} = \frac{\partial L^{(t)}}{\partial y^{(t)}} \times \frac{\partial y^{(t)}}{\partial h^{(t)}} \times \left( \sum_{k=1}^{t}\frac{\partial h^{(t)}}{\partial h^{(k)}} \times \frac{\partial h^{(k)}}{\partial W_{hh}} \right)
$$
ここで、$\frac{\partial h^{(t)}}{\partial h^{(k)}}$は連続する時間刻みの総乗として計算されます。
$$
\frac{\partial h^{(t)}}{\partial h^{(k)}} = \prod_{i=k+1}^{t}\frac{\partial h^{(i)}}{\partial h^{(i-1)}}
$$
損失関数の勾配を計算するときの乗法係数$\frac{\partial h^{(t)}}{\partial h^{(k)}}$により、いわゆる勾配消失問題と勾配発散問題が発生してしまいます。
これを解決するために登場したのがLSTMです。
(How LSTM networks solve the problem of vanishing gradients ← この記事めちゃ参考になります!(いつか翻訳したい))
RNNからLSTMへ
LSTM(Long Short-Term Memory)は勾配消失問題を解決する方法として1997年に提唱されたものです。
LSTMはRNNの中間層のユニットをLSTM Blockと呼ばれるメモリと3つのゲートを持つブロックに置き換えることで実現されています。
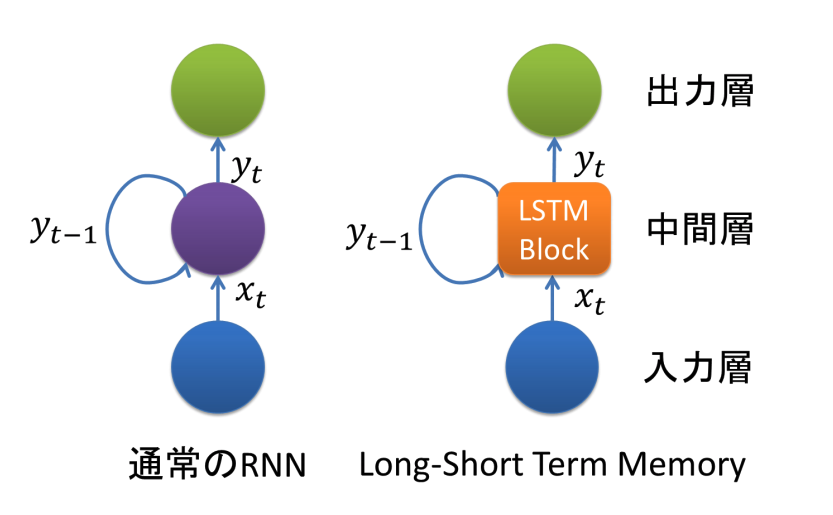
参考URL: https://qiita.com/t_Signull/items/21b82be280b46f467d1b
通常のRNNでも数十ステップの短期依存(short-term dependencies)には対応できるのですが、1000ステップのような長期の系列は学習することができませんでした。
LSTMはこのような系列に対しても適切な出力を行うことができます。
LSTM Blockの中身を探る
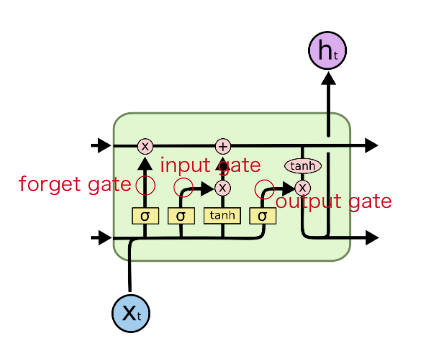
LSTMの画期的な特徴は、「ゲート」と呼ばれる情報の取捨選択機構を持った点です。
ゲートは選択的に情報を通す方法です。
ゲートには以下の3種類があります。
- Input gate: 入力を取り込むか選ぶ
- Forget gate: cellに保持している情報をリセットするか選ぶ
- Output gate: 次の時刻にどの程度情報を伝えるか選ぶ
それぞれ詳しく見てみましょう。
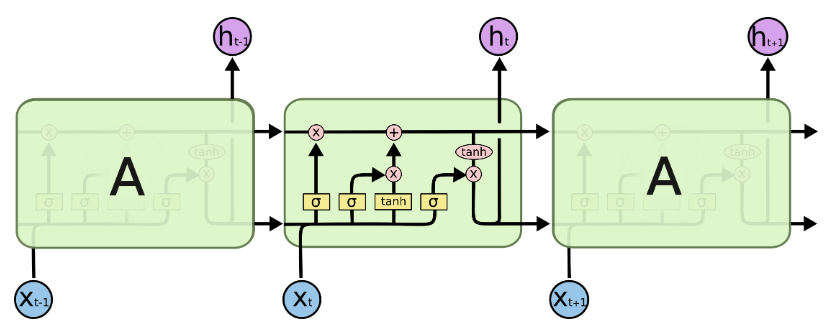
参考URL: http://colah.github.io/posts/2015-08-Understanding-LSTMs/
シグモイド層は0から1までの数値を出力します。
この数値は各コンポーネントをどの程度通すべきかを表します。0は「何も通さない」を、1は「全てを通す」を意味します。
input gateは、セル状態を更新する役割を果たします。
forget gateでは、通過させる情報と通化させない情報を決定します。
output gateは、隠れユニットの値の更新方法を決定します。
LSTMでsin波を予測してみる
RNN, LSTMの概要がわかったところで、チュートリアルとして、よくあるsin波の予測をやってみようと思います。
データ生成
ノイズのあるsin波のデータを作成します。
import pandas as pd
import numpy as np
import math
import random
import matplotlib.pyplot as plt
import seaborn as sns
# サイクルあたりのステップ数
steps_per_cycle = 80
# 生成するサイクル数
number_of_cycles = 50
df = pd.DataFrame(np.arange(steps_per_cycle * number_of_cycles + 1), columns=["t"])
# 一様乱数でノイズを発生させたsin波を生成
df["sin_t"] = df.t.apply(lambda x: math.sin(x * (2 * math.pi / steps_per_cycle)+ random.uniform(-0.05, +0.05) ))
# 2サイクルだけ抽出してプロット
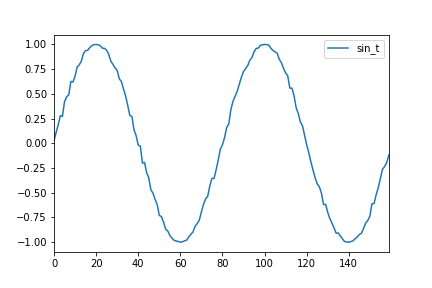
df[["sin_t"]].head(steps_per_cycle * 2).plot()
# 画像を保存
plt.savefig('img_20190505085043.png')
以下のようなグラフができたら成功です。
続いて、これを訓練データ、テストデータに分類します。
今回は30ステップ分の入力Xがあった際の出力yが31ステップ目になる様なデータセットを作ります。
def _load_data(data, n_prev=30):
docX, docY = [], []
for i in range(len(data) - n_prev):
docX.append(data.iloc[i:i + n_prev].values)
docY.append(data.iloc[i + n_prev].values)
alsX = np.array(docX)
alsY = np.array(docY)
return alsX, alsY
def train_test_split(df, test_size=0.1, n_prev=30):
ntrn = round(len(df) * (1 - test_size))
ntrn = int(ntrn)
X_train, y_train = _load_data(df.iloc[0:ntrn], n_prev)
X_test, y_test = _load_data(df.iloc[ntrn:], n_prev)
return (X_train, y_train), (X_test, y_test)
ここでは、分け方が変則的なのでscikit-learnのtrain_test_split関数は使えず、自分で定義する必要があることに注意が必要です。
定義したtrain_test_splitを使い、train dataとtest dataに分割します。
(X_train, y_train), (X_test, y_test) = train_test_split(df[["sin_t"]])
モデルの生成
今回はkerasを使ってモデルを生成し、学習させます。
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import LSTM
# パラメータ
in_out_neurons = 1
hidden_neurons = 300
length_of_sequences = 30
model = Sequential()
model.add(LSTM(hidden_neurons, batch_input_shape=(None, length_of_sequences, in_out_neurons), return_sequences=False))
model.add(Dense(in_out_neurons))
model.add(Activation("linear"))
model.compile(loss="mean_squared_error", optimizer="rmsprop")
model.fit(X_train, y_train, batch_size=600, nb_epoch=15, validation_split=0.05)
- n_hidden: 隠れ層
- 回帰問題なので、線形の活性化関数と損失関数にMSEを用いている
予測データを図示してみて、sin波が再現できるか確認してみます。
# 予測
predicted = model.predict(X_test)
# 描写
dataf = pd.DataFrame(predicted[:200])
dataf.columns = ["predict"]
dataf["input"] = y_test[:200]
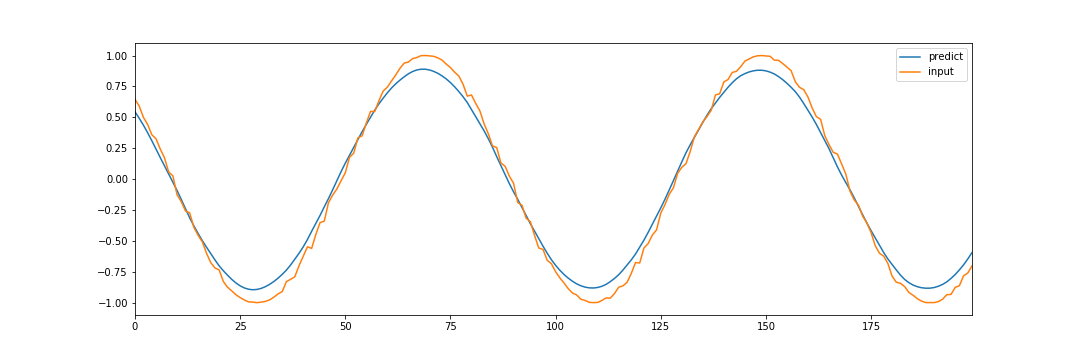
dataf.plot()
オレンジが元データで、青が予測されたデータです。
少し振幅が小さいようですが、おおよそうまく予測することができています。
おわりに
シーケンスモデルの分類から、RNNの紹介、LSTMの生まれた経緯&概要、そしてkerasを使っての実装までをやってみました。
なにかの参考になれば幸いです。
参考サイト
- http://karpathy.github.io/2015/05/21/rnn-effectiveness/
- https://deepage.net/deep_learning/2017/05/23/recurrent-neural-networks.html
- https://qiita.com/t_Signull/items/21b82be280b46f467d1b
- http://colah.github.io/posts/2015-08-Understanding-LSTMs/
- https://medium.com/datadriveninvestor/how-do-lstm-networks-solve-the-problem-of-vanishing-gradients-a6784971a577