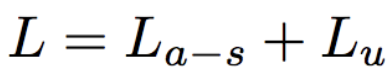Softmax関数をベースにした Deep Metric Learning が上手くいく理由

はじめに

　Deep Learningを使った距離学習（Metric Learning）では、Contrastive LossやTriplet Lossなどを用いて、画像間の類似性（や非類似性）を直接学習していく方法が広く利用されていますが、学習データの組み合わせや選び方が難しく、学習自体が難航するケースが多い事も知られています。それだけに、これまで様々な改良と工夫が提案されています。
　しかし、最近はこのような学習データ選びに難航することなく、一般的なクラス分類タスクの感覚で、Softmax関数をベースに学習できるMetric Learningが注目を浴びています。ArcFaceなどはその代表的手法でこちらで詳しく説明されています。
　Softmax関数をベースにしたMetric Learningがうまくいく理由、またさらなる改良の余地はあるのか？これらに関して少し紹介しようと思います。

Center Loss

　クラス分類にMetric Learningの要素を取り入れた元祖といえばCenter Loss¹ではないでしょうか。Center Lossに関しては、こちらで詳細に説明されていたので、ざっと要点のみを紹介します。
　Center Lossでは、各特徴ベクトルと対応するクラス中心との距離にペナルティを設けることで、クラス分類と特徴空間上のクラス中心位置を同時に学習します。これによりクラス内変動は小さくなるため、より効果的にクラス分離する方法としてECCV2016で発表されました。

　本論文では、CNNの最終層の１つ手前のFC層を２次元に改良し、その値をそのまま２次元平面にプロットする事で特徴量の可視化を行っています。下図はMNISTに対して通常のSoftmax関数でクラス分類した際の中間特徴量を可視化したものです。

　損失関数は、通常のSoftmax Cross Entropy Lossに、各特徴ベクトルとそのクラスの中心ベクトルとの距離を表すCenter Lossの項を加えたものになります。

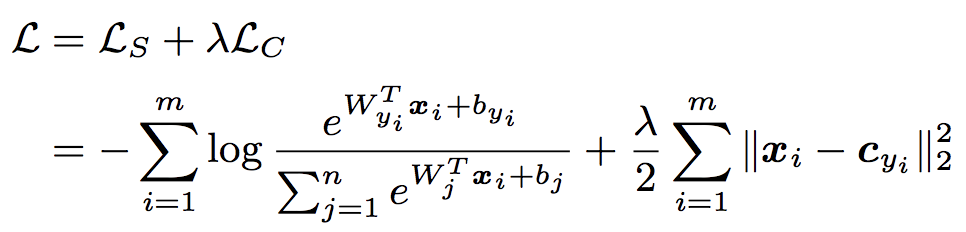
クラスの中心$C_{y_i}$を都度正確に計算するのは計算量的に現実的ではないため、ミニバッチ毎に以下の計算を行い、クラス中心$C_{y_i}$を逐次更新していきます。

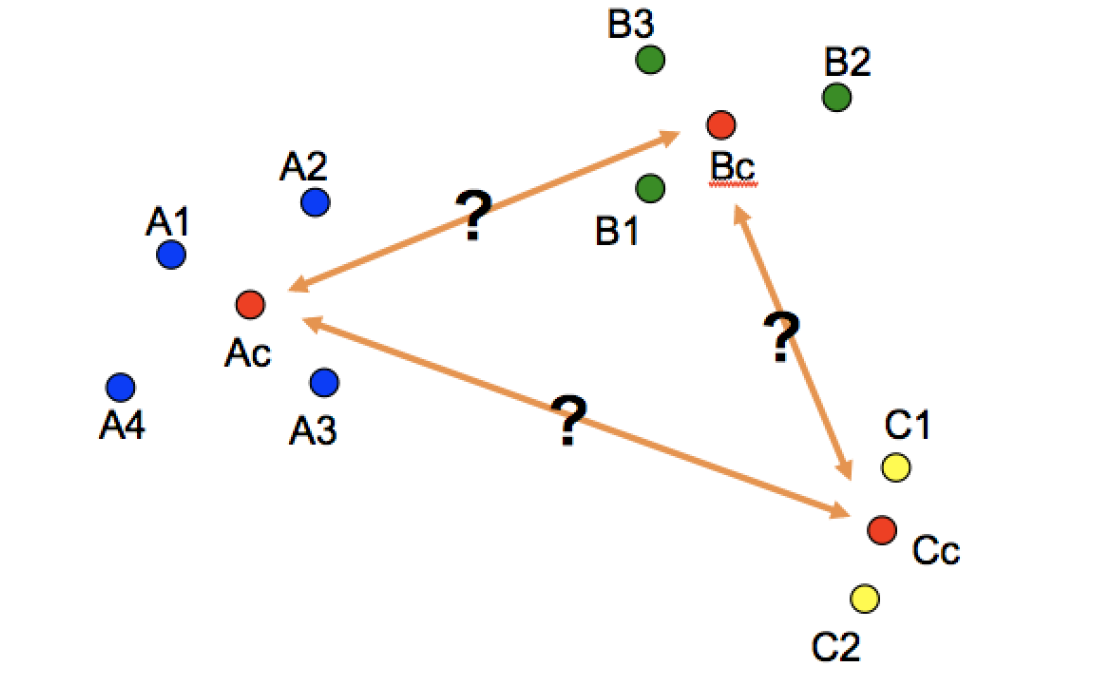
以下はクラス中心の具体的な更新例です。ミニバッチ内でクラスAに属するデータが$A1$、$A2$、$A3$の３つの場合、クラスAの中心位置$C_A$は下図のように更新されます。

　最後に Center Lossの結果を可視化した図を載せておきます。ハイパーパラメータ$\lambda$の値を大きくする事で、クラス内変動も小さくなることが分かります。

Sphereface

　Softmax関数を使って学習した場合の特徴空間には固有の角度分布がある事を見出し、Center Lossのようなユークリッド距離によるマージンよりも、角度に基づくマージンの方が適しているという事を主張。Angular Softmax (A-Softmax) Lossを提案²し、CVPR2017で採択されました。

　順に見ていきたいと思います。まず、通常のSoftmax Cross Entropy Lossは以下の通りです。

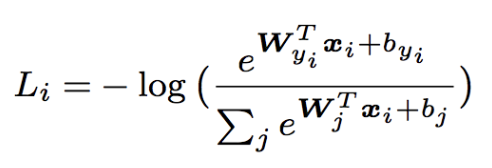
次に、これを内積の公式 $\boldsymbol{a}\cdot\boldsymbol{b}=||\boldsymbol{a}||\,||\boldsymbol{b}||\cos\theta$ を使って $\boldsymbol{W^T_j}$と$\boldsymbol{x_i}$の内積部分を書き換えます。

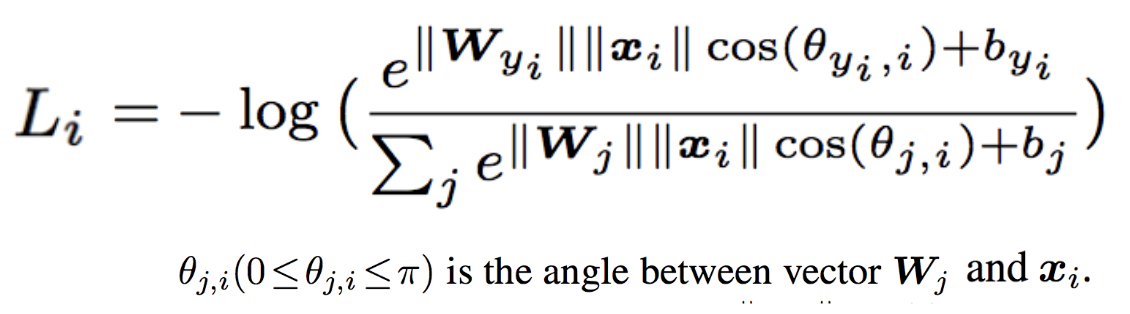
さらに、重みパラーメタを正規化して$||\boldsymbol{W_j}|| = 1$となるようにし、バイアス$b_j$も$0$にします。
すると、以下のようになり、これをModified Softmax Lossと定義します。

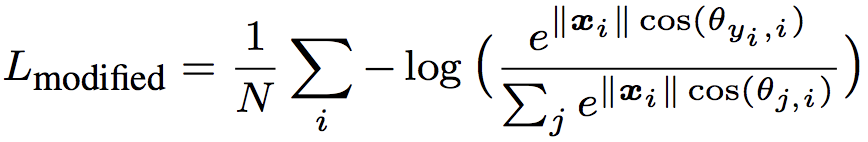
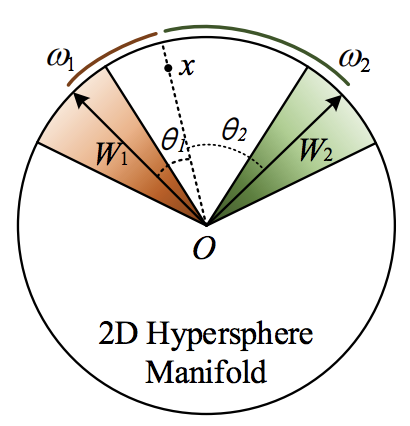
次に、この$L_{modified}$における決定境界がどうなっているのか確かめてみます。決定境界とは２つのクラスがちょうど同じ確率になる境界値を指します。

クラス１の重み$W_1$と特徴量$x_i$のなす角を$\cos\theta_1$、クラス２の重み$W_2$と特徴量$x_i$のなす角を$\cos\theta_2$とすると、この２つの確率がちょうど同じになるのは以下の条件を満たす場合です。

\frac{e^{\|\boldsymbol{x_i}\|\cos\theta_1}}{\sum_{j} e^{\|\boldsymbol{x_i}\|\cos(\theta_{j,i})}} = \frac{e^{\|\boldsymbol{x_i}\|\cos\theta_2}}{\sum_{j} e^{\|\boldsymbol{x_i}\|\cos(\theta_{j,i})}} \\
\|\boldsymbol{x_i}\|\cos\theta_1 = \|\boldsymbol{x_i}\|\cos\theta_2 \\
\theta_1 = \theta_2

したがって、クラス1とクラス2の確率がちょうど同じになるのは、重み$W_1$と$W_2$の角度を２等分する直線方向に$x_i$がある場合です。

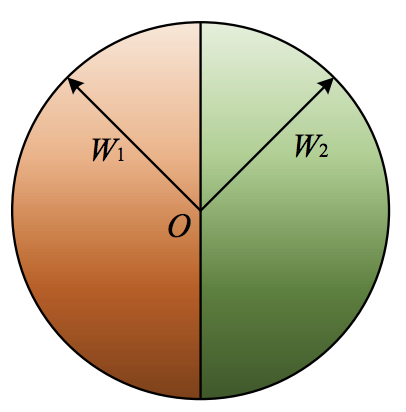
この結果から、Softmax Lossによって学習された特徴量$x_i$というのは、本質的にはsoftmaxをかける直前の最後の重み$Wj$の角度に沿った分布をとっていることがわかります。

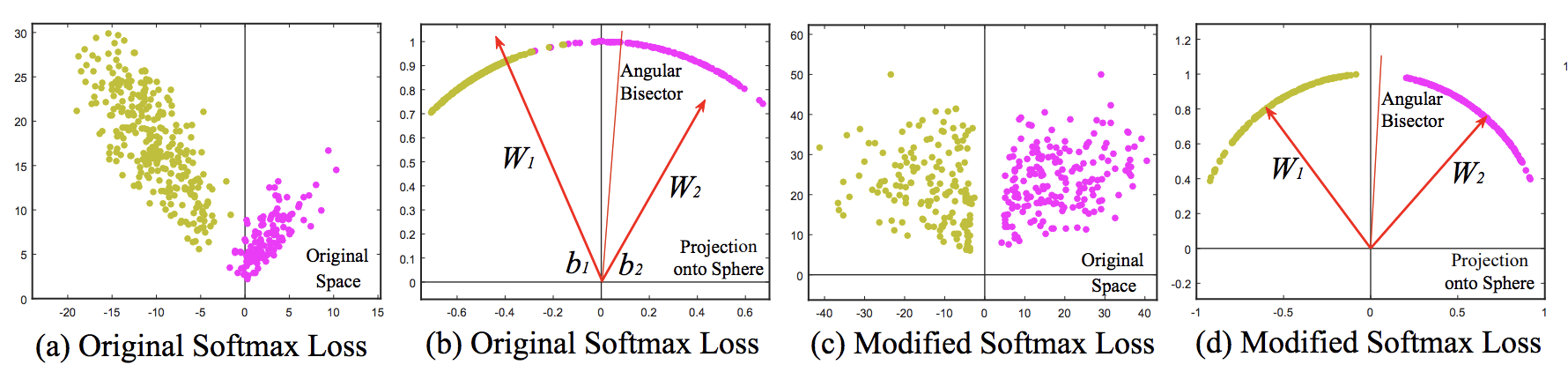
これはつまり、Softmax関数に対して、Center Lossのようにユークリッド距離ベースのマージンを組み合わせるのは親和性がよくない事を示唆しており、角度に沿ったマージンを設ける事こそが最も効果的であると示しています。

Angular Softmax (A-Softmax) Loss

Angular Softmax (A-Softmax) Lossは以下のように定義されています。

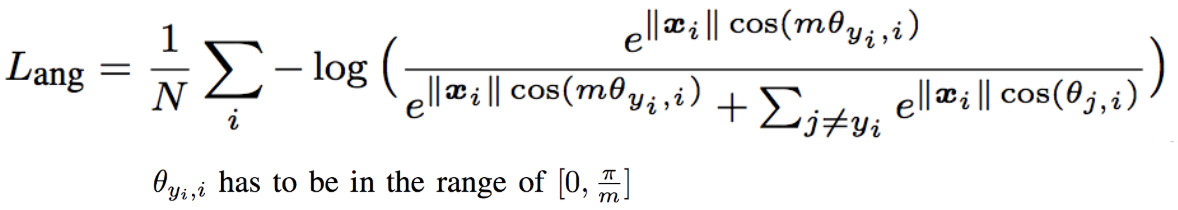
$L_{modified}$に対して、自クラスの重み$W_{y_i}$とのなす角$\theta_{y_i,i}$にのみ係数$m$のペナルティを与えるため、決定境界を本来の位置よりも自クラスの重み$W_{y_i}$のに近くに寄せる効果が期待あります。

CosFaceやArcFace

　Spherefaceが主張するような角度に沿ったマージンをとるやり方は、Sphereface以降にもいくつか提案されています。CosFace³やArcFace⁴などがそれにあたります。

　詳細な内容は割愛しますが、簡単に説明すると、CosFaceからは$x_i$の正規化も行われるようになったため、２つのベクトルのなす角の$\cos\theta$がそのまま類似度として表現できるようになりました。また、$\cos\theta$の値が小さすぎてSoftmaxが機能しなくなるのを防ぐためにハイパーパラメータ$s$を導入しています。
　さらにその後、ArcFaceはマージンの場所を変更しています。角度に直接マージン指定しているので、Softmaxにおける分離境界は区間全体に渡って線形かつ一定となります。

Uniform Loss

　SpherefaceなどのCosine Based Softmax LossにUniform Lossという新しい項を追加する事で、クラス中心を均一に分散させる等分布制約を課し、特徴空間を最大限に活用できるようにする手法が提案⁵されました。CVPR2019で採択されています。Uniform Lossは、特徴空間である超球面上で、クラスの中心をクラス間反発を伴う電荷のように考え、そのポテンシャルエネルギーを最小化するような働きをします。これまでの既存手法は、クラス間距離を大きくすることとクラス内変動を小さくすることを目標にしているものが多いですが、Uniform Lossではそれに加えてクラス間距離の最小値の最大化も期待できます。

　Center Loss の場合は、クラス内の要素とクラス中心との間の距離を単に最小化するのみで、そもそもクラス間の関係は記述されていません。

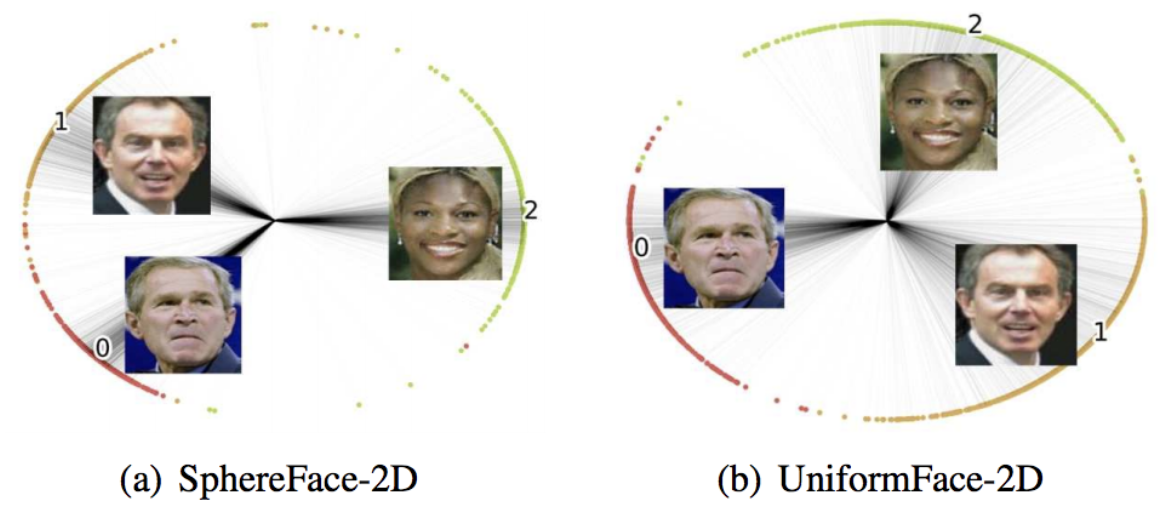
　Sphereface、Cosface、Arcface の場合は、超球面上でマージンを持った識別境界が学習されるので、結果的にクラス内変動は小さく、クラス間距離は大きくなるように学習が進みます。ただし、特徴空間の全体的な分布を明示的に制約しているものはないため、特徴空間内で局所的な配置となり、バランスが取れていない可能性があります。

　Uniform Lossは、球の表面上に電荷を配置した場合、それらが均一に分布した場合にポテンシャルエネルギーが最小化されるという事実がモチベーションとなっているので、クラスの中心を電荷とみなし、その電位エネルギーを表す関数をLossとして表現します。

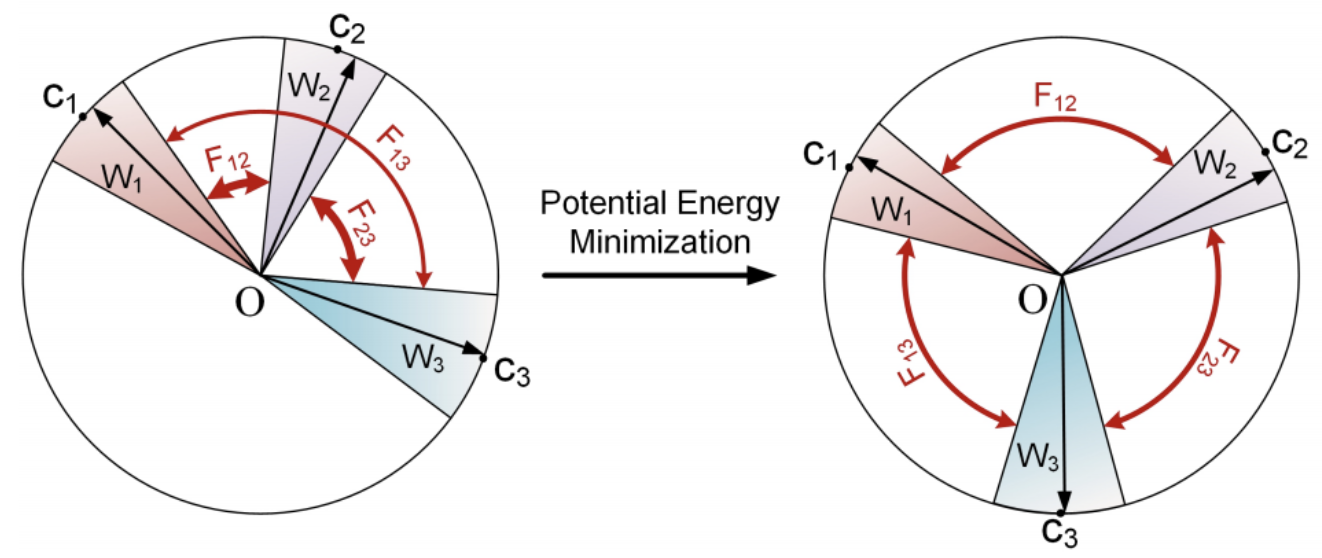
２つのクラス間にその距離の２乗に反比例する反発力$F$を定義します。

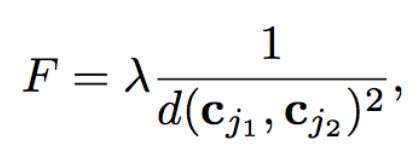
距離関数$d$ は、クーロンの法則をそのまま踏襲しユークリッド距離を使用します。また、反発力$F$が大きくなりすぎるのを防ぐために1を加えます。

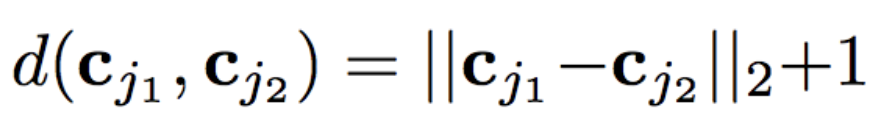
全てのクラス中心のペアワイズのエネルギーの平均値としてUniform Lossを定式化します。

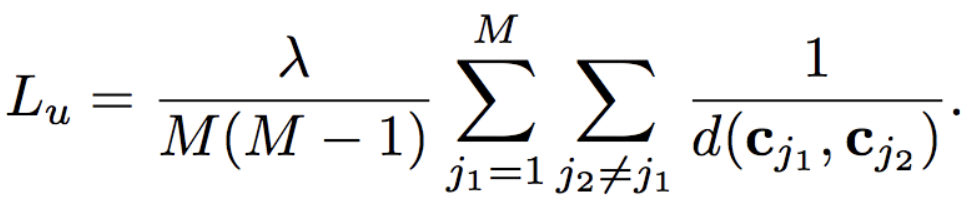
SpherefaceのLoss（Cosine Based Softmax Loss）関数の部分は以下の通りです。

この２つのLossの和が最終的なLoss関数となります。

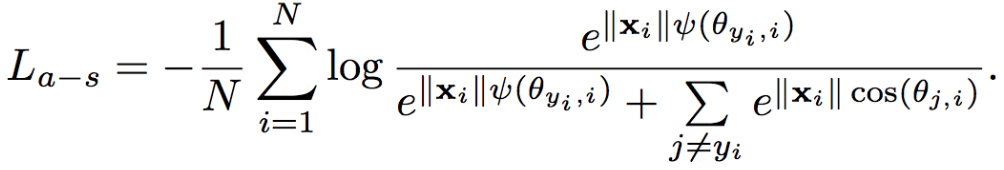
最後に、クラスの中心の更新方法ですが、これはCenter Lossのそれと全く同じ方法で更新します。

ちなみに余談になりますが、3次元球面上にN個の点を置き、点間の球面距離の最小値が最大となるように配置した場合、その球面距離の長さはいくつになるか？という問題はTammes問題と呼ばれていて、現在でも完全な解答が見つかっていない数学上の未解決問題の一つだそうです。

P2SGrad

　SenseTime ResearchとThe Chinese University of Hong Kongの共同研究として、AdaCos⁶とP2SGrad⁷という２つの論文が2019年5月7日に同じAuthorから同時に発表されました。どちらの論文もCVPR2019で採択（AdaCosの方はOral採択）されています。提案されている手法もさることながら、Sphereface、Cosface、ArcfaceなどのCosine Based Softmax Lossの本質的な違いや、勾配の最適化のプロセスに関して言及している点が特に面白いと感じました。AdaCosに関しては既にこちらで説明されていたので、P2SGradの方を詳しくみていきたいと思います。

　さて、P2SGradですが、特筆すべきは、特定の損失関数を定式化せずに、モデルを最適化できる点だと思います。Metric Learningに関わらず、一般的なDeep Learningでは損失関数を定義し、損失関数が小さくなるように重みやバイアスを更新しながら学習していくというのが定石です。しかし、P2SGradでは、特徴空間の重みベクトルを更新するための最適な勾配方向と大きさを直接的に求め、それをBackpropagationしてパラメータの最適化を進めていきます。さらに、損失関数を定義しなくてよいということは、ArcFaceやCosFaceの損失関数にあった$m$や$s$といったハイパーパラメータを調整する必要もありません。

Cosine Based Softmax Loss の Backpropagation

まずは、角度マージンのない Cosine Based Softmax Lossに関する勾配を確認しておきます。
次の $f_{i,j}$は 特徴量$\vec{x_i}$のクラス$j$ に関する logits になります。

f_{i,j}  = s \cdot \frac{\langle \vec{x_i}, \vec{W_j} \rangle}{\|\vec{x_i}\|_2\|\vec{W_j}\|_2} = s \cdot \langle \boldsymbol{\hat{x_i}}, \boldsymbol{\hat{W_j}} \rangle = s \cdot \cos\theta_{i,j} \tag{1}

$\boldsymbol{\hat{x_i}}$と$\boldsymbol{\hat{W_j}}$はそれぞれ$\vec{x_i}$と$\vec{W_j}$の正規化されたベクトルを表します。

クラス数が$C$の場合、$i$ 番目の特徴量がクラス $j$である確率$P_{i,j}$は、Softmax関数で下記のように書けます。

P_{i,j} = Softmax(f_{i,j}) = \frac{e^{f_{i,j}}}{\sum^{C}_{k=1}e^{f_{i,k}}} \tag{2}

正解クラスが$y_i$の場合のCross Entropy Lossは次のようになります。

L_{CE}(\vec{x_i}) =-\log{P_{i, y_i}} = -\log{\frac{e^{f_{i,y_i}}}{\sum^{C}_{k=1}e^{f_{i,k}}}} \tag{3}

この $L_{CE}(\vec{x_i})$ に対し、$\vec{x_i}$ と $\vec{W_j}$ の勾配を求めます。

\frac{\partial L_{CE}(\vec{x_i})}{\partial \vec{x_i}} = \sum_{j=1}^{C}(P_{i,j} - \mathbb{1}(y_i=j)) \nabla f(\cos\theta_{i,j}) \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{x_i}} \tag{4}

\frac{\partial L_{CE}(\vec{x_i})}{\partial \vec{W_j}} = (P_{i,j} - \mathbb{1}(y_i=j)) \nabla f(\cos\theta_{i,j}) \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} \tag{5}

関数 $\mathbb{1}(y_i=j)$ は、$j=y_i$のとき$1$で、それ以外は$0$になります。
さらに $\frac{\partial \cos\theta_{i,j}}{\partial \vec{x_i}}$ と $\frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}}$ を計算すると、それぞれ以下のようなベクトル値になります。

\frac{\partial \cos\theta_{i,j}}{\partial \vec{x_i}} = \frac{1}{\|\vec{x_i}\|_2}(\boldsymbol{\hat{W_j}} - \cos\theta_{i,j} \cdot \boldsymbol{\hat{x_i}}) \tag{6}

\frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} = \frac{1}{\|\vec{W_j}\|_2}(\boldsymbol{\hat{x_i}} - \cos\theta_{i,j} \cdot \boldsymbol{\hat{W_j}}) \tag{7}

次に、$\nabla f(\cos\theta_{i,j})$の部分を計算します。$f$は logits 部分を表す関数なので、角度マージンを持たない$f(\cos\theta_{i,j})$は$s \cdot \cos\theta_{i,j}$です。したがって $\nabla f(\cos\theta_{i,j}) = s$ となります。
Cosfaceの場合は$f(\cos\theta_{i,y_i})=s \cdot (\cos\theta_{i,y_i} - m)$なので$\nabla f(\cos\theta_{i,y_i}) = s$となり、Arcfaceの場合は$f(\cos\theta_{i,y_i})=s \cdot \cos(\theta_{i,y_i} + m)$なので、$\nabla f(\cos\theta_{i,y_i}) = s \cdot \frac{\sin(\theta_{i,y_i} + m)}{\sin\theta_{i,y_i}}$となります。

いずれにしても、$\nabla f(\cos\theta_{i,j})$はパラメータ$s$や$m$や$\cos\theta_{i,y_i}$によって決まるスカラー値になります。また、普通は$s>1$の値を使うので、上記は全て$\nabla f(\cos\theta_{i,j}) > 1$となります。

それでは改めて、$\frac{\partial L_{CE}(\vec{x_i})}{\partial \vec{W_j}}$を$j$によって場合分けして整理してみましょう。

$j \neq y_i$の場合

\frac{\partial L_{CE}(\vec{x_i})}{\partial \vec{W_j}} = P_{i,j} \cdot \nabla f(\cos\theta_{i,j}) \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} = T \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} \tag{8}

$j = y_i$の場合

\frac{\partial L_{CE}(\vec{x_i})}{\partial \vec{W_j}} = (P_{i,j} - 1) \cdot \nabla f(\cos\theta_{i,j}) \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} = U \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} \tag{9}

$P_{i,j}$はSoftmaxの値なので、取り得る値の範囲は $P_{i,j} \in [0, 1]$ です。つまり、上式の$T$および$U$はそれぞれ$T>0$と$U<0$ の範囲をとるスカラー値ということになります。

Backpropagationによって重みベクトル$\vec{W_j}$は、下記のように最適化されていきます。

\vec{W_j} \leftarrow \vec{W_j} - \eta\cdot \frac{\partial L_{CE}}{\partial \vec{W_j}} \tag{10}

これらの事実にもとづいてまとめると、以下の事がわかります。

• 正解クラスの重みパラメータ$\vec{W_{y_i}}$は、Backpropagationによって$\vec{W_{y_i}}$に垂直な$\frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}}$ の方向に更新されていく。そしてその勾配ベクトルの長さは$(P_{i,j} - \mathbb{1}(y_i=j)) \nabla f(\cos\theta_{i,j})$である。

• 正解じゃないクラスの重みパラメータ$\vec{W_j}$は、Backpropagationによって$\vec{W_j}$に垂直な $-\frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}}$の方向に更新されていく。そしてその勾配ベクトルの長さは$(P_{i,j} - \mathbb{1}(y_i=j)) \nabla f(\cos\theta_{i,j})$である。

• $\frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}}$は、$\vec{W_j}$に対して垂直方向なので、これは最速かつ最適でとても合理的な更新である。

• Cosine Based Softmax Lossは、CosFaceやArcFaceなどいろいろあるが、更新する勾配方向は全て同じである。これらの本質的な違いは勾配の長さ部分であり、この部分がモデルの最適化に大きく影響している。

勾配の長さ

　これまでみてきたように、勾配の長さは $(P_{i,j} - \mathbb{1}(y_i=j)) \cdot \nabla f(\cos\theta_{i,j})$なので、$P_{i,j}$の値が勾配の長さに大きく影響します。さらに、$P_{i,j}$は logits $f_{i,j}$と正の相関があります。そして、logits $f_{i,j}$はハイパーパラメータ$s$や$m$の影響を強く受けます。

　ArcFaceの例をみていきます。$f_{i,y_i}$ は $s \cdot \cos(\theta_{i,y_i} + m)$です。ハイパーパラメータ$s$と$m$が異なると同じ$\theta_{i,y_i}$の場合でも、$P_{i,y_i}$の値が大きく変わる事がわかります。

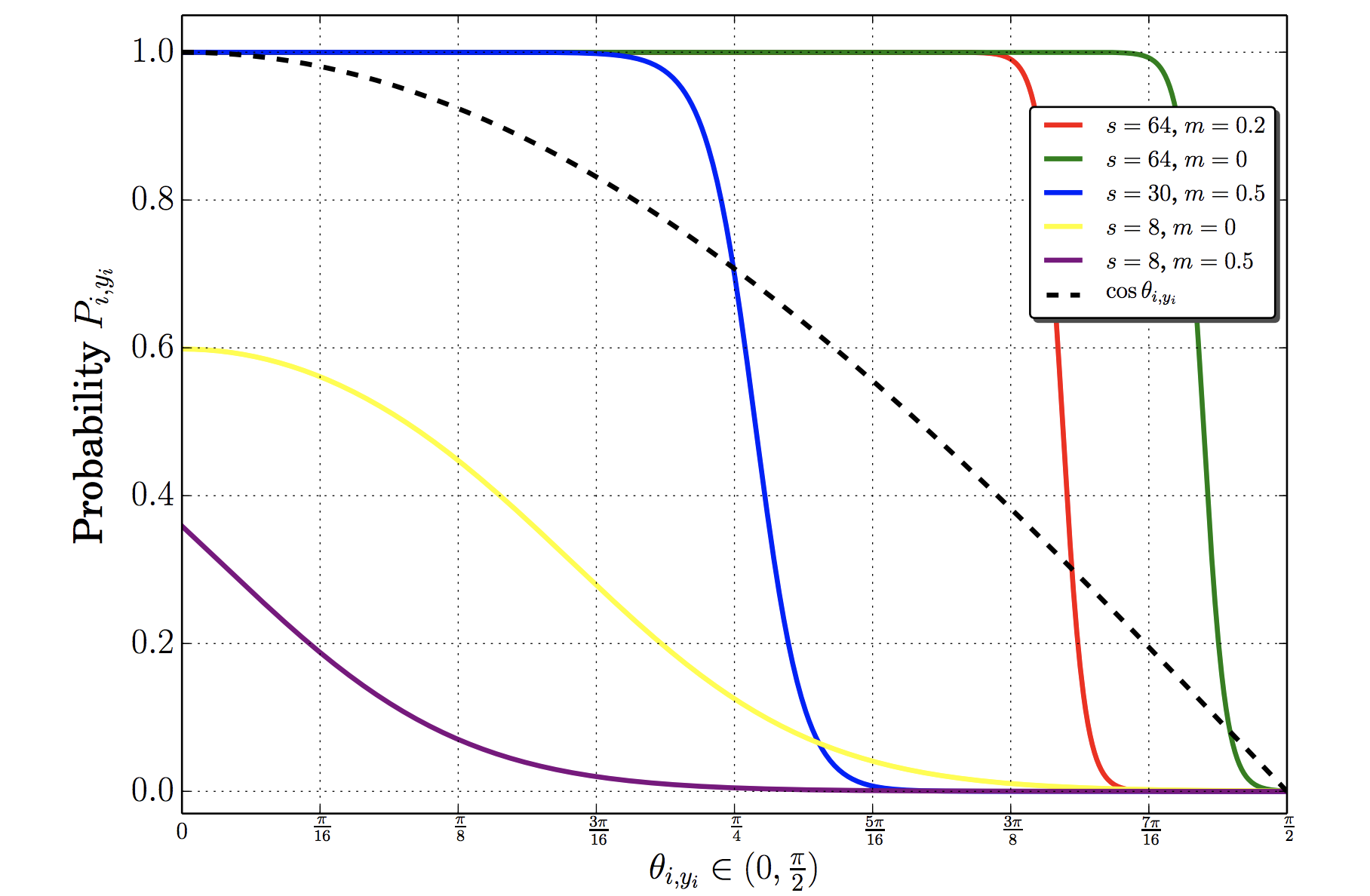
　ここであらためて考えるべきは、ArcFaceの本来の目的です。ArcFaceはクラス分類をしたいのではなく、抽出された２つのベクトル$\vec{x_1}$と$\vec{x_2}$のなす角$\theta$が近いか否かを知りたいのです。つまり、本来的には$\theta_{i,y_i}$の大きさこそが、Backpropagationにおいて重要な勾配の長さ（つまりは、$P_{i,j}$）に影響しなければならないのに、ハイパーパラメータ$s$や$m$が強く関与してしまっています。
　さらに、もうひとつ。$P_{i,y_i}$の値はクラス数$C$によっても変化します。クラス数$C$の増加とともに、不正解のクラス$P_{i,j}$ に割り当てられる確率は、多かれ少なかれ小さくなっていくことが予想されます。これはClosedなクラス分類問題においては合理的です。ただし、これはOpen-Setの問題である顔認識には適していません。

　勾配の長さに影響を与える値として $\nabla f(\cos\theta_{i,j})$ もあります。これはCosine Based Softmax Lossの種類によって異なります。

角度マージンを持たないCosine Based Softmax Lossの場合、

\nabla f(\cos\theta_{i,j}) = s \tag{11}

Cosfaceの場合、

\nabla f(\cos\theta_{i,j}) = s \tag{12}

Arcfaceの場合、

\nabla f(\cos\theta_{i,j}) = s \cdot \frac{\sin(\theta_{i,j} + m)}{\sin\theta_{i,j}} \tag{13}

となります。

つまり、角度マージンを持たないCosine Based Softmax Loss、および Cosfaceにおいては、$\nabla f(\cos\theta_{i,j})$で勾配の長さに与える影響は、常に一定$s$である事を示しています。しかし、Arcfaceでは、勾配の長さと$\theta_{i,j}$は負の相関関係にあり、これは完全に予想に反しています。$\theta_{i,y_i}$が徐々に減少すると、一般的には $P_{i,y_i}$の勾配を短縮する傾向がありますが、Arcfaceでは長さを伸ばす傾向があります。したがって、Arcfaceでは $\nabla f(\cos\theta_{i,j})$が勾配の長さに与える幾何学的な意味は説明されなくなります。

勾配の長さを決定するP2SGradの提案

　ここからがようやく本題で、ハイパーパラメーター、クラス数、logitsのいずれにも依存せず、$\theta_{i,j}$のみによって勾配の長さを決定する新しい方法P2SGradを説明します。P2SGradは特定の損失関数を定義せずに、直接勾配を求めるため、式$(4)$と$(5)$を見直していきます。
　まず、勾配方向はこれまで説明してきた通り、最も最適な方向なのでここを変更する必要はありません。次に、勾配の長さ部分である$P_{i,j}$と$\nabla f(\cos\theta_{i,j})$を考えます。$\nabla f(\cos\theta_{i,j})$に関しては、そもそもハイパーパラメータを除外したいという目的で見直しているので、ここは$1$にしてしまいます。

　次に、$P_{i,j}$ですが $P_{i,j}$の代わりに$\cos\theta_{i,j}$を使う事を考えます。理由は以下の３つです。

• $P_{i,j}$と$\cos\theta_{i,j}$は値の理論範囲$[0, 1]$が同じである。ただし、$\theta_{i,j} \in [0, \pi/2]$とする。
• $P_{i,j}$とは異なり、$\cos\theta_{i,j}$はハイパーパラメーターやクラス数$C$のいずれからも影響を受けることはない。
• 推論時は$\cos\theta$による類似度を元に顔認識を行う。$P_{i,j}$はClosedなクラス分類タスクにのみ適用される確率に過ぎない。

これらを考慮し、新しいP2SGradを定式化します。式$(4)$と$(5)$はそれぞれ式$(14)$と式$(15)$に置き換えられます。

\tilde{G}_{P2SGrad}(\vec{x_i}) = \sum_{j=1}^{C}(\cos\theta_{i,j} - \mathbb{1}(y_i=j)) \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{x_i}} \tag{14}

\tilde{G}_{P2SGrad}(\vec{W_j}) = (\cos\theta_{i,j} - \mathbb{1}(y_i=j)) \cdot \frac{\partial \cos\theta_{i,j}}{\partial \vec{W_j}} \tag{15}

このP2SGradは簡潔ではあるがとても合理的です。$y_i = j$の場合は勾配の長さと$\theta_{i,j}$は正の相関となり、$j \neq y_i$の場合は、負の相関が成り立ちます。

　最後に学習のやり方を説明します。一般的な学習はfoward処理により式$(3)$のCross Entropy Lossを求め、その後、backpropagationにより最終層から式$(4)$と式$(5)$を逆伝播し、各層の重みやバイアスパラメータの勾配を順に求めて行きます。P2SGradを使った学習では、foward処理によって得た特徴量$\vec{x_i}$から直接 式$(14)$と式$(15)$を求めます。後は通常の学習と同じ手順でそれを逆伝播し、各層の重みやバイアスパラメータの勾配を順に求めていきます。

実験

　詳しい実験結果はオリジナル論文を見てもらうとして、参考までにLWFのデータセットで実験した結果を載せておきます。CNN部分はResNet-50を使い、学習のイテレーションと$\theta_{i,y_i}$の平均値の関係を示した図です。

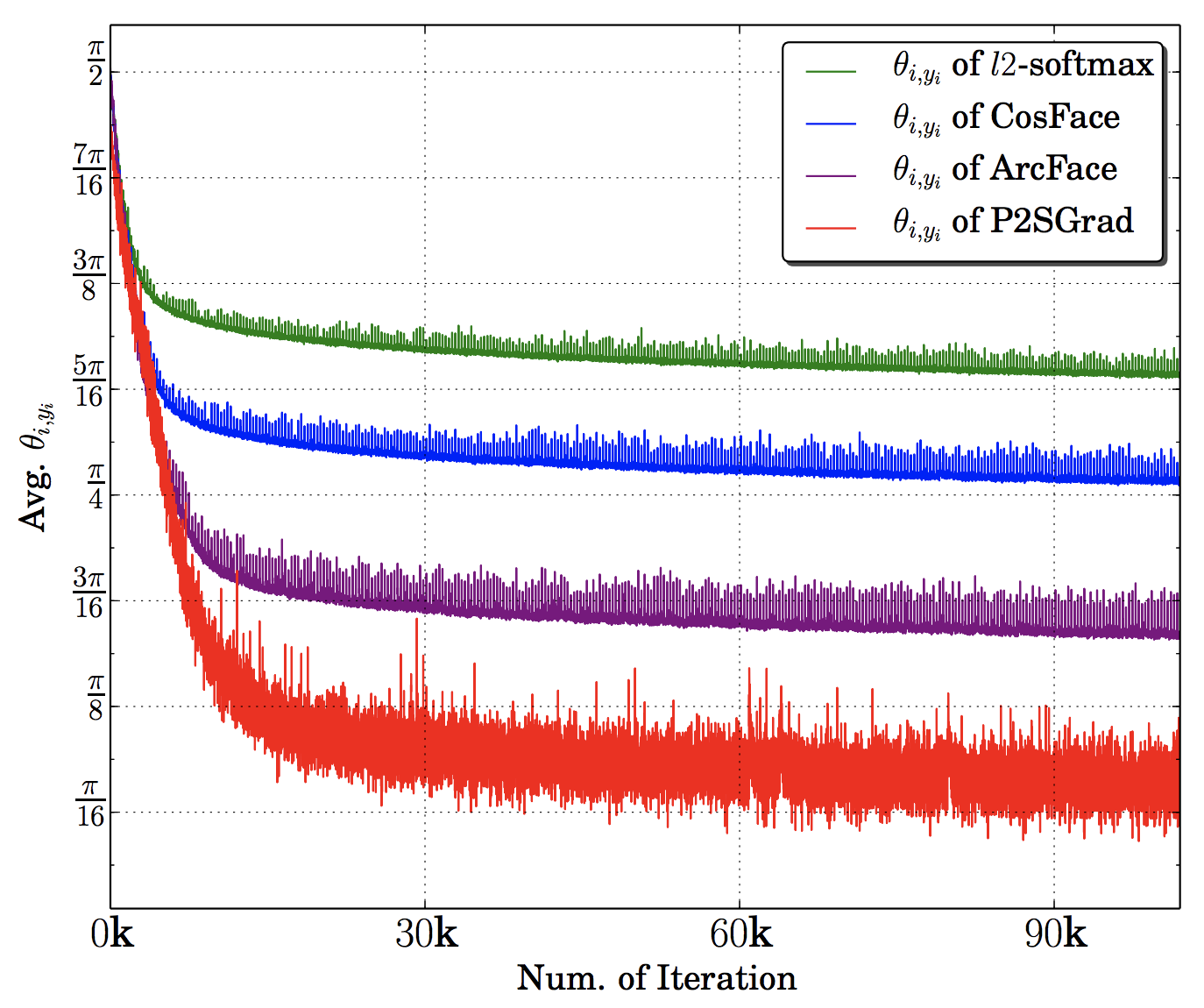
P2SGradによる学習はその他のCosine Based Softmax Lossよりも $\theta_{i,y_i}$の減少が早い事がわかります。

---

1. Y. Wen, K Zhang, Z Li, and Y. Qiao. “A Discriminative Feature Learning Approach for Deep Face Recognition." In ECCV, 2016. ↩

2. W. Liu, Y. Wen, Z. Yu, M. Li, B. Raj, and L. Song. “Sphereface: Deep hypersphere embedding for face recognition.” In CVPR, 2017. ↩

3. H. Wang, Y. Wang, Z. Zhou, X. Ji, D. Gong, J. Zhou, Z. Li, and W. Liu, "CosFace: Large Margin Cosine Loss for Deep Face Recognition," in Proc. of CVPR, 2018. ↩

4. J. Deng, J. Guo, N. Xue, and S. Zafeiriou. "ArcFace: Additive Angular Margin Loss for Deep Face Recognition," In CVPR, 2019. ↩

5. Y. Duan, J. Lu, and J. Zhou. "Uniformface: Learning Deep Equidistributed Representation for Face Recognition." in CVPR, 2019. ↩

6. X. Zhang, R. Zhao, Y. Qiao, X. Wang, and H. Li. "AdaCos: Adaptively Scaling Cosine Logits for Effectively Learning Deep Face Representations." in CVPR, 2019. ↩

7. X. Zhang, R. Zhao, J. Yan, M. Gao, Y. Qiao, X. Wang, and H. Li. "P2SGrad: Refined Gradients for Optimizing Deep Face Models." in CVPR, 2019. ↩