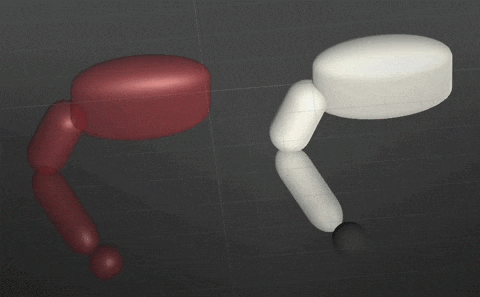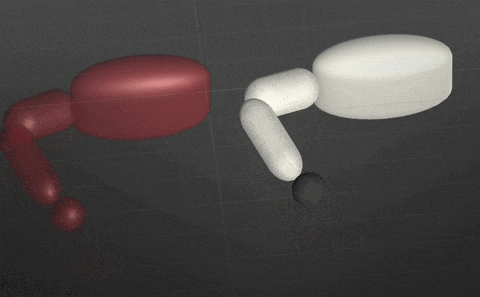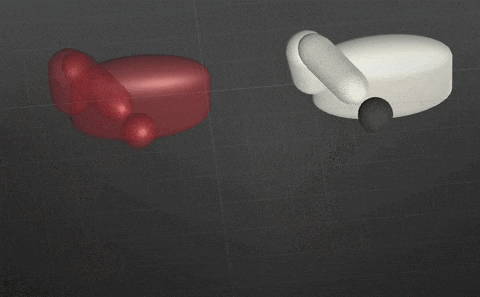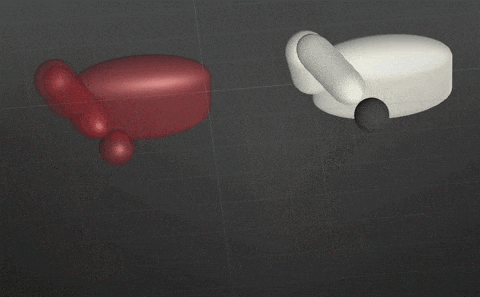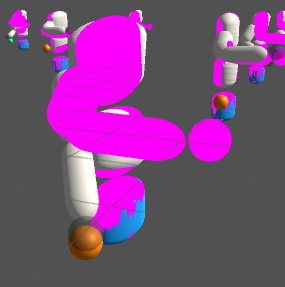LoginSignup
6
4

More than 3 years have passed since last update.

@tanakataiki(tanaka Resercher)

DeepMimicの追実装を試みた YAD2U

Last updated at Posted at 2018-12-13

What this article is for

YAD2U (yet another deepmimic to unity ! )

Other References

Done(Including what can be added instantly)

  • Action Parameters
  • Observation Parameters
  • Random State Distribution
  • Early Termination (If necessary)
  • Made Task Objective Reward (If necessary)
  • PID Control
  • Change Physics integration dt
  • Setting likehood Physical Parameters for each body
  • Record Any Reference State from Rigidbody
  • Applying to other Machine(like arm, walker)
  • MultiAgent Training
  • Reward Construction
  • Return Normalization
  • Change NetWork Architecture
  • Including Visual Observation
  • Add Obeservation Sequence
  • Fixed Record timing
  • Stochastic Momentum Optimizer
  • MultiThreading
  • Skill Selector
  • Transfer Learning for different network size

---Below should be implementd after checking the basic test above---
- [ ] MultiStep Return
- [ ] Multi-Clip Reward
- [ ] Composite Policy
- [ ] Enviromental Retargetting

Variables

変数 範囲 説明
$t$ $0-\infty$ 1ステップ
$s_{t}$ $S_{t} $ 時刻tにおける状態
$a_{t}$ $A_{t}$ 時刻tにおける行動
$r_{t}$ $R_{t} $ 時刻tにおける報酬
$\pi_{(s_{t},a_{t})}$ $\pi:S\times A$$\pi \in [0,1]$ エージェントが環境に対してとる行動を状態に基づき決定するための確率分布
$R_{(s_{t},a_{t})}$ $R$ 状態sの時に行動aをとった時に環境がエージェントに与える報酬
$V_{(s_{t})}$ $V_{s_{t}}:S\rightarrow R$ 状態sから開始して方策$\pi$に従ってエージェントが行動した場合に得られる収益の期待値
$A_{t}$ $A_{t}=R_{(s_{t},a_{t})}-V_{(s_{t})}$ 推定収益
$\gamma$ $\gamma \in [0,1]$ 1~nステップ後の報酬の割引率
$\lambda$ $\lambda \in [0,1]$ 1~nステップ後の推定利益の割引率
$\tau_{(s_{t+1}:s_{t},a_{t})}$ $\tau:S\times\ A \times S$$\tau\in [0,1]$ 環境が状態sの時にエージェントがaという行動をとった時に次の状態$s^{'}$に遷移する確率

Intro

（シミュレーション側）
・人や動物のモデルを用いた現実に限りなく近い物理ベースシミュレーションの作成は重要な課題である．
（制御側）
・強化学習によってさまざまなスキルを獲得している例はあるが，モーションがきれいではない．
・モーションキャプチャーデータを用いた運動学的制御手法によるスキル習得はできるが，
新たなタスクに対応できるほど汎用性は高くない．
一方で，強化学習を用いた試行錯誤手法をモーションキャプチャーデータと合わせることによって
スキルの習得とタスクの実現を同時に行うことを可能にするという提案手法がDeepMimicである．(ざっくりと)

Summary

キャラクターモデル，Referenceのキャラクターの運動学モデルと，報酬関数により定義されたタスクを入力とする．
キャラクターはReferenceMotionの模倣をしながら，タスクを遂行する．
制御の方策関数(Policy)$\pi(a_{t}|s_{t},g_{t})$はキャラクタの状態$s_{t}$とタスク$g_{t}$によって行動$a_{t}$を決める．
それぞれの行動$a_{t}$はキャラクタのジョイントのtargetAngleを決定し，
PDコントローラによりそれぞれのジョイントの入力トルクを決める．
また，
・ReferenceMotionはImitationReward $r^{I}(s_{t},a_{t})$の設計に使用される．
・タスクの設定はTaskSpecificReward$r^{G}(s_{t},a_{t},g_{t})$の設計及に使用される．

MultiAgent&MultiThreading

マルチエージェントAgentが経験を積み重ねていく，さらに全スレッドで共有しているParameterServerがある．
マルチエージェントによる分散学習勾配更新のタイミングは一定ステップ経つかTerminationが起こった時で，各スレッドが非同期に勝手なタイミングで更新する．
多いほうがLocalMinimumに陥りにくく安定する．

配色ミスにより通常の16倍きもかったｗｗ
MultiThread.gif

multiThreading.PNG

DeepMimicについて

A longstanding goal in character animation is to combine data-driven specification of behavior with a system that can execute a similar behavior in a physical simulation.
reference.png

State and Action

State

キャラクタの状態はRootからの相対的な以下の値を観測値として扱う．
・各リンクの位置
・各リンクの回転角のクオータニオン表現
・各リンクの並進速度
・各リンクの回転角速度
・周期運動の位相$\phi$
全ての特徴はキャラクタのローカル座標をもとに計算しており，Rootを原点としている．また，Rootが向いている方向をx軸とした．（追実装ではｚ軸とした）

Action

方策からの行動は３０Hz周期で与えられ，各関節に取り付けられたPDコントローラに目標回転角を与えることで実現している．

Network Architecture

HeightmapはHLCで32×32
8×8畳み込み16
4×4畳み込み32
4×4畳み込み32
全結合層64
＋
全結合層1024
全結合層512
で作る
deep_mimic_network.png

「Early Termination」

シミュレーションは有限時間で行うことになるが，それぞれのシミュレーションにおいて，ある待った時間間隔，またはある特定の終了条件を満たしたとき
胸が地面についたとき，などを境に学習を終了することでより良い値が得られる．

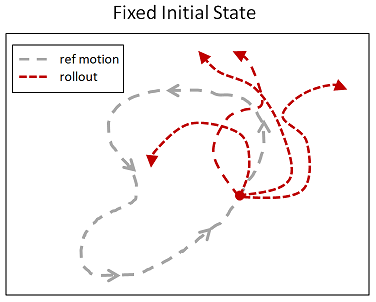
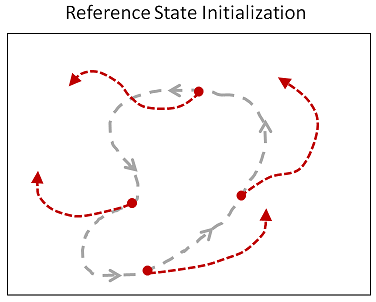
「Reference State Initialization (RSI)」

キャラクタの初期姿勢をランダムに決定することは局所解に陥ってしまうことを防ぐことができ，有効な手法であるが，バク転のようにタスクが難しく，成功の可否が初期姿勢に依存してしまうものは学習しても成功する確率は低く，有効ではない．そこで，キャラクタ（Agent）にヒントを与える為にReferenceMotionの姿勢からランダムに初期姿勢を取り出し，キャラクタの初期姿勢として学習を進めることで，どの状態がより大きな報酬を得ることができるのかを局所解に陥る前に学習することができる．

FSI.pngRSI.png
MimicRSD.gif

Reward

Immitation Objective

報酬はクオータニオンの差分，角速度の差分，エンドエフェクタの位置の差分，重心の位置の差分によって算出される．
Reward $r^{t}$ at each step t consists of two terms that encourage the charactor to match the reference motion while also saisfiyng additional task objective.
・quatenion difference
$$r^{p}_{t}=exp[-2(\Sigma _{j} ||\hat{q}^{j} _{t}\ominus q^{j} _{t}||)]$$

・joints velocity difference
$$r^{v}_{t}=exp[-0.1(\Sigma _{j} ||\hat{\dot{q}}^{j} _{t}- \dot{q}^{j} _{t}||^{2})]$$

・endeffector position difference
$$r^{e}_{t}=exp[-40(\Sigma _{e} ||\hat{q}^{e} _{t}- q^{e} _{t}||^{2})]$$

・center of mass reward
$$r^{c}_{t}=exp[-10(\Sigma _{j} ||\hat{q}^{c} _{t}- q^{c} _{t}||^{2})]$$

Task Objetive

[x] Target Heading

Agentを目標は指定した方向に誘導すること．
ターゲットの二次元平面での方向を$d_{t}$，目標速度$v$,Agentの重心速度を$v_{t}$とし，報酬$r_{t}^{G}$は以下のように与えられる．
speedのオーバーに関してはペナルティを与えないスタイル．
論文には書いてないが，CoMは相対位置なのに対して，CoM'は絶対速度であると思われる．
$$r_{t}^{G}=exp[-2.5max(0,v-v_{t}^{T}d_{t})^{2}]$$

[x] Strike

Agentの目標はランダムに配置されたゴールをAgentのEndEffectorでヒットすること．
報酬はターゲットの位置$p_{t}^{tar}$とEndEffectorリンクの位置$p_{t}^{e}$を用いて以下のようにあらわされる．
$$r_{t}^{G}= \begin{cases}
1 & (target has been hit) \\
exp[-4||p_{t}^{tar}-p_{t}^{e}||^{2} & (otherwise)
\end{cases}$$

MultiSkill Integration

1.一つのReferenceMotionに縛られないより柔軟なMulti-Clip　Reward
2.Skill Selector Policyを利用することでどのスキルを使用するのかOneHot形式で入力
3.毎クリップごとに新しいPolicyを学習することを避ける為に，Single-clip Policyではなく，
Composite Policyというものを用いて，それぞれのPolicyを個別に学習し，
実行時にどのPolicyを使用するかを決定する．

Multi-Clip Reward

j個のMtionClipの中からImitation Objectiveの報酬が最大となるようにMtionClipの選択をする．
$$ r_{j}^{I_{t}}= MAX _{j=1..k}$$
ここでの $r^{j} _{t}$ はj番目のクリップフレームに関するImitation Objetiveである．
この際，似ている動作が学習しやすく，CompositePolicyが効率の良い学習を可能にする．

Skill Selector

Onehotのベクトル表現によるスキルの選択
最初と最後のフレームは同じ周期で動かさなければならないため，複製して周期を合わせる．
本実装ではSelectorPolicyは利用していない．

Composite Policy

Toward SPDController

Conventional PD Controller

$q$を現在の位置，$\dot{q}$を現在の速度とし，$\bar{q}$を目標の位置，$k_{p}$，$k_{d}$に関してはお察しの通り．
とするとPDコントローラーは以下のように書ける．
$$\tau^{n}=-k_{p}(q^{n}-\bar{q}^{n})-k_{d}\dot{q}^{n}$$
しかしながら，このような古典的な方法だと，目標位置と現在位置の差分が大きい場合には，ゲインを大きくしなければならない．
そうすると，コントローラの安定性が低くなってしまい，効率と，安定性のトレードオフになってしまう．

Stable　PDController

そこで現在の状態$q^{n}$を用いずに次のタイムステップである$q^{n+1}$を計算に用いることにする．
次のステップを用いるとPDコントローラーは以下のように書ける．
$$\tau^{n}=-k_{p}(q^{n+1}-\bar{q}^{n+1})-k_{d}\dot{q}^{n+1}$$
しかしながら，我々は次のタイムステップについて知らないので，テイラー展開を用いて1次近似を行う．
$$q^{n+1}=q^{n}+\delta t\dot{q}$$ $$\dot{q}^{n+1}=\dot{q}^{n}+\delta t\ddot{q}$$
上記の式により SDPコントローラは以下のように書ける
$$\tau^{n}=-k_{p}(q^{n}+\delta t\dot{q}^{n}-\bar{q}^{n+1})-k_{d}(\dot{q}^{n}+\delta t \ddot{q})$$
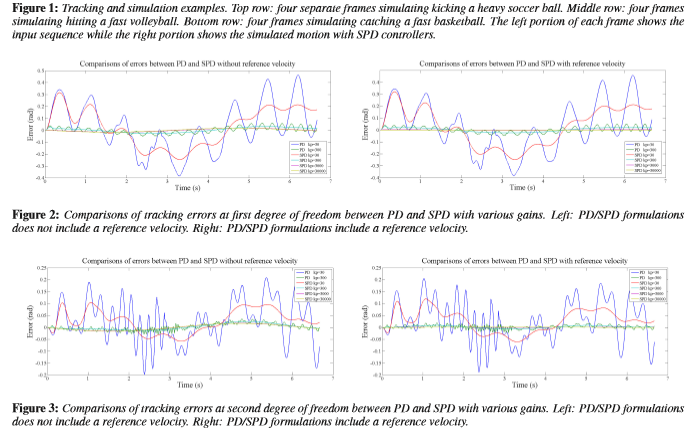
また，古典的なPDサーボではトラッキングの遅延を減らすために，ReferenceVelocityが使われることがある．このReferenceVelocityは解析的に，または数値的に計算することができる．
$$\tau^{n}=-k_{p}(q^{n}-\bar{q}^{n})-k_{d}(\dot{q}^{n}-\bar{\dot{q}}^{n})$$
SPDもまた，ReferenceVelocityをトラッキングの遅延を減らすために使用することとした．
ゆえに式は以下のようになる．
$$\tau^{n}=-k_{p}(q^{n}+\delta t\dot{q}^{n}-\bar{q}^{n+1})-k_{d}(\dot{q}^{n}+\delta t \ddot{q}-\bar{\dot{q}}^{n+1})$$
まとめると，
遅延考慮なし$\tau^{n}=-k_{p}(q^{n}+\delta t\dot{q}^{n}-\bar{q}^{n+1})-k_{d}(\dot{q}^{n}+\delta t \ddot{q})$
遅延考慮あり$\tau^{n}=-k_{p}(q^{n}+\delta t\dot{q}^{n}-\bar{q}^{n+1})-k_{d}(\dot{q}^{n}+\delta t \ddot{q}-\bar{\dot{q}}^{n+1})$
SPDの論文によると，ReferenceVelocity無しで制御しているそしてDeepMimicはReferenceVelocity無し．
制御にReferenceを前提として話してしまったあたり相当Deepmimicに侵されている気がする．
stablePDwithref.PNG

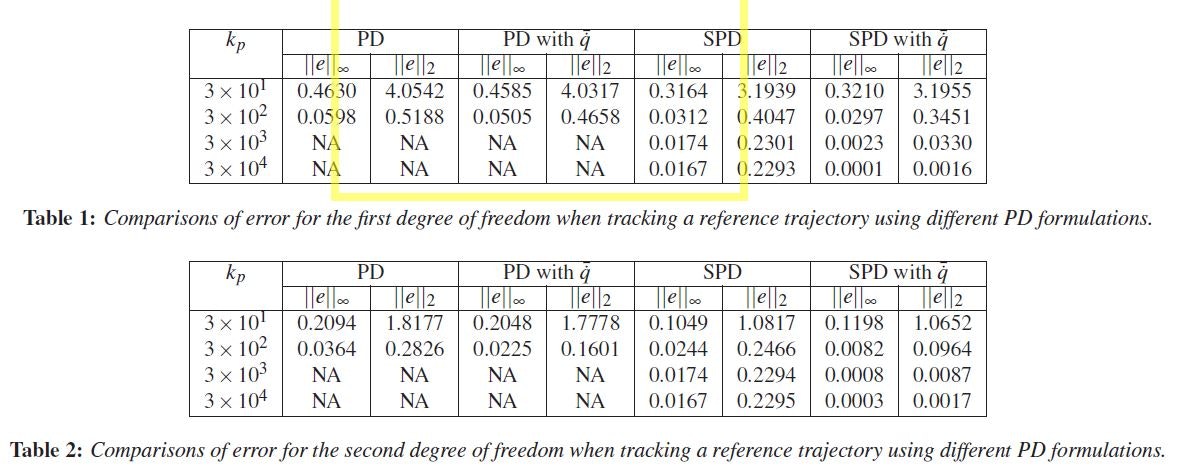
Some Tips for SPDController

Ensure Stability

$k_{d}>k_{p}\delta t$が安定性を保証してくれる．
今回のDeepMimicでのパラメータ$k_{p}$，$k_{d}$とすべての関節において一定の値．

Parameters for two link pendulum

spdParameters.JPG

Parameters for simulation

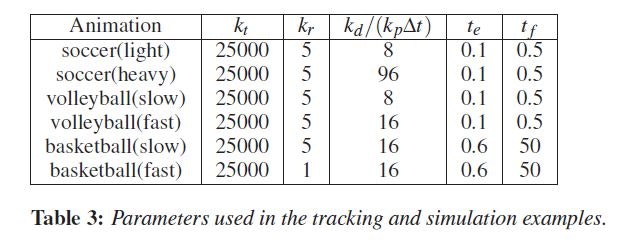
spdParameter4Simulation.JPG
と作ってみたが，角加速度は数値微分で求めたし，６０Hzで制御回すことないからタイムステップnだけ用いた．ｗｗ

PPO Flow Chart

1: $\hspace{0mm}$Policy $\theta \leftarrow$ random weight
2: $\hspace{0mm}$Value Function$\psi\leftarrow$ random weights
3: $\hspace{0mm}$while ETまで
4: $\hspace{8mm}$$s_{0}$にReferenceMotionの初期状態を代入
5: $\hspace{8mm}$Agentの状態を$s_{0}$で初期化
6: $\hspace{8mm}$for step1~mまで
7: $\hspace{16mm}$$s$$\leftarrow$初期状態
8: $\hspace{16mm}$$a$~$\pi_{\theta}(a|s)$
9: $\hspace{16mm}$1ステップ進める
10:$\hspace{16mm}$$s^{'} \leftarrow$end state
11:$\hspace{16mm}$$r \leftarrow$ reward
12:$\hspace{16mm}$(s,a,r,$s{'}$)をmemoryに記録
13:$\hspace{8mm}$end for
14:$\hspace{8mm}$$\theta_{old}\leftarrow\theta$
15:$\hspace{8mm}$それぞれの更新ステップで
16:$\hspace{8mm}$$n$個のサンプルミニバッチ$(s_{i},a_{i},r_{i},s_{i}')$をmemoryのDから取り出す．
17:$\hspace{8mm}$Value関数の更新
18:$\hspace{8mm}$for each $(s_{i},a_{i},r_{i},s_{i}')$ do
19:$\hspace{16mm}$$y_{i}\leftarrow$ compute target value using TD($\lambda$)
20:$\hspace{8mm}$forループ終了
21:$\hspace{8mm}$$\psi \leftarrow \psi +\alpha_{v}(\frac{1}{n} \Sigma_{i} \nabla_{\psi}V_{\psi}(s_{i})-V(s_{i}))$
22:$\hspace{8mm}$Policyのアップデート
23:$\hspace{8mm}$for each $(s_{i},a_{i},r_{i},s_{i}')$ do
24:$\hspace{24mm}$$A_{i}\leftarrow$ compute advantage using $V_{\psi}$ and GAE
25:$\hspace{24mm}$$w_{i}(\theta)\leftarrow \frac{\pi_{\theta}(a_{i}|s_{i})}{\pi_{\theta_{old}}(a_{i}|s_{i})}$
26:$\hspace{16mm}$forループ終了
27:$\hspace{16mm}$$\theta\leftarrow \theta+a_{\pi}\frac{1}{n}\Sigma_{i}\nabla_{\theta}min(w_{i}(\theta)A_{i},clip(w_{i}(\theta),1-\epsilon,1+\epsilon)A_{i})$報酬のクリッピング
29:$\hspace{8mm}$forループ終了
30:$\hspace{0mm}$1ループ終了

Body Parts Info

身長170㎝，体重70㎏の人の体の重さは一般的な平均体系をもとに頭部7％、胴体43％、上腕3.5％、前腕2.5％、掌・手指0.8％大腿11％、下腿5.4％、足1.8％と換算すると以下のようになる．
頭部11.9kg
胴体7.31kg
上腕5.95％
前腕4.25kg
手指1.36kg
大腿18.7kg
下腿9.18kg
足 3.06kg

Interpolation4Quaternion

オイラー角はジンバルロックや姿勢角が一意に求まらない可能性があり，四元数を用いている．
筆者の環境上角速度を直接取ってこれなかったため，四元数差分→オイラー角とし，線形補間を用いて角速度とした．
実際の関数としてはないが，概念として以下に示す．．．程のことでもないか．．．単純に角度差分とするよりも，滑らかな値になる．
$$Velocity=\frac{Quaternion*Quaternion_{pre}^{-1}}{dt}$$
$$SlerpVelocity=Interpolate(a*Velocity+(1-a)*Velocity_{pre})$$
と作ってみたが，物理エンジンは480Hzで回したし，多少の誤差はPPOが埋めてくれるでしょう．ということで最終的にa=1とした．ｗｗ
ひとこと一応試してみた結果いい感じの結論が出たと言いたい．．．

HeightMap

高さｚ方向の値のみを格納したMap
Environmental　Retargetting時に使用する
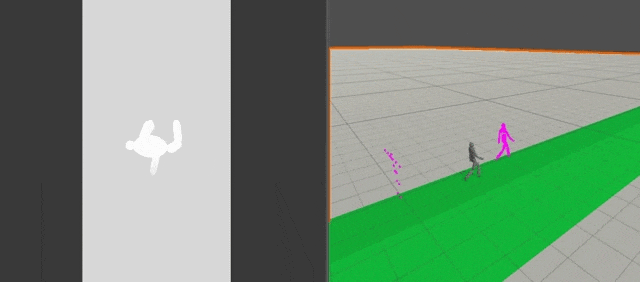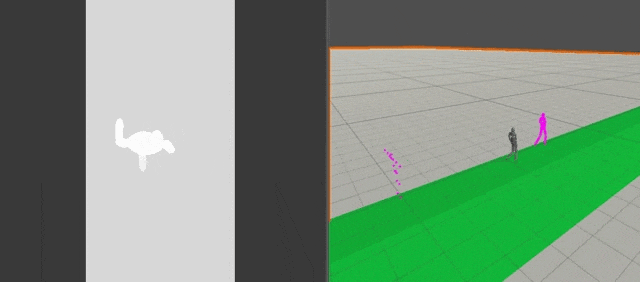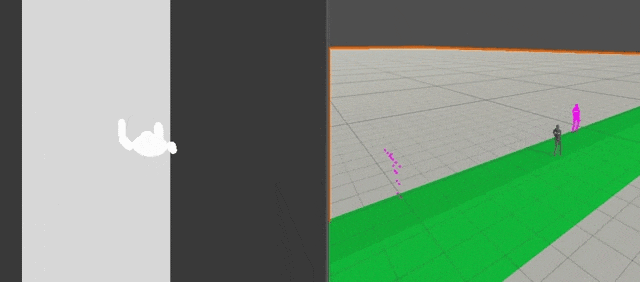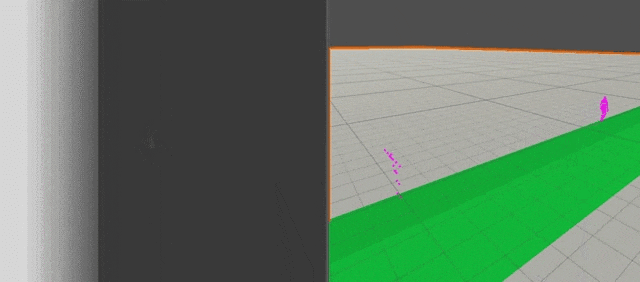
heightmap.gif

32×32の１０m四方の領域をサンプリングしている．
フレームレートは４FPSにしてデフォルトの３０FPSからちょっと落としている．

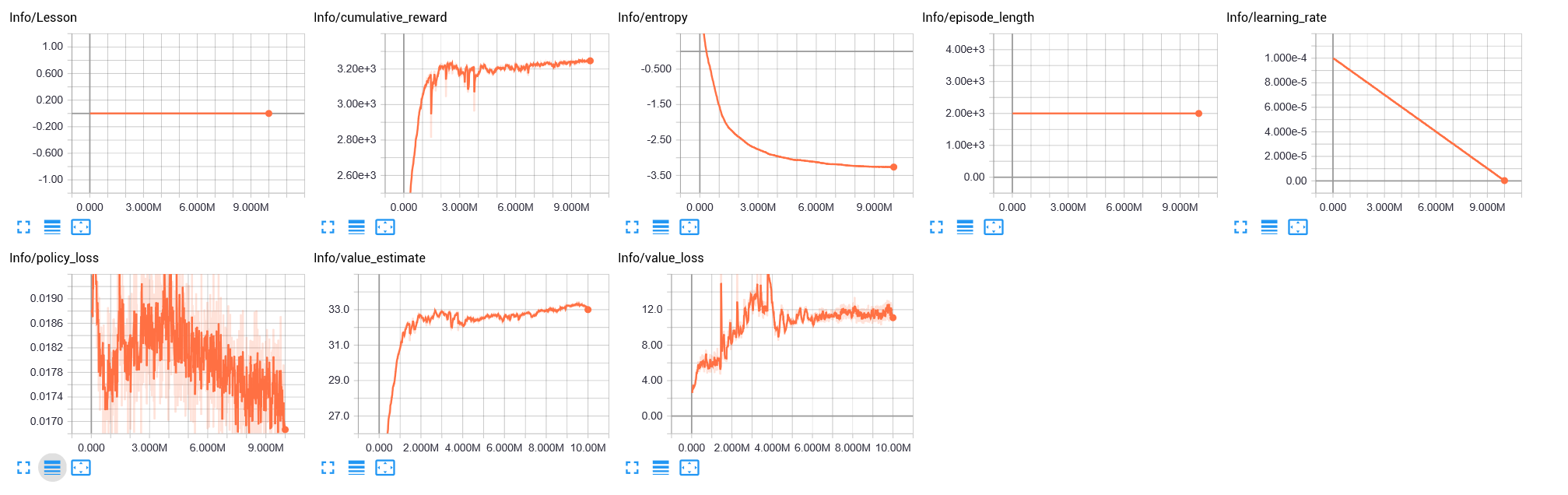
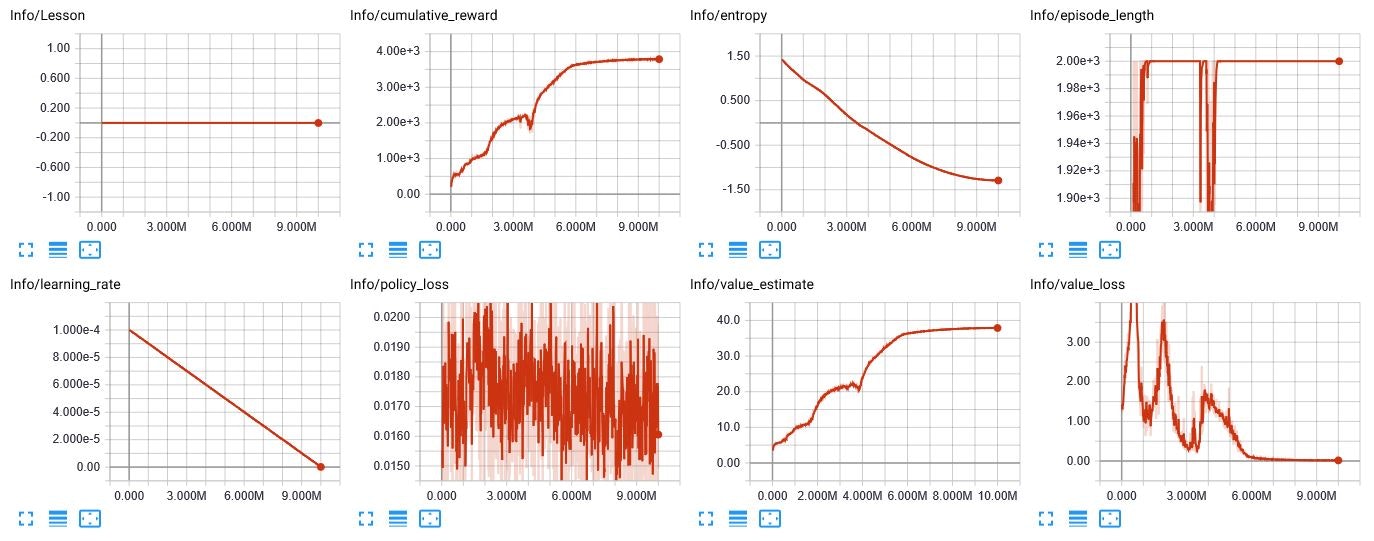
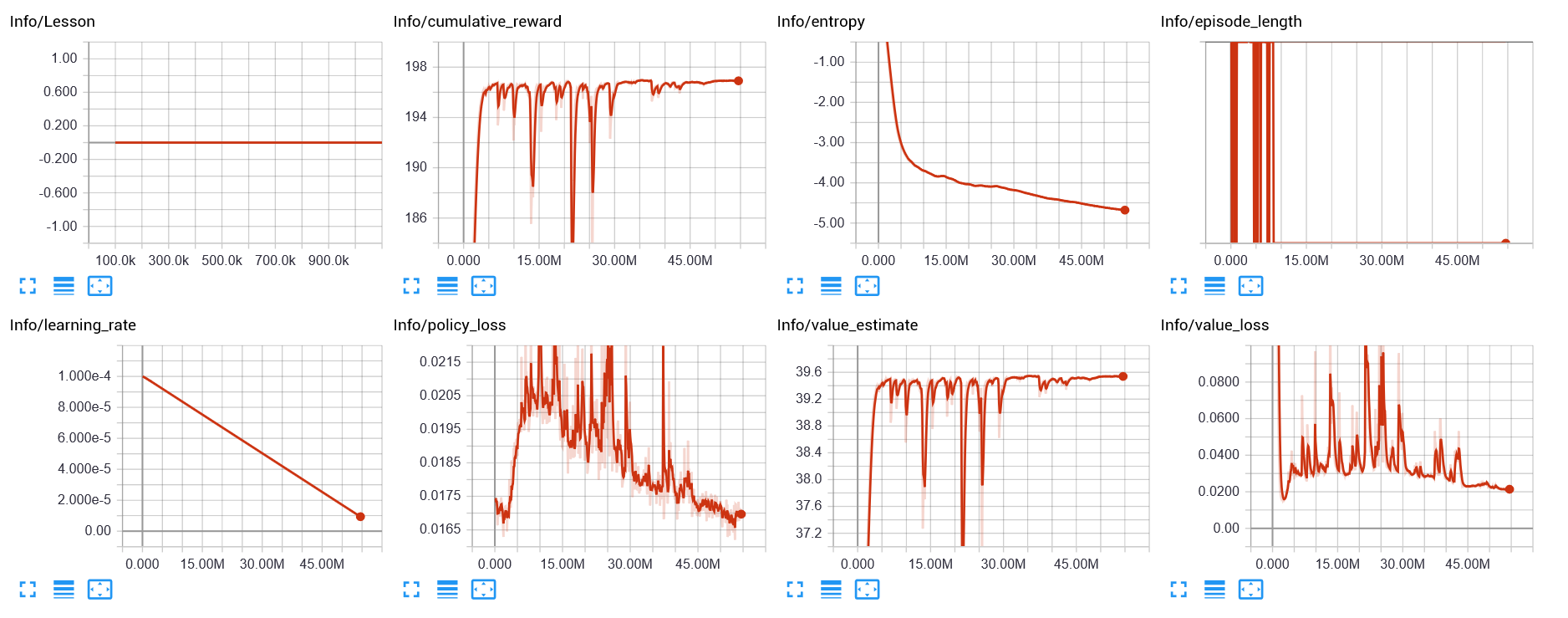
結果

Immitation Objective

学習による改善の余地はもう少しありそう
2018/9/25
armTensorboard.PNG

simpleArmerresult.gif

2018/10/6
tensormimicarm.JPG

armerMimic.gif

Task Objective

SimpleArm

2018/10/10
armerTaskObj.PNG

armTaskObj.gif

白のAgentは赤のReferenceからほんの少し外れて球を触りいっている．

MultiArm

2018/10/25
ArmMimic.gif
配色同じでキモイｗｗ（まだ学習中）

SkillSelector

SkillSelectorV4.gif
それぞれ独自に学習した結果を合わせ，複数のスキルを実行できる．
左右も加えたければ加えられる，ま，ちょっと時間かかるからまた今度．．．
これはUIを頑張った！

Task＆Immitation

overtask.PNG

Arm480HzTAsk0.5.gif
TaskObjective0.5
ImmitationObjective0.5
Taskの重みが大きすぎてImmitaitonを無視してTaskCompleteしてからImmitationを始める始末

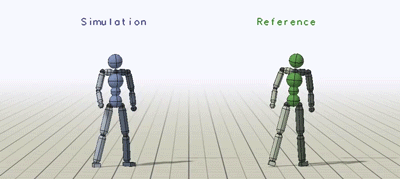
Example-Guided DeepRL

赤がReferenceグレーがAgent

Running(In the middle of training)

2018/12/4
Running04.gif

2018/12/6
Running2.gif

2018/12/11
Walk.gif
Walkingのほうが学習しやすかったみたいま，角速度小さいし当たり前か

Walktest2.gif

Finally

Agent Immitates to walk

walk.gif

MultiTaskArm+

2019/03/18
You can choose below 7 Different Mode with your gui
・4 Independently Trained Task
・WaitMode
・Manual Mode with keyboard input
・dangerous Mode lol

This white reinforcement learned agent satisfy
・Immitation Objective　(yellow text
・With additional strike objective (red text
The yellow agent is reference
SE4.gif

What makes this difficult

3次元での現実に即したシミュレーションの作成となると，トルク，拘束力，Gimbal Lock，重力，時間，質量，モーメント，四元数，ステップ数，シミュレータ周期など様々な要因が絡まってくるため因果関係がものすごく複雑になるところ．

感想

Jasonさん(著者)ありがとう．よくまあこんな複雑なシステムを作ったなあと思う

終わりに

この実装はSE4（元Fove）の開発のバイトとして行ったものです．
SE4のみなさんありがとうございました．
バイト生も募集しているそうです．（要スキル）
http://se4.space/

企業のかた

研究者の方

アドバイスなど待ってます！

Reference

DeepMimic
https://bair.berkeley.edu/blog/2018/04/10/virtual-stuntman/
https://arxiv.org/abs/1804.02717
http://blog.syundo.org/post/20180503-deep-mimic/
A3C
https://arxiv.org/pdf/1602.01783.pdf
https://qiita.com/sugulu/items/8925d170f030878d6582
PPO
https://arxiv.org/abs/1707.06347
https://qiita.com/keisuke-nakata/items/87b742bcb09149b6d8d1

MachineSpec

CPU : Dual CPU Xenon v3 8core×2 RAM 128 GB
GPU : 1080Ti

Code

Sample

6
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
4