最近強化学習にハマってます。強化学習やってると, やっぱり棒を立てたくなってしまうのが男ってもんですよね。というわけで, 前回に引き続きOpenAIGymのCartPoleをやってみたので紹介します。
前回の記事 強化学習で山を登りたい
SARSA学習法とは
前回の記事で触れたQ学習ですが, 今回はSARSAという手法を用いたいと思います。ではおさらいです。強化学習における状態行動価値Qの更新は,
$$\begin{aligned}Q\left( s_{t},a_{t}\right) \ \leftarrow Q\left( s_{t},a_{t}\right) \ +\alpha \left( G_{t}-Q\left( s_{t},a_{t}\right) \right) \end{aligned}$$
を一回の状態遷移ごとに行います。SARSAとQ学習の違いは, この$G_{t}$の決め方です。
Q学習の場合
$$G_{t}=r_{t+1}+\gamma\max_{a\in At}[Q(s_{t+1},a)]$$
SARSAの場合
$$G_{t}=r_{t+1}+\gamma Q(s_{t+1},a_{t+1}^{\pi})$$
ここで, $a_{t+1}^{\pi}$とは, 状態$s_{t+1}$において方策に従って次の行動を選んだときの行動を示しています。以上からわかることは, Q学習では値の更新にmaxを使っている, つまり得られるであろう最大の状態価値を用いて更新を行っているいはば楽観的な学習方法であることに対し, SARSAでは, 次の行動を考慮に入れているため, より現実的な方策の決定方法になっています。今回は, これらの比較も行っていきます。
CartPoleルール

この棒を長い間(200step)立て続ければクリアという形式です。与えられる状態は四つで, 台車の位置, 台車の速度, ポールの角度, ポールの角速度が与えられます。行動は, 左に台車を押す:0, 右に押す:1の2つに制限されます。ポールの角度が12度以上傾くか, 200ステップ耐久で終了です。
実装
まずはライブラリをインポートします。
import gym
from gym import logger as gymlogger
gymlogger.set_level(40) #error only
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import math
import glob
import io
import base64
学習を実装するクラスSARSAを定義します。
class SARSA:
def __init__(self, env):
self.env = env
self.env_low = self.env.observation_space.low # 状態最小値
self.env_high = self.env.observation_space.high # 状態最大値
tmp = [7,7,7,7] #状態を7つの状態に分ける
self.env_dx = [0,0,0,0]
self.env_dx[0] = (self.env_high[0] - self.env_low[0]) / tmp[0]
self.env_dx[1] = (self.env_high[1] - self.env_low[1]) / tmp[1]
self.env_dx[2] = (self.env_high[2] - self.env_low[2]) / tmp[2]
self.env_dx[3] = (self.env_high[3] - self.env_low[3]) / tmp[3]
self.q_table = np.zeros((tmp[0],tmp[1],tmp[2],tmp[3],2)) #状態価値関数の初期化
def get_status(self, _observation): #状態を離散化する
s1 = int((_observation[0] - self.env_low[0])/self.env_dx[0]) #7つの状態のいづれかに落とし込む
if _observation[1] < -1.5: #自分で分類する
s2 = 0
elif -1.5 <= _observation[1] < - 1:
s2 = 1
elif -1 <= _observation[1] < -0.5:
s2 = 2
elif -0.5 <= _observation[1] < 0.5:
s2 = 3
elif 0.5 <= _observation[1] < 1.5:
s2 = 4
elif 1.5 <= _observation[1] < 2:
s2 = 5
elif 2 <= _observation[1]:
s2 = 6
s3 = int((_observation[2] - self.env_low[2])/self.env_dx[2]) #7つの状態のいづれかに落とし込む
if _observation[3] < -1: #自分で分類する
s4 = 0
elif -1 <= _observation[3] < -0.7:
s4 = 1
elif -0.7 <= _observation[3] < -0.6:
s4 = 2
elif -0.6 <= _observation[3] < -0.5:
s4 = 3
elif -0.5 <= _observation[3] < -0.4:
s4 = 4
elif -0.4 <= _observation[3] < -0.4:
s4 = 5
else:
s4 = 6
return s1, s2, s3, s4
def policy(self, s, epi): #状態sにおける行動を選択する
epsilon = 0.5 * (1 / (epi + 1))
if np.random.random() <= epsilon:
return np.random.randint(2) #ランダムに選ぶ
else:
s1, s2, s3, s4 = self.get_status(s)
return np.argmax(self.q_table[s1][s2][s3][s4]) #行動価値が最大の行動を選択する
def learn(self, time = 200, alpha = 0.5, gamma = 0.99): #time回数だけ学習を行う
log = [] #1エピソードごとの合計報酬を記録
t_log = [] #1エピソードごとのステップ数を記録
for j in range(time+1):
t = 0 #ステップ数
total = 0 #合計報酬
s = self.env.reset()
done = False
while not done:
t += 1
a = self.policy(s, j)
next_s, reward, done, _ = self.env.step(a)
reward = t/10 #長い間耐久すればするほど報酬は増える
if done:
if t < 195:
reward -= 1000 #耐久に失敗したら罰則
else:
reward = 1000 #成功時はもっと報酬を与える
total += reward
s1, s2, s3, s4 = self.get_status(next_s)
G = reward + gamma * self.q_table[s1][s2][s3][s4][self.policy(next_s, j)] #累積報酬の計算
s1, s2, s3, s4 = self.get_status(s)
self.q_table[s1][s2][s3][s4][a] += alpha*(G - self.q_table[s1][s2][s3][s4][a]) #Qの更新
s = next_s
t_log.append(t)
log.append(total)
if j %1000 == 0:
print(str(j) + " ===total reward=== : " + str(total))
return plt.plot(t_log)
def show(self): #学習結果を表示
s = self.env.reset()
img = self.env.render()
done = False
t = 0
while not done:
t += 1
a = self.policy(s, 10000)
s, _, done, _ = self.env.step(a)
self.env.render()
print(t)
self.env.reset()
self.env.close()
困ったポイント
ここで自分がつまずいたところを紹介します。__init__のところで, env_dxで四つの状態それぞれについて, 離散化するための前準備をしているのですが, ここである問題が生じました. レファレンスをよく見ると,

速度の値の可変領域がinfです。そう, 無限なんです!
これでは, env_dxの値も無限になってしまって, 連続値の離散化がうまくいきません。そこで,
from random import random
env.step(random.randint(2))
を何度も実行して, 台車の速度, それからポールの角速度の変異を観察しました。すると,
if _observation[1] < -1.5: #台車の速度
s2 = 0
elif -1.5 <= _observation[1] < - 1:
s2 = 1
elif -1 <= _observation[1] < -0.5:
s2 = 2
elif -0.5 <= _observation[1] < 0.5:
s2 = 3
elif 0.5 <= _observation[1] < 1.5:
s2 = 4
elif 1.5 <= _observation[1] < 2:
s2 = 5
elif 2 <= _observation[1]:
s2 = 6
if _observation[3] < -1: #ポールの角速度
s4 = 0
elif -1 <= _observation[3] < -0.7:
s4 = 1
elif -0.7 <= _observation[3] < -0.6:
s4 = 2
elif -0.6 <= _observation[3] < -0.5:
s4 = 3
elif -0.5 <= _observation[3] < -0.4:
s4 = 4
elif -0.4 <= _observation[3] < -0.4:
s4 = 5
else:
s4 = 6
こんな感じで分類できそうということに気づきました。
学習
そんなこんなで学習。3000回くらいで余裕っしょってことで。
env = gym.make('CartPole-v0')
agent = SARSA(env)
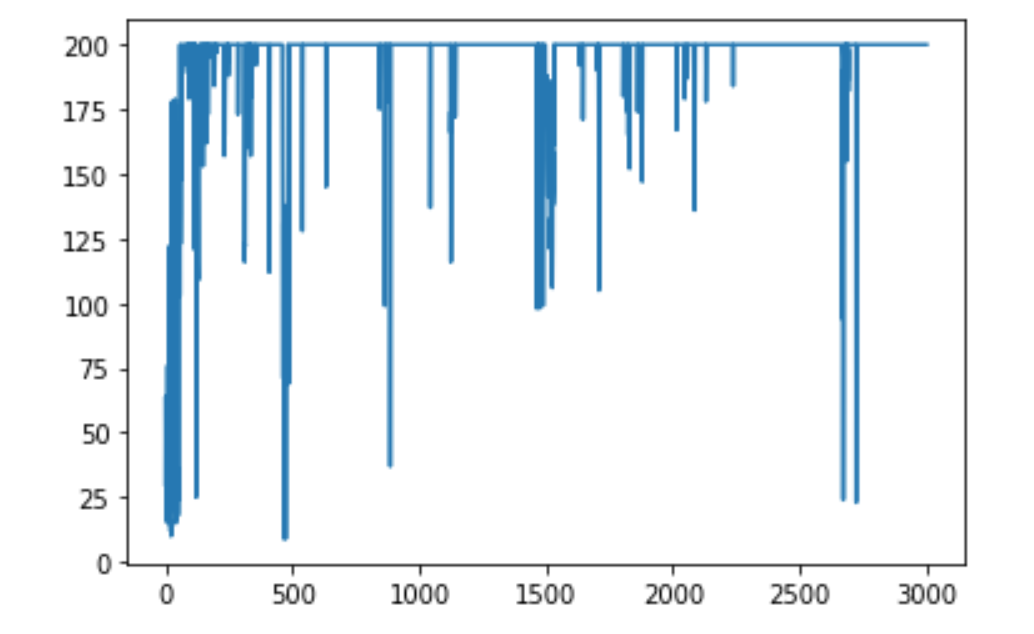
agent.learn(time = 3000)
さて, agent.show()でアニメーションで確認してみましょう。

かなり安定していて持続力がすごいですね。これでめでたく男になれました。
Q学習vsSARSA
この環境においてQ学習とSARSAを比較してみます。Q学習ではGを
G = reward + gamma * max(self.q_table[s1][s2][s3][s4])
のようにします。これで学習してみると,

収束の安定性が, SARSAの方が一枚上手に見えます。男ならSARSAのように現実をみろってことですね。はい。
感想
この環境だと, 状態の離散化が一番大変なところなのかなと思いました。そこを解決していくという点でDQNが誕生したみたいですね。次回はDQNを組んでみようかなと思います。ではまた!