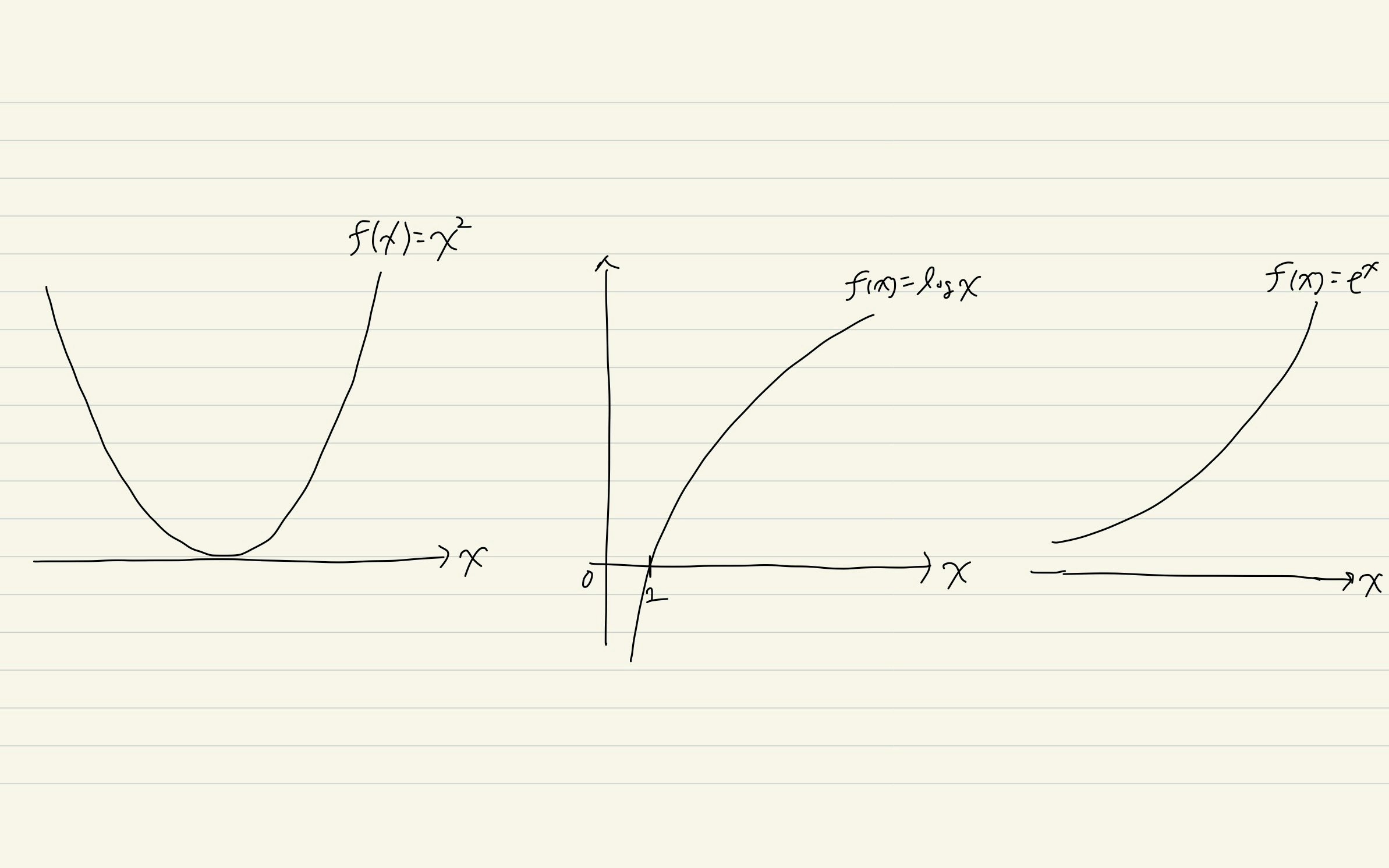わかった気になれるイェンセンの不等式 #数学

この記事は古川研究室 Advent_calendar 18日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。

はじめに

この記事では, イェンセンの不等式について解説します.

対象とする人

イェンセンの不等式について名前は聞いたことはあるけどよく知らない人.(例えば研究室の学部４年や修士１年)
イェンセンの不等式について勉強したい人.(おそらく研究室の学部４年や修士１年)

本記事の目的

この記事を読んだ人が以下の点を通してイェンセンの不等式について概観でき,かつ読者がイェンセンの不等式について「わかった気になれる」ことを目指します.

他概念との関係やどこで使われているかがわかる
イェンセンの不等式の数式とイメージが結びつく
イェンセンの不等式の証明ができる

0.準備:狭義凸関数・凸関数について

ここではイェンセンの不等式について理解するために必要な凸関数とは何かについて最低限述べます.凸関数について知ってるぜって人は読み飛ばして1.から読んでもらうといいかと思います.
凸関数とは一言で言うとある方向に膨らんでいる形をしている関数のことです.

0.1.定義

凸関数には大きく狭義凸関数と凸関数があり, それぞれ定義を確認します.
$f(x)$を開区間$I$¹上で定義された関数とします.

凸関数の定義

任意の$x_1,x_2 \in I$と$0 \leq \lambda \leq1$について以下の不等式を満たす時$f$を下に凸関数と呼ぶ.

f\left(\lambda x_{1}+(1-\lambda) x_{2}\right) \leq \lambda f\left(x_{1}\right)+(1-\lambda)f\left(x_{2}\right) \tag{1}

狭義凸関数の定義

任意の$x_1,x_2 \in I$(ただし$x_1\not=x_2$)と$0 < \lambda < 1$について以下の不等式を満たす時$f$を下に狭義凸関数と呼ぶ.

f\left(\lambda x_{1}+(1-\lambda) x_{2}\right) < \lambda f\left(x_{1}\right)+(1-\lambda)f\left(x_{2}\right) \tag{1}

※凸関数, 狭義凸関数それぞれ上に凸, 下に凸とありますが不等号が逆になるだけで本質的な違いはありません.また, 注意して欲しいのは線分と$f$が交わっている点は含まみません.

凸関数を図で書くと次のようなイメージです.

0.2.具体例

狭義凸関数の例

イメージとしては$f(x)$が定義されてるところにフラットなところや直線的な場所が全くない感じです.

$f(x)=x^{2}$($I=\mathbb{R}$)
$f(x)=\log x$($I=(0,\infty)$)
$f(x)=e^{x}$($I=\mathbb{R}$)

etc.

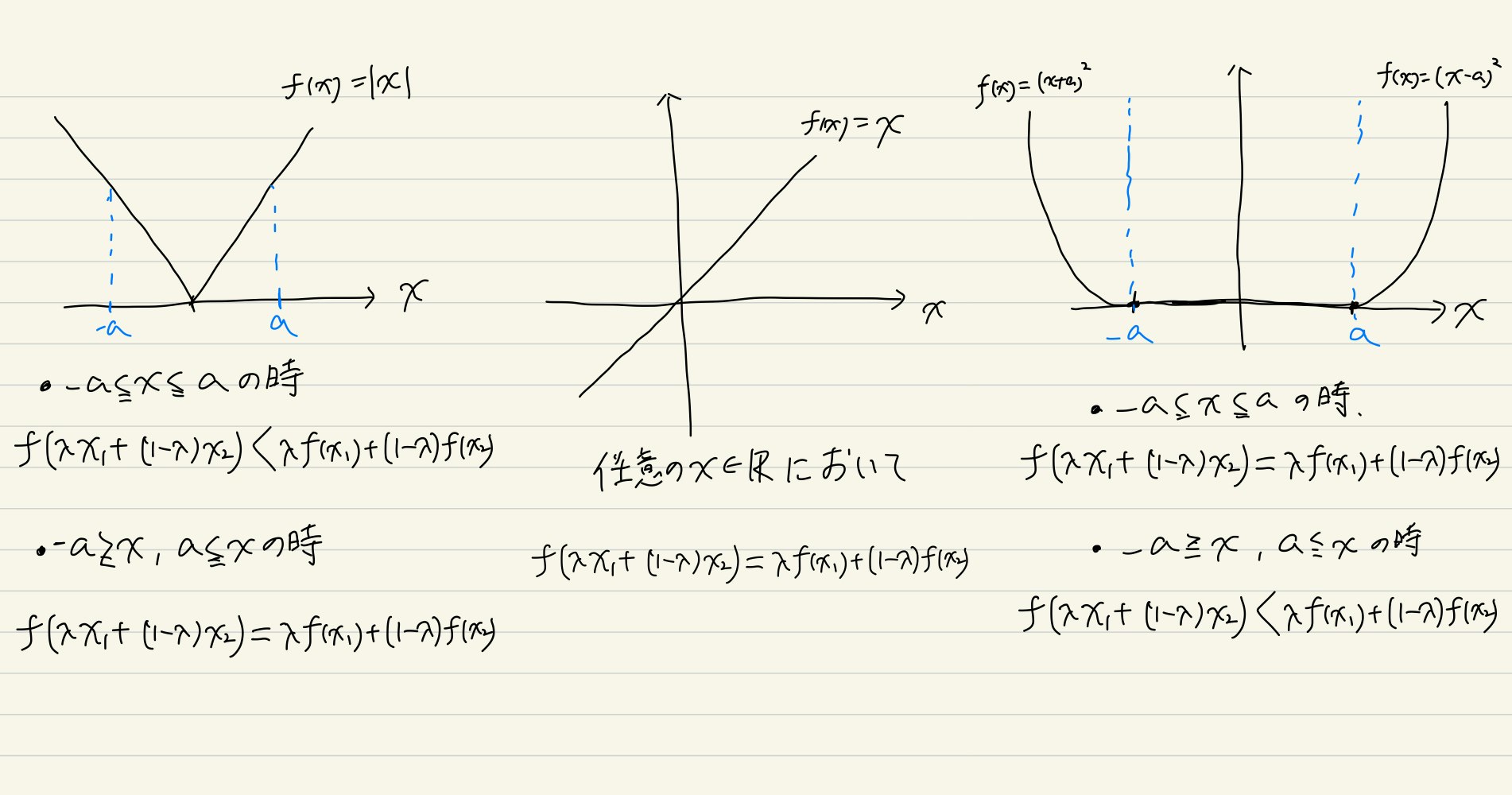
凸関数の例

狭義凸関数も凸関数に含むので狭義凸関数の具体例で出てきた関数も凸関数なのですが, 下にあげているのは狭義凸関数でないが凸関数である関数の例をあげています.狭義凸関数でないが凸関数である関数は区間的にフラットな部分や線形なところを作ればいくらでも作れます.

$f(x)=|x|$($I=\mathbb{R}$)
$f(x)=x $($I=(0,\infty)$)
$f(x)= \begin{cases} (x+a)^{2}・・・ x \leq -a \text{のとき} \\ 0・・・-a \leq x \leq a \text{のとき} \\ (x-a)^{2}・・・ x \geq a \text{のとき}\end{cases}$

etc.

1.イェンセンの不等式とは

1.1.概要

イェンセンの不等式とは,一言でいうと凸関数の定義の一般化です.具体的には以下の不等式になります.
等号成立に関しては後述します.

$f(x)$が下に凸の関数で, $x_1,x_2,...,x_n \in I$, $\lambda_1,...,\lambda_n$を$\sum_{k=1}^{n} \lambda_{k}=1$かつ$\lambda_k \geq 0$とする.この時に次のような不等式が成り立つ※1,※2.

\sum_{k=1}^{n}\lambda_{k}f(x_k) \geq f( \sum_{k=1}^{n} \lambda_{k}x_k)

※1上に凸の場合は不等式の向きが逆になります.$f(x)$が上に凸関数=$-f(x)$が下に凸関数なので, 以降は上に凸の関数も含めてこの書き方をします.
※2 「$f(x)$はイェンセンの不等式が成り立つ」 $\rightarrow$「$f(x)$は凸関数」という逆も言えます.つまり「$f(x)$は凸関数である」と「イェンセンの不等式が成り立つ」は同値関係にあります.

等号成立について

イェンセンの不等式で等号が成り立つというのは以下の式が成り立つことです.

\sum_{k=1}^{n}\lambda_{k}f(x_k) = f( \sum_{k=1}^{n} \lambda_{k}x_k)

どういう状況が考えられるかというと以下の状況が考えられます.
1. $x_1=x_2=...=x_n$のとき
2. $f(x)$が原点を通る直線のとき

1.は$x_1=x_2=...=x_n$となる点を$m$とすると$\sum_{k=1}^{n}\lambda_k=1$という条件を使うと等しいことを確かめることができます.
$f(x)$が狭義凸関数の場合等号の条件は1.しかありません.

\begin{align}
\text{(左辺)}=\sum_{k=1}^{n}\lambda_{k}f(m) = f(m)\\
\text{(右辺)}=f( \sum_{k=1}^{n} \lambda_{k}m)= f(m)
\end{align}

2.はイェンセンの等号成立の式は関数$f(x)$の線型性そのものです.この線型性が成り立つ関数は原点を通る直線などがあります.
$f(x)$が凸関数の場合は等号の条件は1.と2.両方考えられます.

1.2.どのようなところで使われるか？

大学入試

大学入試ではイェンセンの不等式について証明させる問題が出たり,イェンセンの不等式と関連する問題が出題されることがあります.²
また,イェンセンの不等式から相加相乗平均の関係, シュワルツの不等式などを導くことができます.³⁴

機械学習

機械学習の分野ではイェンセンの不等式を使って関数を不等式で評価することがよくあります.

機械学習では関数の最適化を行い最適なパラメータの推定を行います.しかし,解析的に計算できるものはごく限られています.解析的に取り扱えない関数を頑張って計算したい時にイェンセンの不等式で最適する関数を評価して計算できる形に持っていきます.具体的には$f(x)=logx$の場合⁵,$f(x)=x^{2}$の場合⁶⁷があります.
汎化誤差の評価を行う時にも使われます.⁸

情報理論

KL情報量の非負性を証明する時など, 情報理論における不等式を証明する時にもイェンセンの不等式を用いる場合があります.⁹

1.3.幾何学的なイメージ

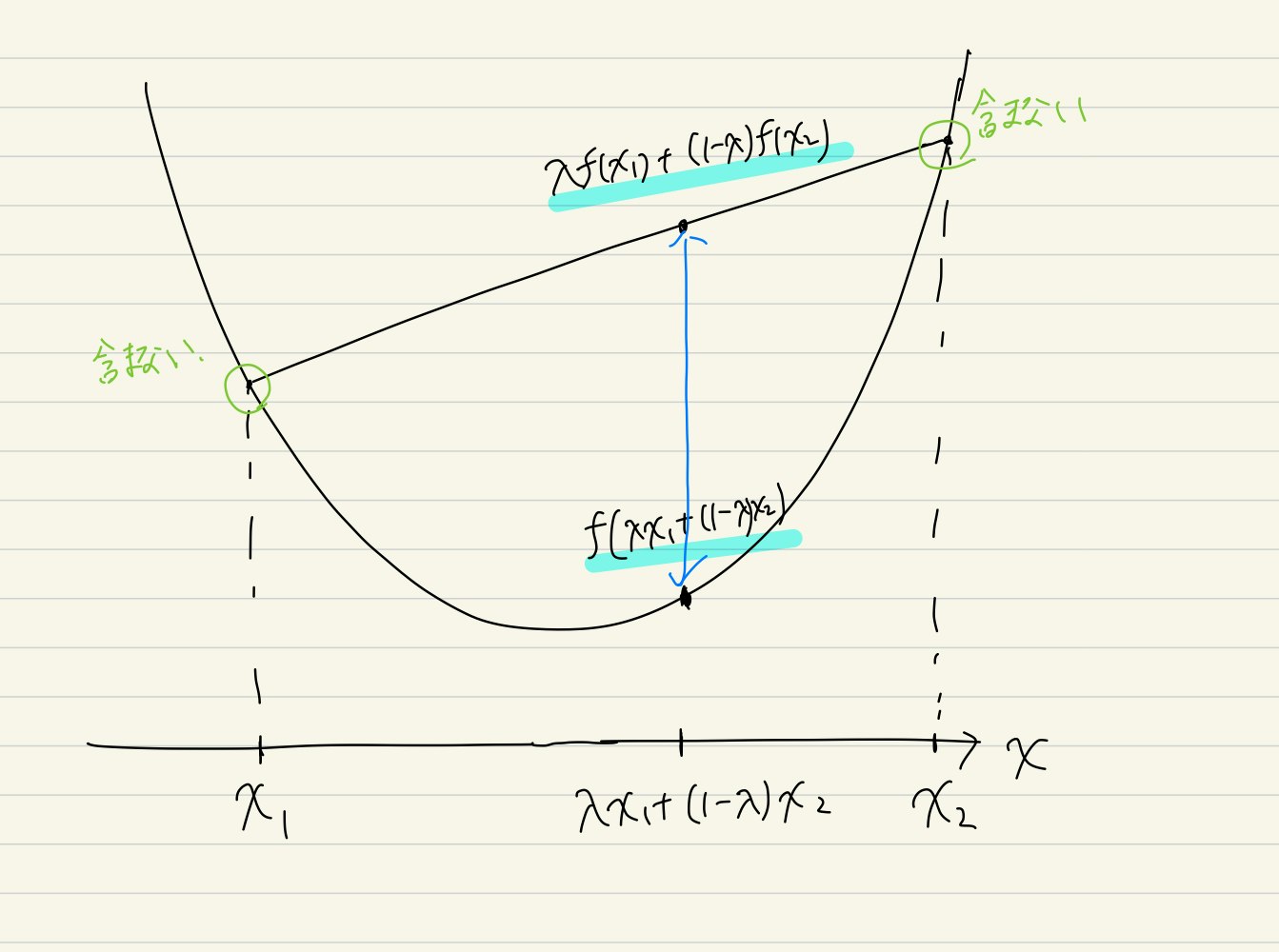
イェンセンの不等式のイメージとしては凸包（図で緑色で表した図形）が関数より上側にあることを意味しています.
またイェンセンの不等式の左辺は$\lambda_1=\lambda_2=...=\lambda_n=\frac{1}{n}$のときは$n$角形の重心になります.

n=2の時.凸関数の定義そのものです.
n=3の時.$\lambda_1f(x_1)+\lambda_2f(x_2)+(1-\lambda_1-\lambda_2)f(x_3)$を表す点が存在する範囲は色で塗った３角形のどこかです.$f(x)$と交わっているところは含みません。

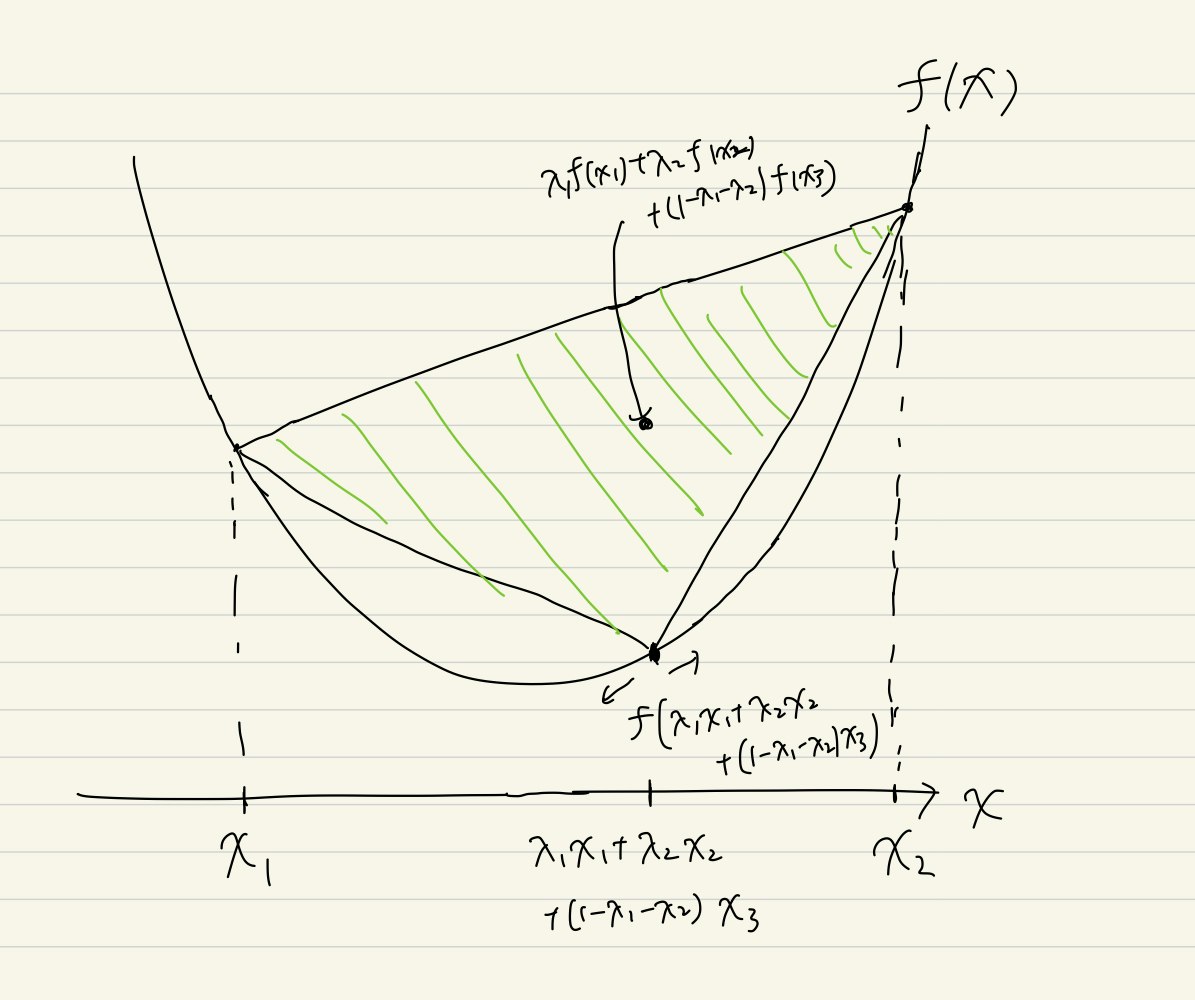
n=4の時.$\lambda_1f(x_1)+\lambda_2f(x_2)+(1-\lambda_1-\lambda_2)f(x_3)$を表す点が存在する範囲は色で塗った４角形のどこかです.$f(x)$と交わっているところは含みません。

2.イェンセンの不等式の証明

基本的に凸関数の性質を使って証明を行います.
証明する方法は様々あり, 数学的帰納法を使う方法, 接線を使う方法,幾何学的な性質を用いる方法, 平均値の定理を使った証明などがあります.
今回は, 数学的帰納法を使った証明と接線を使った証明を紹介します. 他は気が向いたら追記します.

2.1.数学的帰納法を使う方法

証明の方針

$f(x)$は凸関数なので凸関数の定義であるこの式をうまく使います.
ポイントとしては$n=k$のときこの式にうまく帰着させて示します.

f\left(\lambda x_{1}+(1-\lambda) x_{2}\right) \leq \lambda f\left(x_{1}\right)+(1-\lambda)f\left(x_{2}\right)

証明

[I] n=1の時.¹⁰

(左辺)=\lambda_1f(x_1)\\
(右辺)=f(\lambda_1x_1)\\
w1=1よりf(\lambda_1x_1)=f(x_1)\\
よって(左辺)=(右辺)となりn=1の時成立.

[II] n=2の時. $n=2$のときは$f(x)$は凸関数であり$\lambda_1+\lambda_2=1$なので凸関数の定義そのものである.よって成立.

f\left(\lambda_1 x_{1}+\lambda_2x_{2}\right) \leq \lambda_1 f\left(x_{1}\right)+\lambda_2f\left(x_{2}\right)

[III] $n=k$のとき成立すると仮定して$n=k+1$の時を示す.

$n=k$の時

\sum_{i=1}^{k}\lambda_{i}f(x_i) \geq f( \sum_{i=1}^{k} \lambda_{i}x_i)

$n=k+1$の時

(左辺)=\sum_{i=1}^{k+1}\lambda_{i}f(x_i)=\sum_{i=1}^{k}\lambda_{i}f(x_i)+\lambda_{k+1}f(x_{k+1}) \tag{4}

ここで$A=\sum_{i=1}^{k}\lambda_i$とする.式(4)を$A$を使って次のように式変形する¹¹

\begin{align}
& A\sum_{i=1}^{k}\frac{\lambda_{i}}{A}f(x_i)+\lambda_{k+1}f(x_{k+1})\\
& \geq A f(\sum_{i=1}^{k}\frac{\lambda_{i}}{A}x_{i})+\lambda_{k+1}f(x_{k+1}) \tag{5}
\end{align}

また,$\sum_{i=1}^{k+1}\lambda_i=\sum_{i=1}^{k}\lambda_{i}+\lambda_{k+1}=A+\lambda_{k+1}=1$であり, $f$は凸関数より式(5)は以下のように評価できる[^12]

\begin{align}
& \geq  f(A\sum_{i=1}^{k}\frac{\lambda_{i}}{A}x_{i}+\lambda_{k+1}x_{k+1})\\
& =f(\sum_{i=1}^{k+1}\lambda_{i}x_{i}) 
\end{align}

よって式(6)が成り立つ事、つまり$n=k+1$の時が成り立つ事が示せた.

\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \geq f( \sum_{i=1}^{k+1} \lambda_{i}x_i) \tag{6}

[I],[II],[III]より題意は示され, イェンセンの不等式が成り立つことが示せた.

2.2.接線を使う方法

$f(x)$は一階微分可能である事を前提とします.

証明の方針

凸関数の接線が関数の下側にあるということを使って証明します.¹²

証明

関数$f(x)$上の点$(\sum_{i=1}^{k+1}\lambda_{i}x_i,\sum_{i=1}^{k+1}\lambda_{i}f(x_i))$
の接線を$h(x)=f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i)$とする.

$f(x)$は凸関数より以下の関係が成り立つ.

f(x)\geq f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i)

また, 任意の点$x_1,...x_j,...,x_n$について以下の関係が成り立つ.

\begin{align}
f(x_1)& \geq f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_1-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \tag{a-1}\\
f(x_2)& \geq f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_2-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \tag{a-2}\\
  ...\\
f(x_n)& \geq f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_n-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \tag{a-n}
\end{align}

式(a-j)に対して$\lambda_j$(ただし$\lambda_{j}\geq 0$かつ$\sum_{j=1}^{n}\lambda_j=1$を満たす)を両辺に加える.

\begin{align}
\lambda_1f(x_1)& \geq \lambda_1f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_1-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \tag{b-1}\\
\lambda_2f(x_2)& \geq \lambda_2f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_2-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \tag{b-2}\\
  ...\\
\lambda_nf(x_n)& \geq \lambda_nf^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_n-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i) \tag{b-n}
\end{align}

式(b-1)から式(b-2)まで全て足すと以下の式になる.

\begin{align}
\sum_{j=1}^{n}\lambda_{j}f(x)& \geq \sum_{j=1}^{n}\lambda_{j}f^{\prime}(\sum_{i=1}^{k+1}\lambda_{i}x_i)(x_j-\sum_{i=1}^{k+1}\lambda_{i}x_i)+\sum_{i=1}^{k+1}\lambda_{i}f(x_i)\\
& =f(\sum_{i=1}^{k+1}\lambda_{i}x_i)
\end{align}

よって以下の関係が成り立つのでイェンセンの不等式が示せた.

\sum_{i=1}^{n}\lambda_{j}f(x) \geq f(\sum_{i=1}^{k+1}\lambda_{i}x_i)

3.確率論的観点からみたイェンセンの不等式

確率論的な観点からイェンセンの不等式をもう一度みてみたいと思います.

イェンセンの不等式(離散的な場合)

$p(x_k)$を離散確率分布とする.つまり$p(x_i) \geq 0$であり$\sum_{k=1}^{n}p(x_k)$である.¹³
また$x_1,...,x_n$を開区間$I$の任意の実数とする.$f$が凸関数の時, 以下の不等式が成り立つ.

\sum_{k=1}^{n}p_{k}f(x_k) \geq f( \sum_{k=1}^{n} p_k x_k)

これは前節で話したイェンセンの不等式と同じものを表してます.証明も同様にできます.

イェンセンの不等式(積分的な場合)

$x$を連続確率変数, $p(x)$を確率密度関数とする.また期待値$E[x]$を$E[x]=\int xp(x) dx$とする.
また$g(x)$を開区間$I$の可積分関数とする.¹⁴
$f$が凸関数の時, 以下の不等式が成り立つ.

\int p(x)f(g(x))dx \geq f( \int p(x)g(x)dx)

証明については, 本記事のイェンセンの不等式の証明の接線を使った方法を使って証明できます.

イェンセンの不等式の一般形

離散的な形や積分的な形を包含した一般的な書き方で書くことができます.
この形で覚えておくとイェンセンの不等式が使える場面に気づけるのでいいと思います.

確率変数を$x$,期待値を$E[x]$とする.この時$f$が下に凸の時次の関係が成り立つ.

E[f(x)] \geq f(E[x])

おわりに

間違いやわかりにくいところありましたら指摘していただけると嬉しいです

参考資料

筆者がイェンセンの不等式について勉強した時に参考にさせて頂いた書籍や記事になります.

$I$は関数$f(x)$の定義域のことです.例えば$I=(0,1)$とすると0と1を含まない0~1の実数区間を表します. ↩
このリンクにまとまっています.代表的な解析的不等式. ↩
http://shochandas.xsrv.jp/inequality/jensen.htm ↩
https://mathtrain.jp/holder ↩
EMアルゴリズム徹底解説 ↩
NMF（非負値行列因子分解）: 学習の可視化 ↩
非負値テンソル因子分解(NTF):学習の可視化 ↩
PACベイズの基礎についてまとめる ↩
対数和不等式の証明と応用 ↩
$n$=1の場合は自明なので$n$=2の時から始めてもいいと思います. ↩
数学的帰納法の証明のひらめきポイントはここです.$n=k$の条件を使いたいので$1=\frac{A}{A}$と式変形します.このように式変形すると$\sum_{i=1}^{k}\frac{\lambda_i}{A}=1$となり$n=k$の条件を使って不等式の評価ができます. ↩
本記事の内容とは関係ないですが凸関数と接線との関係を表しているものとしてルジャンドル変換というものがあります. ↩
$p(x_k)$は前節で述べた$\lambda_{k}$を表しています.確率分布ということを強調するためにあえて$p(x_k)$と書いています ↩
g(x)は前節で述べたx_1,...,x_nに対応します ↩