この記事は古川研究室 Advent_calendar 6日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
はじめに
NMFについて勉強したので出来るだけ分かりやすく解説していきます。
NMFとは何なのか?などNMFを初めて勉強する方の助けになれば幸いです(*^^)v
後半では学習の様子を可視化しています。
はじめに音楽の話をします。音楽は時間と共に周波数が変化します。ピアノやギター、トランペットなど様々な楽器が同時になってたりしますね...これらのデータは下のgif左側の行列で表現できます。このデータからピアノ、ギター、トランペット、それぞれの周波数と聞こえてくる時間をNMFを使うことで取得できます。ちなみにテンソルに対応したNTFってのもあります。→NTF学習の可視化
NMF(Non-negative Matrix Factorization)
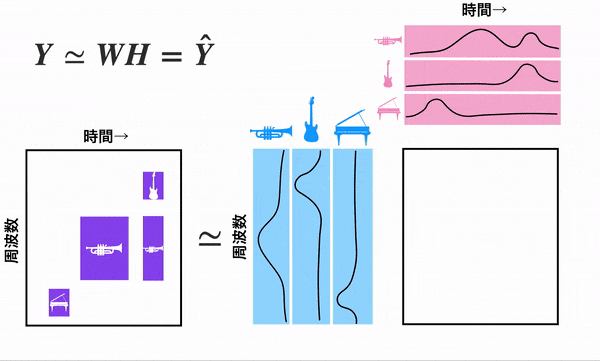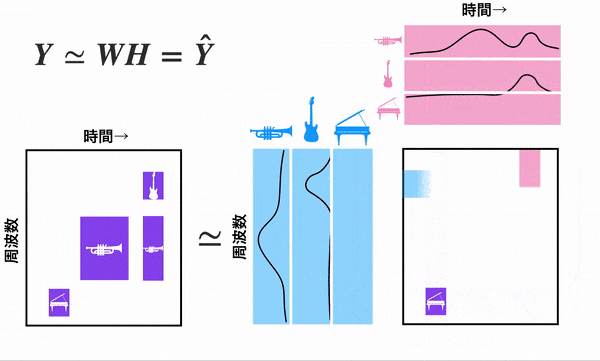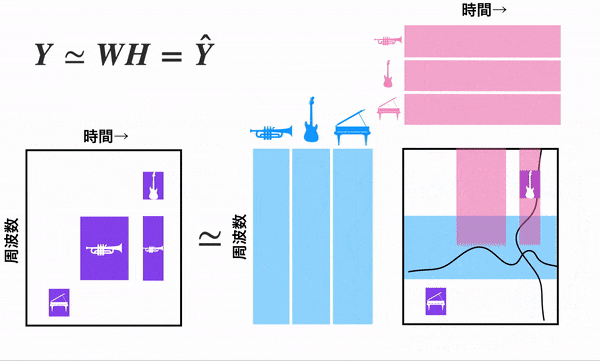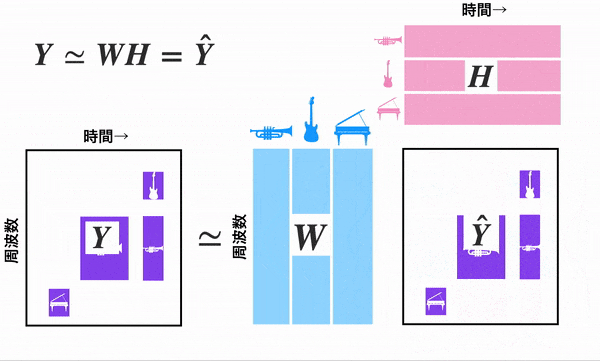
NMFでは非負制約条件下で行列$Y$を二つの非負値行列$W,H$に分解し近似します。つまり以下の図のようになります。
$$
y_{mn}\simeq\sum_{k} w_{m k} h_{k n}
$$
$$
\boldsymbol{Y} \simeq \boldsymbol{W} \boldsymbol{H}\boldsymbol{=} \boldsymbol{\hat{Y}}
$$
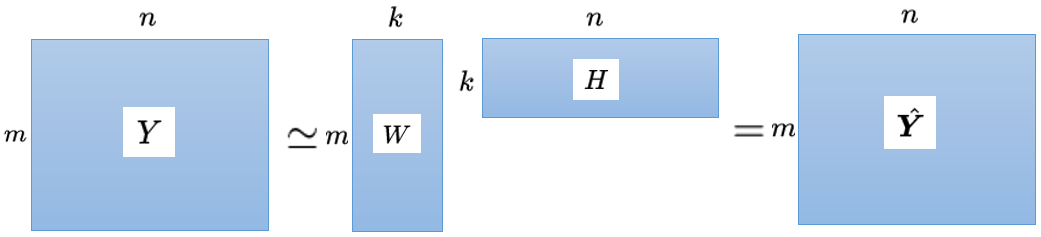
ポイントなのは行列 $Y,W,H,\hat{Y}$ が全て非負(マイナスな値がない)ことです。つまり$Y\geq0,W\geq0,H\geq0,\hat{Y}\geq0$です。NMFのアルゴリズムでは$W,H$の内積である$\hat{Y}$が出来るだけ元のデータである$Y$に近づくように$W,H$を更新していきます。更新式を求める際、解析的に計算困難な部分が出てきてしまうので、イェンセンの不等式を用いて式を置き換えます。更新式は最後に記載しています。(フロベニウスを用いた場合)
\begin{equation}
\begin{aligned}
D_{\mathrm{EU}}(\boldsymbol{W}, \boldsymbol{H}) &=\|\boldsymbol{Y}-\boldsymbol{W} \boldsymbol{H}\|_{F}^{2} \\
&=\sum_{m, n}\left|y_{m, n}-\sum_{k} w_{m, k} h_{k, n}\right|^{2}\\
&=\sum_{m, n}\left(\left|y_{m, n}\right|^{2}-2 x_{m, n} \sum_{k} w_{m, k} h_{k, n}+\underset{解析的に計算困難}{\left|\sum_{k} w_{m, k} h_{k, n}\right|^{2}}\right)
\end{aligned}
\end{equation}
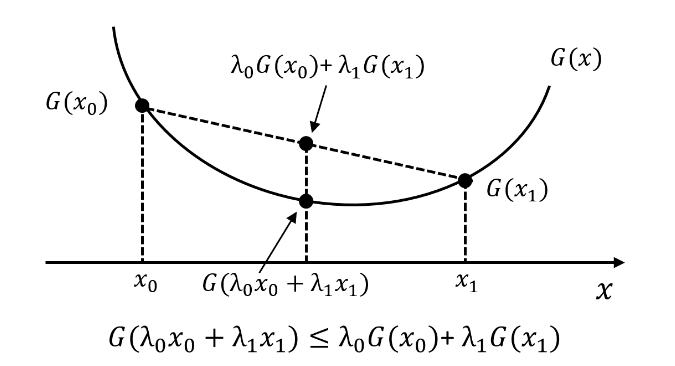
ここで計算困難な部分に対してイェンセンの不等式 $ G(\sum_{k=1} \lambda_{k} x_{k}) \leq \sum_{k=1} \lambda_{k} G(x_{k})$ (下図)を使い、式を置き換えます。$G(x)=x^2$ とすると不等式は$(\sum_{k=1} \lambda_{k} x_{k})^2 \leq \sum_{k=1} \lambda_{k} x_{k}^2$ となりますね。そして $ x_{k}=\frac{w_{m,k}h_{k,n}}{\lambda_{k}} $ と置くと不等式は$(\sum_{k=1} w_{m,k}h_{k,n})^2 \leq \sum_{k=1}\frac{w_{m,k}^2h_{k,n}^2}{\lambda_{k}}$ になります。不等式左辺は計算困難な式と一致してますので、右側の式に置き換えてあげましょう!
等号成立条件は$\lambda$が以下の時です。
\begin{equation}
\lambda_{k, m, n}=\frac{w_{m, k} h_{k, n}}{\sum_{k} w_{m, k} h_{k, n}}
\end{equation}
※ $\frac{w_{m,1}h_{1,n}}{\lambda_{1}}=\frac{w_{m,2}h_{2,n}}{\lambda_{2}},\lambda_{1}+\lambda_{2}=1$
この連立方程式を解くと等号成立条件も納得できます。
式を置き換えるとこうなりますね!
\begin{equation}
f:=\sum_{m, n}\left(\left|y_{m, n}\right|^{2}-2 y_{m, n} \sum_{k} w_{m, k} h_{k, n}+\sum_{k} \frac{w_{m, k}^{2} h_{k, n}^{2}}{\lambda_{k, m, n}}\right)
\end{equation}
これでようやく偏微分できますので
\begin{equation}
\frac{\partial f}{\partial w}=0,\frac{\partial f}{\partial h}=0
\end{equation}
偏微分して以下の2式を得る。以下の式を学習回数分繰り返すことで最適な$W,H$を求めます。
\begin{equation}
\begin{aligned}
w_{m k} \leftarrow w_{m k} \frac{(\boldsymbol{Y} \boldsymbol{H})_{m n}}{\left(\boldsymbol{W} \boldsymbol{H} \boldsymbol{H}^{T}\right)_{m k}}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
h_{k n} \leftarrow h_{k n} \frac{\left(\boldsymbol{W}^{T} \boldsymbol{Y}\right)_{m n}}{\left(\boldsymbol{W}^{T} \boldsymbol{W} \boldsymbol{H}\right)_{m n}}
\end{aligned}
\end{equation}
NMFの実装
2次元座標での実装
より理解を深めるためにNMFをpython実装していきましょう!
ここでは2次元座標をNMFで近似していきます。
左の図は一次関数にノイズを加えて80点プロットしたものになります。今回はこれを観測データ$Y$とします。
このデータ$Y$をNMFで分解し復元すると右図になります($\hat{Y}$)。うまく近似できていますね。
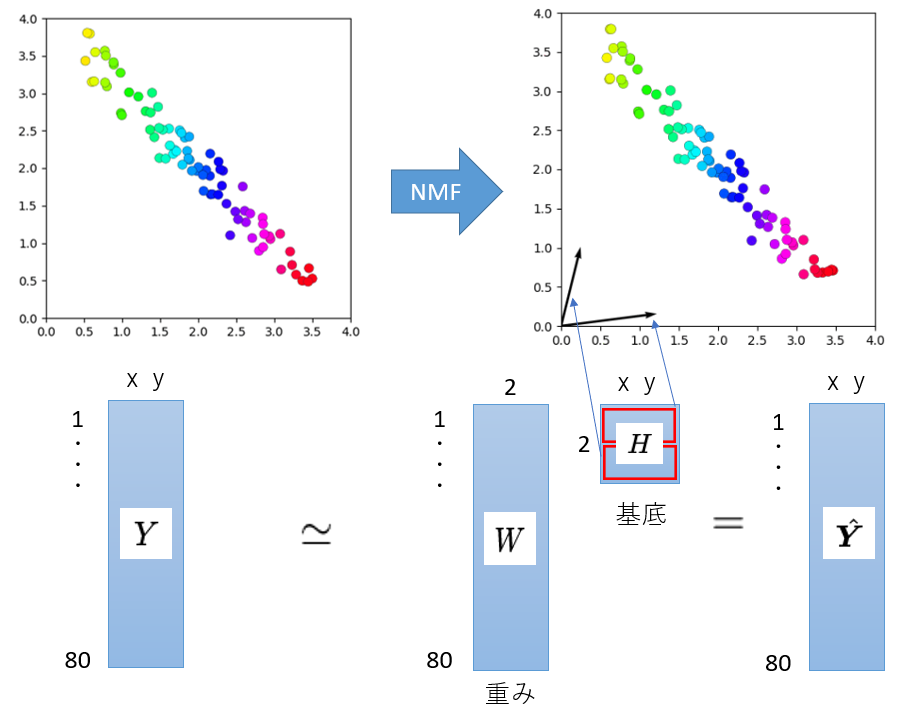
次に$W,H$について説明します。2次元座標において$W,H$は重みと基底ベクトルと解釈することができます。今回は$W$が重みで$H$が基底ベクトルと解釈できます。実際に基底ベクトルをプロットしたのが右図です。つまりデータ点はこの二つのベクトルの足し合わせで表現できます。
学習の様子
ここでは学習の様子を可視化していきます。可視化する意味あんの?
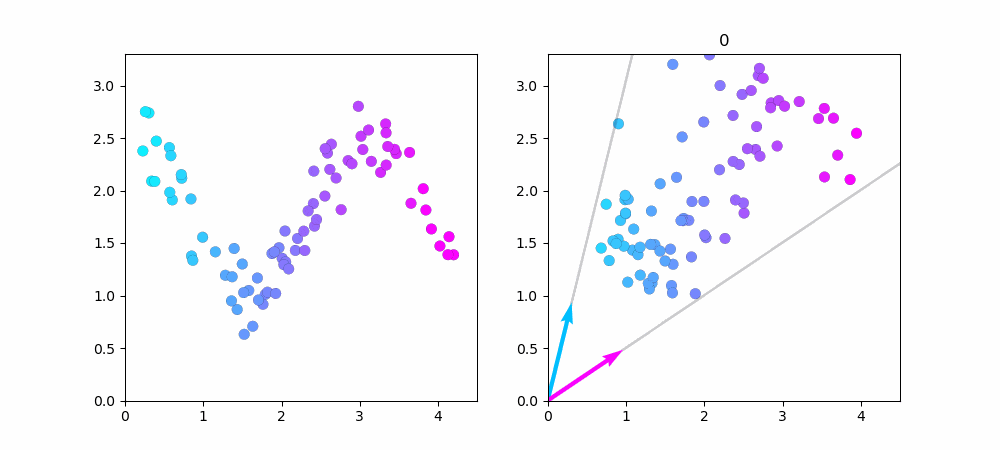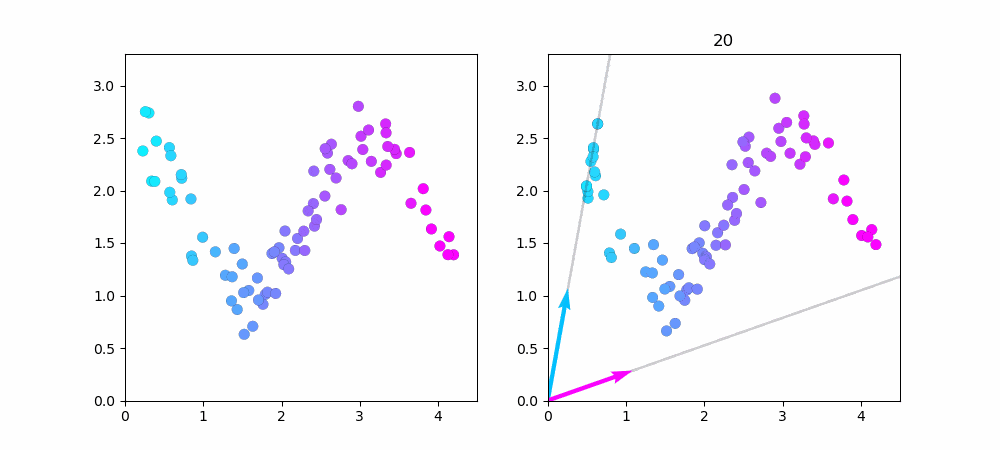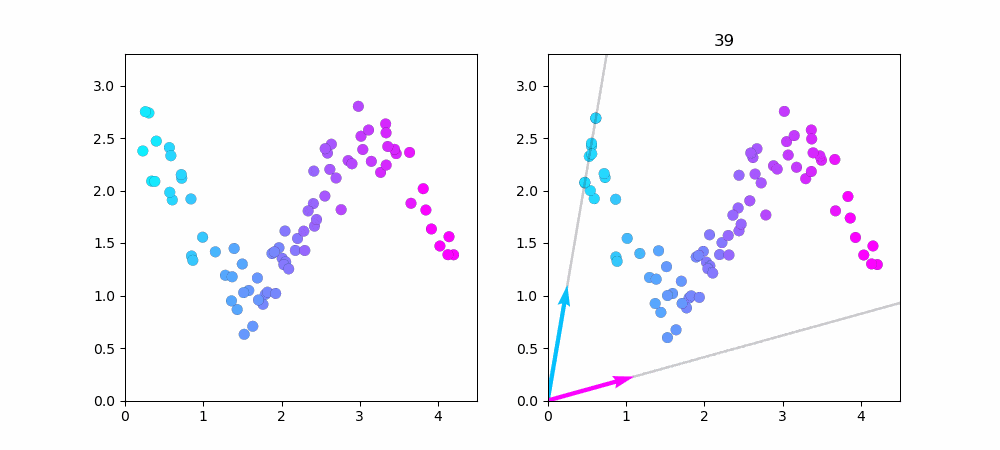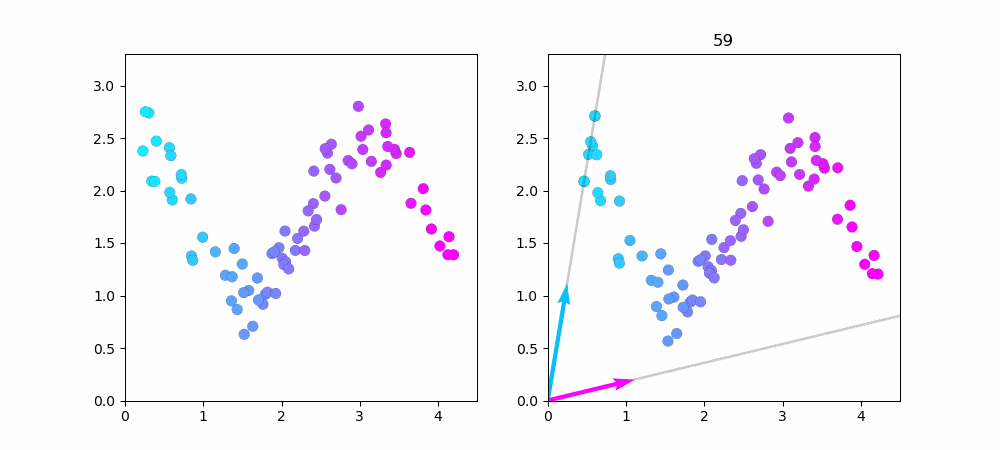
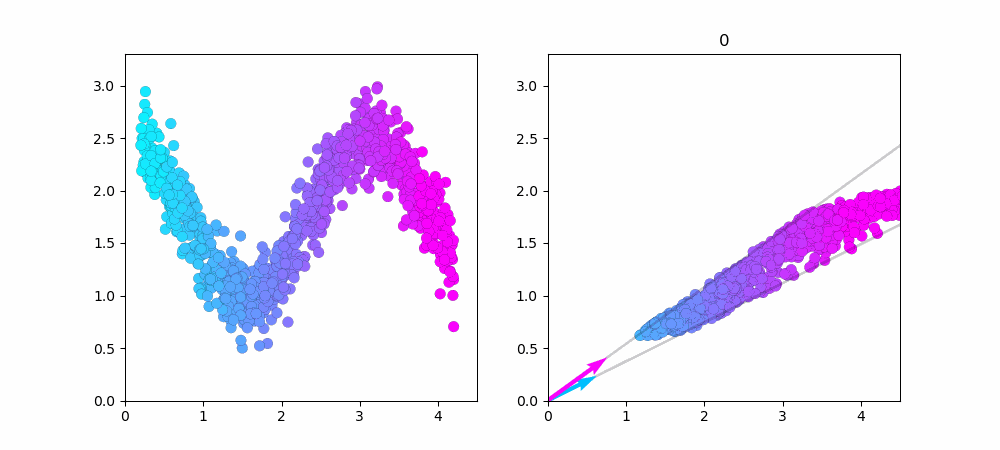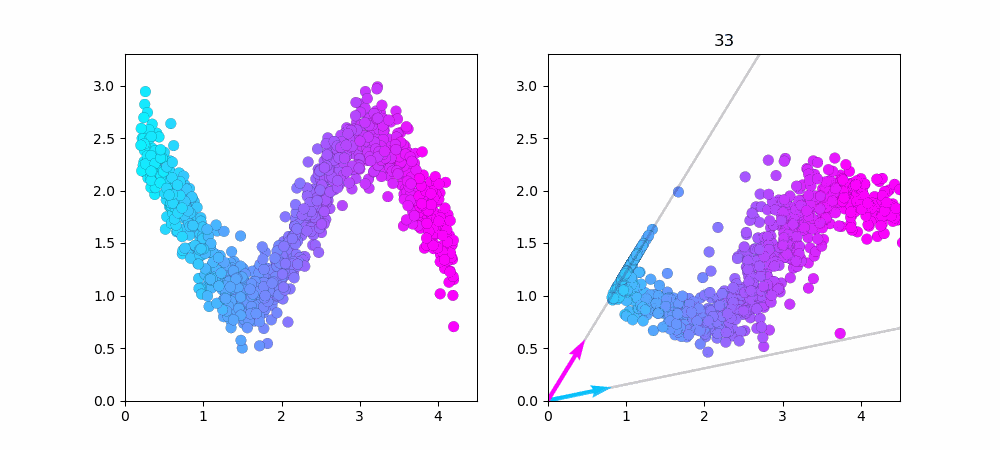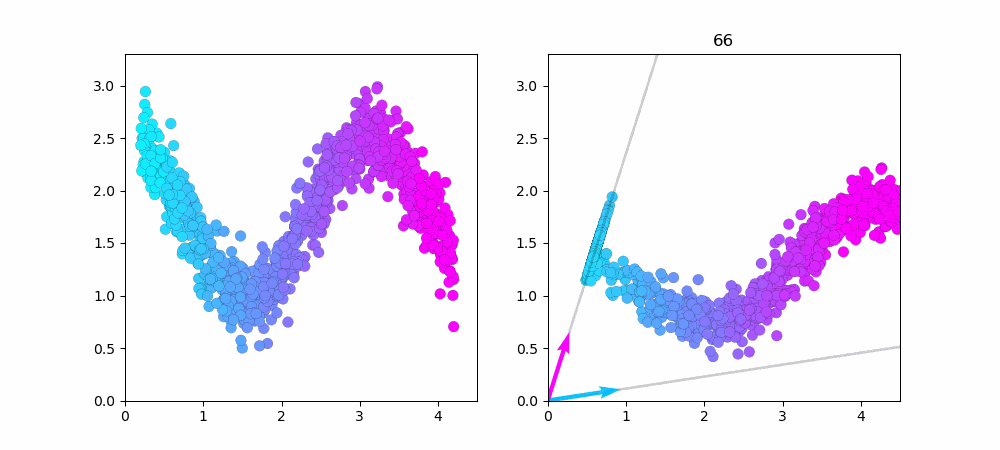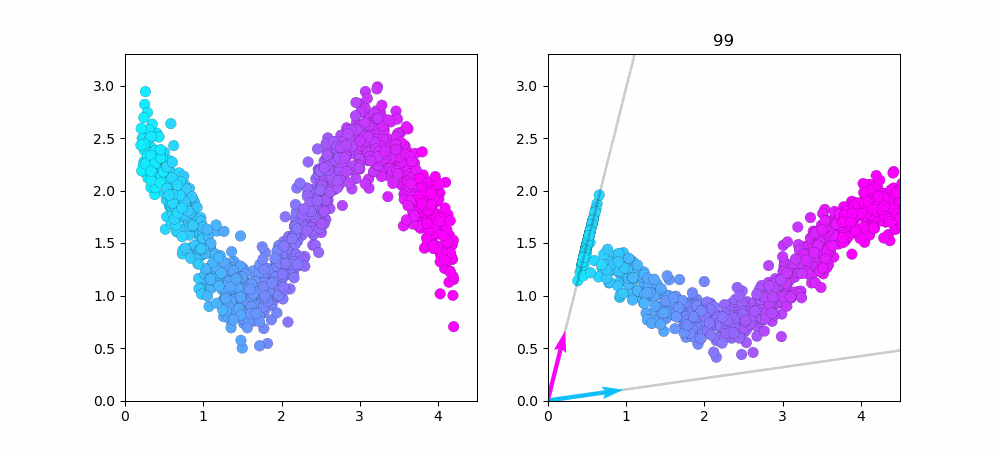
左図が$cos$関数で作ったデータ点です。右図がNMFで学習している様子です。
データ点を1000に増やしました。端っこの方がうまく近似できていないのが良く分かります。
水色のベクトルだけで近似できるデータ点は水色で、ピンク色のベクトルだけで近似できるデータ点はピンク色をしています。中心付近のデータは水色とピンク色のベクトル、両方を使っているので紫色(水色+ピンク=紫)になってますね...
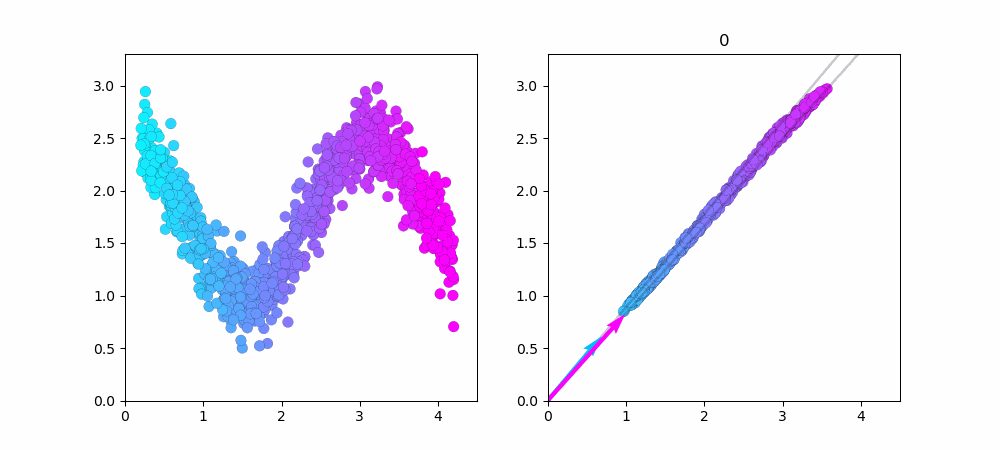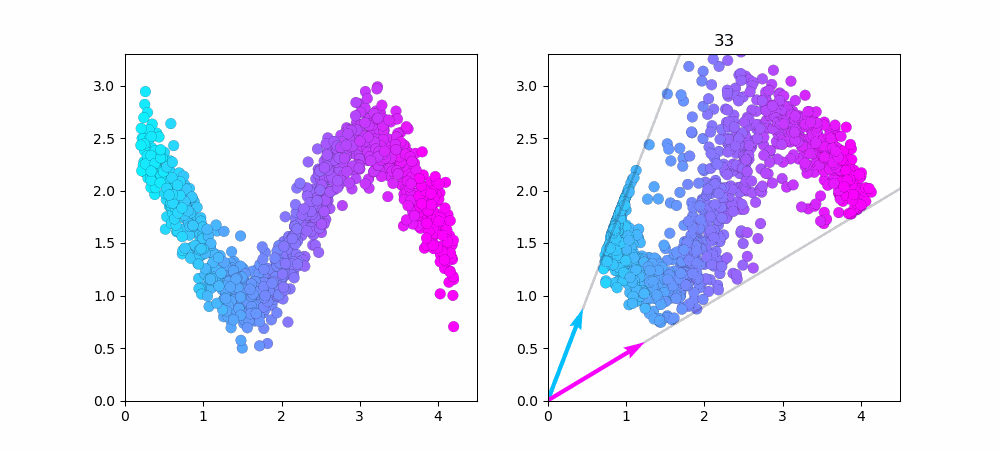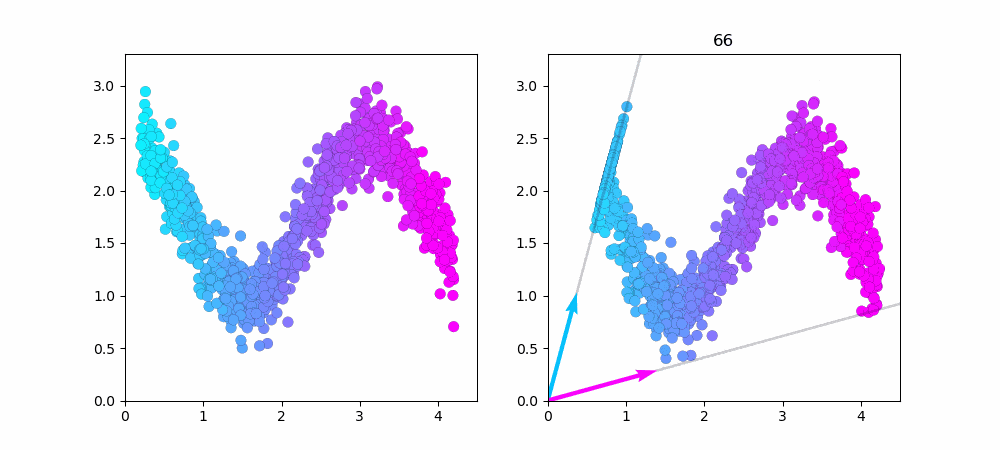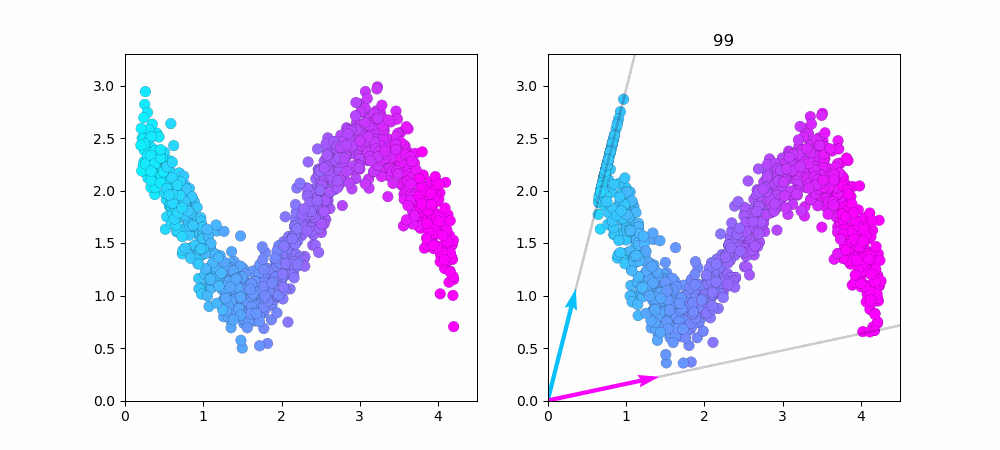
次に同じデータ数1000で、$W,H$の初期値を変えてみました...学習が上手くいっておらず元データをうまく近似出来ていません!このようにNMFでは$W,H$の初期値によって学習結果が変わります。
こちらは3次元のデータ点をNMFで近似した結果です。$k=3$だと$3$つのベクトルの足し合わせで元データを近似します。うまく出来ていますね。
一方、こちらは同じ3次元のデータですが、$k=2$としてます。2つのベクトルだと平面しか再現できないので上手く近似出来ていません。
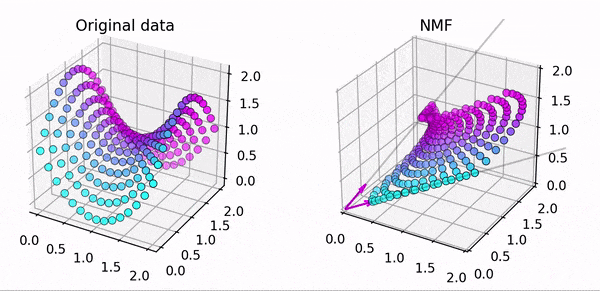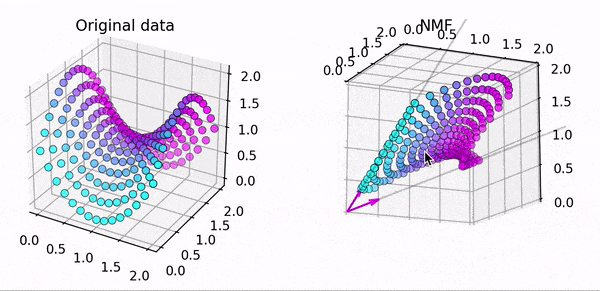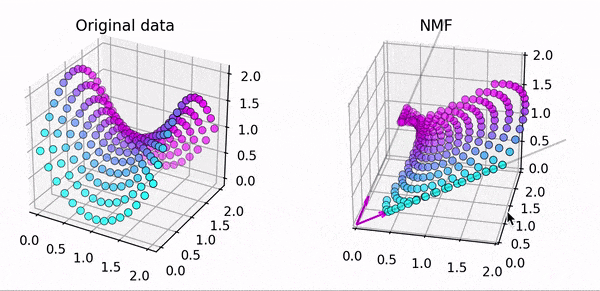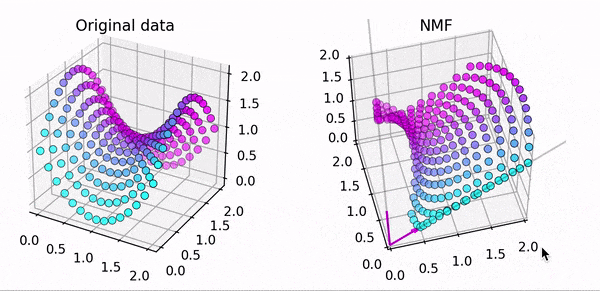
このようにNMFでは$W,H$の初期値および $k$ の数に注意する必要があります!
python code
アニメーションのコードになります。
# %matplotlib nbagg #jupyter用
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anm
import matplotlib.cm as cm
np.random.seed(32)
# cos関数
# 行列のサイズ指定
k = 2
m, n = 1000, 2
def true_fun(X):
return 1.5*np.cos(X)**2
# 観測データ用のデータ点作成(大分雑)
X=np.random.rand(m)*4+0.2
Y=true_fun(X)
Y=Y+np.random.normal(0,0.2,m)+1
x=np.zeros([m,2])
x[:,0]=X
x[:,1]=Y
# tは学習回数
t=0
vecter_x=0,0
vecter_y=0,0
# W,Hを作成
np.random.seed(91)
W = np.abs(np.random.uniform(low=0, high=1, size=(m, k)))
H = np.abs(np.random.uniform(low=0, high=1, size=(n, k)))
fig = plt.figure(figsize=(10,4.5))
def update(t):
# for t in range(100):
global W,H
# 更新式
W = W * np.dot(x, H) / np.dot(np.dot(W, H.T), H)
H = H * np.dot(W.T, x).T / np.dot(W.T, np.dot(W, H.T)).T
#復元
NMF = np.dot(W,H.T)
plt.subplot(122)
plt.cla()
plt.title(t)
plt.xlim((0, 4.5))
plt.ylim((0, 3.3))
plt.scatter(NMF[:,0], NMF[:,1],s=60,color=cm.cool((NMF[:,0]*0.25)),edgecolors='black',linewidths=0.1)
plt.quiver(0,0,H.T[1,0],H.T[1,1],angles='xy',scale_units='xy',scale=0.1,alpha=0.2)
plt.quiver(0,0,H.T[0,0],H.T[0,1],angles='xy',scale_units='xy',scale=0.1,alpha=0.2)
plt.quiver(0,0,H.T[1,0],H.T[1,1],angles='xy',scale_units='xy',scale=1.1,color='deepskyblue',width=0.012)
plt.quiver(0,0,H.T[0,0],H.T[0,1],angles='xy',scale_units='xy',scale=1.1,color='fuchsia',width=0.012)
plt.subplot(121)
plt.cla()
plt.xlim((0, 4.5))
plt.ylim((0, 3.3))
plt.scatter(X, Y,s=60,color=cm.cool((x[:,0]*0.25)),edgecolors='black',linewidths=0.1)
ani = anm.FuncAnimation(fig, update,interval = 300, frames = 100)
# ani.save('f333.gif',writer='pillow') #保存するときに使用
参考文献
[1] https://qiita.com/nozma/items/d8dafe4e938c43fb7ad1
[2] http://r9y9.github.io/blog/2013/07/27/nmf-euclid/
[3] https://qiita.com/mamika311/items/d920be626c343bcb423a
[4] https://qiita.com/sumita_v09/items/d22850f41257d07c45ea