非負値行列因子分解（NMF）をふわっと理解する

「Pythonではじめる機械学習」のp.152以降に非負値行列因子分解(NMF)の説明があるのだけれど、説明が素っ気なさ過ぎてよく分からず、かといってググってみても「実装はかんたんだよ！」という説明はたくさんあるもののやっぱりよく分からなくてモヤモヤしていたところ、スパース表現による音響信号処理(PDF)という資料を見つけて雰囲気はわかったような気がするのでちょっとメモっておく。

非負値行列因子分解(NMF: Nonnegative Matrix Factorization)

なにをやりたいのか

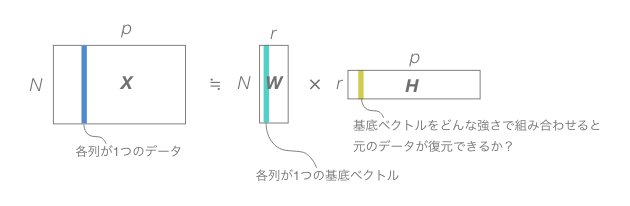
行列$X$を行列$W$と行列$H$の積で近似したい。

$$ X ≈ WH $$

ここで$X$は1つが$N$個の値からなる$p$個のデータをまとめて1つにしたような$N× p$行列で、これを分解するのだから$W$は$N$行でなければならないし、$H$は$p$列でなければならない。そして、$W$の列数=$H$の行数を$r$とすると、$W$の列として$r$個の基底ベクトルができる。

NMFのNMFたる所以は、$X$も$W$も$H$もそのすべての成分が非負であることを要求するという点にある。

なんで非負なの

世の中には非負の値で表現したほうが解釈しやすい情報がたくさんある。例えばピクセルの集合としての画像を考えると、各ピクセルの色をRGBなんかで表現するが、RもGもBも非負の数値で表現したほうが解釈しやすいだろう。負の画素値が何を意味するのかということを考えるのは難しい。

このあたりが「Pythonではじめる機械学習」だと省略されていたので、イメージがしにくかったような気がする。とにかく負の値を使うのは何かわかりにくくなりそうだから嫌だという強い気持ちが先にあったのだ（本当にそうなのかどうかは知らない）。

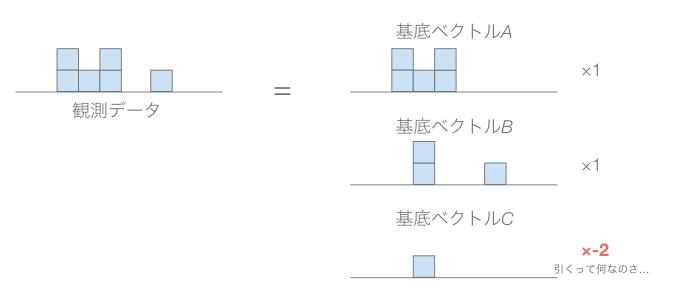
また、基底ベクトルと係数を非負に限定することで、係数が疎になりやすくなって理解しやすくなるらしい。このあたりは初めに示した資料の積み木っぽい図解が非常にわかりやすかったのでそのまま引用する。

係数に負を許すと、基底ベクトルを引いても良いということになる。これは積み木をマイナスに積み上げて高さを減らすと言っているようなもので、いかにも解釈が難しい。

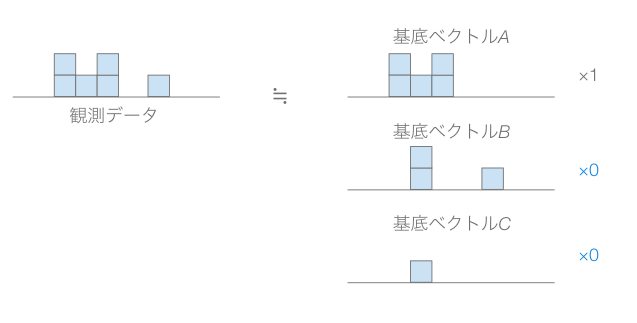
係数に負を許さないと、係数の意味はその基底ベクトルを使うという意味で一貫していて理解しやすい。また、もとのデータと共通部分が少ないような基底ベクトルは全く使わないという方向になりやすい（ここはまだ理解がふわっとしている）。

そして、係数を疎にするために各基底ベクトルはいくつかのデータの共通部分を抽出したようなものになりやすいということらしい（これも雰囲気は分かる気がするけどふわっとしている）。

どうやるのか

その話はまた今度な。

例で確認してみる

簡単なやつ

いきなり顔画像とかでやるから良くわからなくなるような気がするので、もっと単純な行列で試してみたい。scikit-learnだとsklearn.decomposition.NMFでNMFができるので、これを使ってみる。

{.python}

import numpy as np
from sklearn.decomposition import NMF

$X$としてはこんな感じのものを用意する。

{.python}

X = [
        [1, 1, 1, 0, 0, 0],
        [1, 1, 1, 0, 0, 0],
        [0, 0, 1, 1, 1, 0],
        [0, 0, 1, 1, 1, 0],
        [0, 0, 0, 1, 1, 1],
        [0, 0, 0, 1, 1, 1]
    ]

これを3つの基底ベクトルに分解すると、[1, 1, 1, 0, 0, 0]と[0, 0, 1, 1, 1, 0]と[0, 0, 0, 1, 1, 1]みたいなもの（がせいぜい定数倍されたもの）になってほしい。なるだろうか。

NMFを使うにはNMFクラスのインスタンスを生成して、fitメソッドを呼び出す。

{.python}

nmf = NMF(n_components=3)
nmf.fit(X)

$W$に相当するものは.transform(X)とやると得られる。$H$に相当するものは.components_に格納されている。

まずは$W$を確認する。

{.python}

W = nmf.fit_transform(X)
print(np.round(W, 1))

[[0.  1.2 0. ]
 [0.  1.2 0. ]
 [0.9 0.  0. ]
 [0.9 0.  0. ]
 [0.  0.  0.8]
 [0.  0.  0.8]]

いい感じっぽい。ついで$H$を確認する。

{.python}

H = nmf.components_
print(np.round(H, 1))

[[0.  0.  1.1 1.1 1.1 0. ]
 [0.9 0.9 0.9 0.  0.  0. ]
 [0.  0.  0.  1.3 1.3 1.3]]

$W$と$H$を掛けたら元の$X$が得られるはずだ。

{.python}

WH = np.dot(W, H)
print(np.round(WH, 1))

## [[1. 1. 1. 0. 0. 0.]
##  [1. 1. 1. 0. 0. 0.]
##  [0. 0. 1. 1. 1. 0.]
##  [0. 0. 1. 1. 1. 0.]
##  [0. 0. 0. 1. 1. 1.]
##  [0. 0. 0. 1. 1. 1.]]

うまくいった。でもこれは基底ベクトルから基底ベクトルを抽出したようなもので、だからどうした感がつよい。

ほんのり例を複雑にしてみる

共通部分を基底ベクトルとして抽出してくれるのなら、基底ベクトルを無作為に抽出して足し合わせて新しいデータを作成しても、もとの基底ベクトルをちゃんと抽出してくれるのでは…？

先程の$X$から無作為に重複ありで6つ抽出したものを足して新しいデータをつくる。1000セットほど。

{.python}

## pythonに慣れていないので非常に微妙なことをしている気がいたします
import pandas as pd
X_sample = []
df_X = pd.DataFrame(X)
for i in range(100):
    X_sample.append(np.array(df_X.sample(6, replace=True).sum()))
X_sample = np.array(X_sample)
print(X_sample[:10])

## [[3 3 5 3 3 1]
##  [3 3 6 3 3 0]
##  [2 2 2 4 4 4]
##  [2 2 3 4 4 3]
##  [3 3 3 3 3 3]
##  [3 3 4 3 3 2]
##  [1 1 4 5 5 2]
##  [3 3 4 3 3 2]
##  [2 2 5 4 4 1]
##  [3 3 4 3 3 2]]

これにNMFを使うと先ほどと同じように基底ベクトルが抽出できるはず…？

{.python}

nmf.fit(X_sample)
print(np.round(nmf.components_, 1))

## [[0.  0.  3.5 3.5 3.5 0. ]
##  [3.6 3.6 3.6 0.  0.  0. ]
##  [0.  0.  0.  4.6 4.6 4.6]]

うまくいった。