非負値テンソル因子分解(NTF):学習の可視化

この記事は古川研究室 Advent Calendar 10日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。

本記事を要約すると、これを実装します↓

#はじめに
本記事では非負値テンソル因子分解（NTF）の実装と式導出、学習の様子を可視化しています。NTFについて自分が勉強したことを皆さんと共有できればと思います。ちなみに非負値行列因子分解（NMF）についての記事も書いているので参考までにご覧いただけると幸いです。→NMF学習の可視化

#NTF : Non negative Tensor Factorization
非負値テンソル因子分解（NTF：Non negative Tensor Factorization）は非負値（マイナスの値がない）テンソルデータのパターンを抽出する手法であり、NMFの拡張手法です。NMFが行列（2階テンソル）を分解するのに対してNTFではテンソル（3階テンソルから）を分解します。

###更新式の導出
求めるテンソルデータを $x_{r,s,t}$ とし、3つの非負値行列を $u_{r,k},v_{s,k},w_{t,k}$ とします。そして今回は二乗誤差の場合の更新式を求めていきます。導出の流れはNMFと同じで、細かい計算はすっ飛ばしていますのでご了承下さい。

$F=\displaystyle\sum_{r}\displaystyle\sum_{s}\displaystyle\sum_{t}\big(x_{r,s,t}-\displaystyle\sum_{k}u_{r,k}v_{s,k}w_{t,k}\big)^2$
　$=\displaystyle\sum_{r}\displaystyle\sum_{s}\displaystyle\sum_{t}\big(|x_{r,s,t}|^2-2x_{r,s,t}(\displaystyle\sum_{k}u_{r,k}v_{s,k}w_{t,k})+\underset{\Large解析的計算困難}{\underline{|\displaystyle\sum_{k}u_{r,k}v_{s,k}w_{t,k}|^2}}\big)$

ここで解析困難な項が出てくるのでイェンセンの不等式を使って式を置き換えます。この辺の流れはNMFと同じです（参考）
$F\leq G=\displaystyle\sum_{r}\displaystyle\sum_{s}\displaystyle\sum_{t}\big(|x_{r,s,t}|^2-2x_{r,s,t}(\displaystyle\sum_{k}u_{r,k}v_{s,k}w_{t,k})+\underset{\Large置換部分}{\underline{\displaystyle\sum_{k}\lambda_{r,s,t,k}( \frac{u_{r,k}v_{s,k}w_{t,k}}{\lambda_{r,s,t,k}})^2}}\big)$
$※\lambda_{r,s,t,k}=\displaystyle\frac{u_{r,k}v_{s,k}w_{t,k}}{\sum_k{u_{r,k}v_{s,k}w_{t,k}}}$

こうすると偏微分可能になりますので微分していきます。

$\displaystyle\frac{\partial G}{\partial u_{r,k}}=\displaystyle\sum_{s}\displaystyle\sum_{t}\big(-2x_{r,s,t}v_{s,k}w_{t,k}+2\displaystyle\frac{u_{r,k}v_{s,k}^2w_{t,k}^2}{\lambda_{r,s,t,k}}\big)=0$

$\displaystyle\sum_{s}\displaystyle\sum_{t}x_{r,s,t}v_{s,k}w_{t,k}=\displaystyle\sum_{s}\displaystyle\sum_{t}\frac{v_{s,k}^2w_{t,k}^2}{\lambda_{r,s,t,k}}u_{r,k}$

$\lambda$に代入すると

$u_{r,k}=u_{r, k}\displaystyle\frac{\sum_s\sum_tx_{r,s,t}v_{s,k}w_{t,k}}{\sum_s\sum_tv_{s,k}w_{t,k}\sum_{k^{'}}u_{r,k'}v_{s,k'}w_{t,k'}}$

となります。これで$u_{r,k}$の更新式が求まりました。同じように
$\displaystyle\frac{\partial G}{\partial v_{s,k}},\displaystyle\frac{\partial G}{\partial w_{t,k}}=0$

を計算すると

$v_{s,k}=v_{s, k}\displaystyle\frac{\sum_s\sum_tx_{r,s,t}u_{r,k}w_{t,k}}{\sum_s\sum_tu_{r,k}w_{t,k}\sum_{k^{'}}u_{r,k'}v_{s,k'}w_{t,k'}}$

$w_{t,k}=w_{t, k}\displaystyle\frac{\sum_s\sum_tx_{r,s,t}v_{s,k}u_{r,k}}{\sum_s\sum_tv_{s,k}u_{s,k}\sum_{k^{'}}u_{r,k'}v_{s,k'}w_{t,k'}}$

これで全ての更新式が求まりました。あとは$u_{r,k},v_{s,k},w_{t,k}$を繰り返し計算するだけです。

#NTFの実装
それでは導出した式を使ってNTFを実装していきます。用意したテンソルデータは10×10×10の立方体形状にしました。（プロットする際は3次元にリシェイプしています）
参考文献として最後に論文のURLを載せていますが、その論文では更新式の導出方法が本記事とは異なります、更新式の形も異なっていますが、変形すると同じになります。※両方を実装すると計算結果も同じになりました。

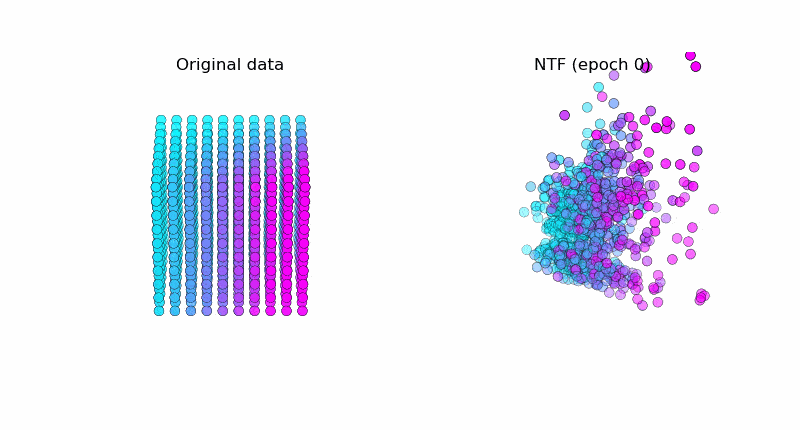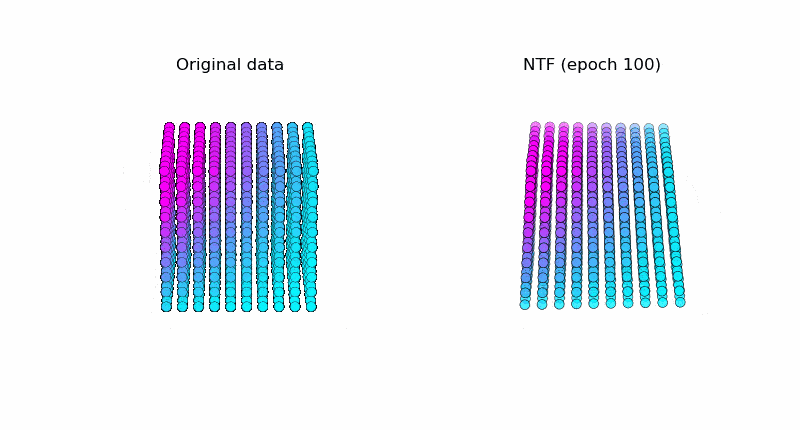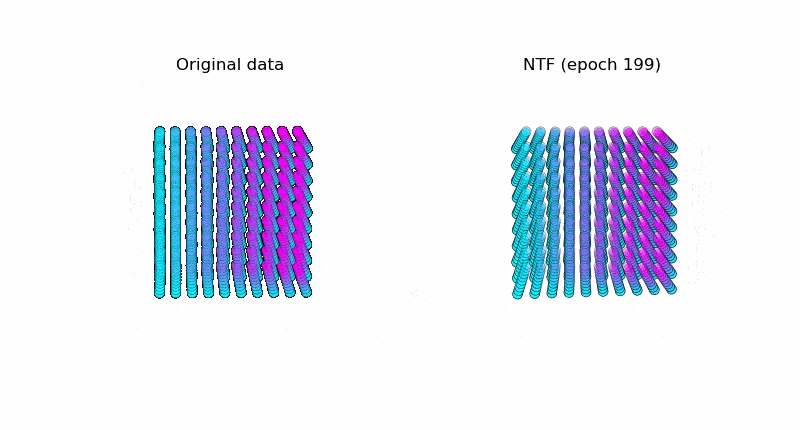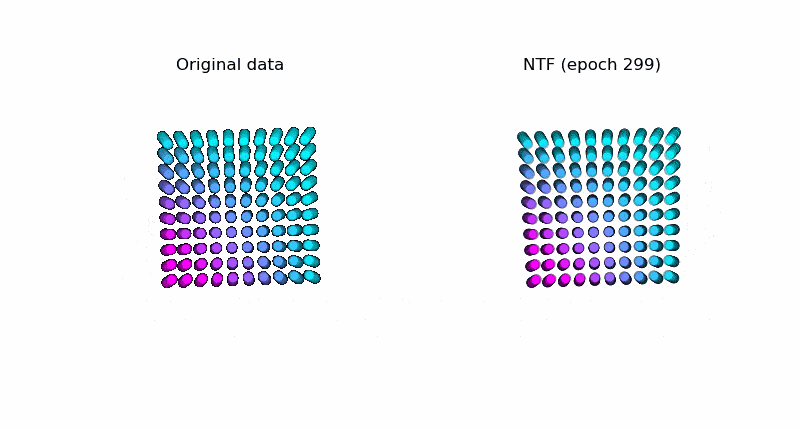
以下はNTFで元データ（図左）を復元している様子です。うまく元データを復元できています。※テンソルの値がどのように変化しているかを可視化しています ( $k=3$ )。

こちらは$k=2$とした場合です。うまく復元できていないのが分かります。

$k=1$とした場合です。これもうまく復元できていません、よってNMFと同様に$k$の数には注意が必要です。

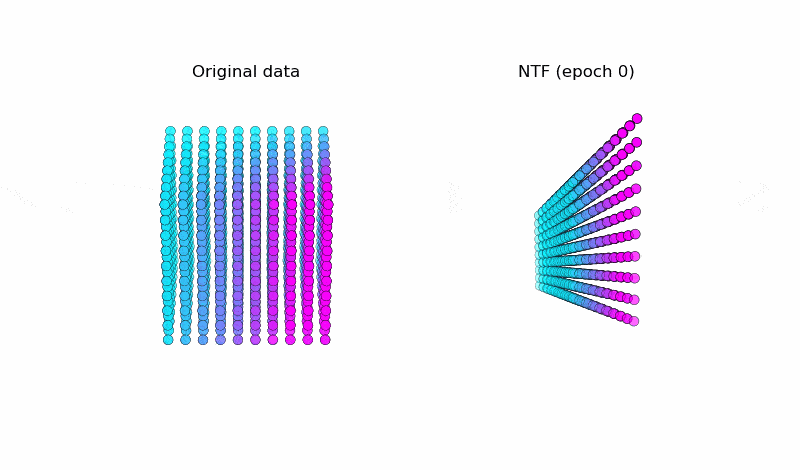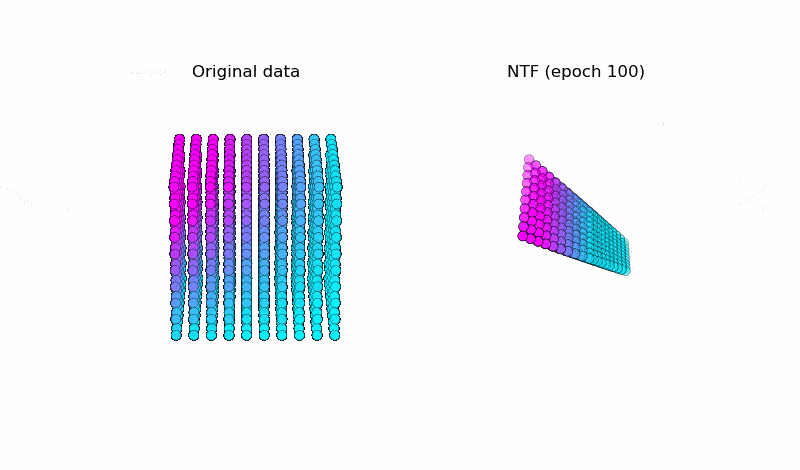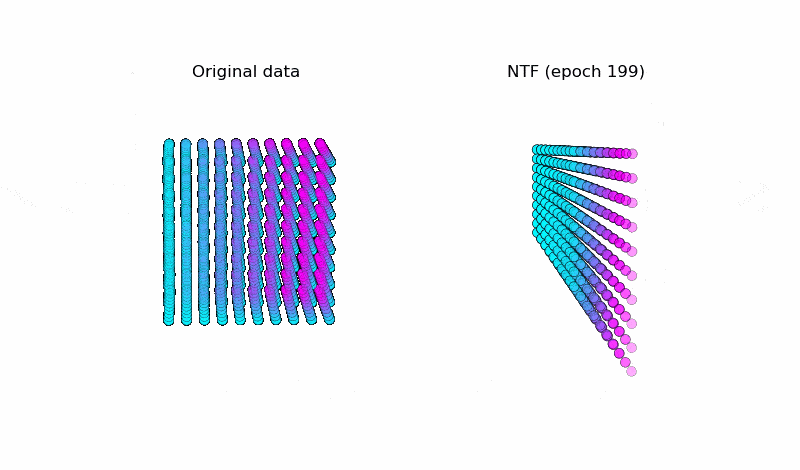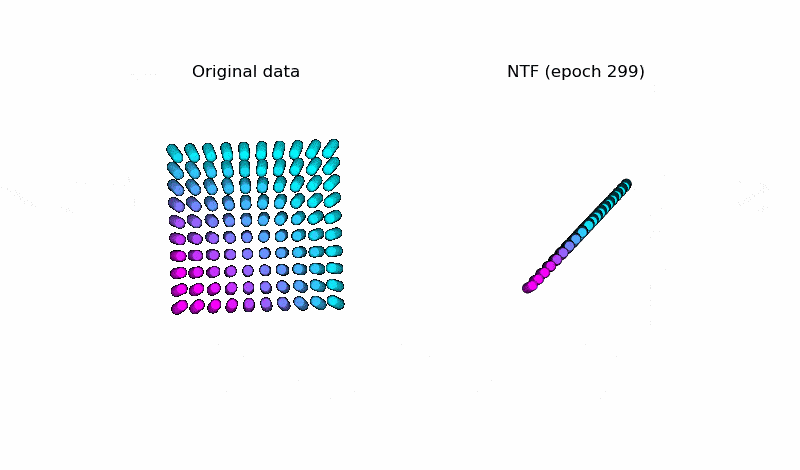
こちらがNTF実装のプログラムです（アニメーション）

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as anm
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import itertools

#tensor data の作成![Something went wrong]()
![Something went wrong]()

xx = np.linspace(1, 10, 10, endpoint=True)
X = np.array(list(itertools.product(xx, xx, xx)))
G=X.reshape(10,10,30)


#NTFの初期化
r=10
s=10
t=30
k=3
np.random.seed(2)
u=np.random.rand(r*k).reshape(r,k) 
v=np.random.rand(s*k).reshape(s,k) 
w=np.random.rand(t*k).reshape(t,k)  
u1,u2=u,u
v1,v2=v,v
w1,w2=w,w


fig = plt.figure(figsize=(12, 5.3))
ax_observable1 = fig.add_subplot(121, projection='3d')
ax_observable1.set_title('Original data')
ax_observable2 = fig.add_subplot(122, projection='3d')


def update(t):
    
    
    global deno_u,deno_v,deno_w,u1,v1,w1,U,u2,V,v2,W,w2,GG1,GG2
    # 参考論文の更新式
    deno_u = np.einsum('rm,mj->rj',u1,np.dot(v1.T,v1)*np.dot(w1.T,w1))
    u1=u1*np.einsum('ijt,jk,tk->ik',G,v1,w1)/deno_u
    deno_v = np.einsum('sm,mj->sj',v1,np.dot(u1.T,u1)*np.dot(w1.T,w1))
    v1=v1*np.einsum('ijt,ik,tk->jk',G,u1,w1)/deno_v
    deno_w = np.einsum('tm,mj->tj',w1,np.dot(u1.T,u1)*np.dot(v1.T,v1))
    w1=w1*np.einsum('rst,rk,sk->tk',G,u1,v1)/deno_w
    
    #NMFの延長で導いた式
    U=np.einsum('ik,jk,lk->ijl',u2,v2,w2)
    u2=u2*np.einsum('ijl,jk,lk->ik',G,v2,w2)/np.einsum('jk,lk,ijl->ik',v2,w2,U)
    V=np.einsum('ik,jk,lk->ijl',u2,v2,w2)
    v2=v2*np.einsum('ijl,ik,lk->jk',G,u2,w2)/np.einsum('ik,lk,ijl->jk',u2,w2,V)
    W=np.einsum('ik,jk,lk->ijl',u2,v2,w2)
    w2=w2*np.einsum('ijl,ik,jk->lk',G,u2,v2)/np.einsum('ik,jk,ijl->lk',u2,v2,W)
    
    #復元
    GG1=np.einsum('ik,jk,tk->ijt',u1,v1,w1)
    GG2=np.einsum('ik,jk,lk->ijl',u2,v2,w2)
  
    GG1=GG1.reshape(1000,3)
    GG2=GG2.reshape(1000,3)
    
    #元データのプロット
    plt.cla()
    ax_observable1.scatter(X[:, 0], X[:, 1], X[:, 2],s=50,edgecolors='black',linewidths=0.1,color=cm.cool(X[:,1]*np.linspace(0, 0.13, 1000))) #edgecolors="b"
    ax_observable1.set_xlim(0,11.5)
    ax_observable1.set_ylim(0,11.5)
    ax_observable1.set_zlim(0,11.5)
    ax_observable1.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax_observable1.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0)) 
    ax_observable1.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0)) 
    #ax_observable1.view_init(elev=30+t*0.8, azim=3.6*-t*0.5) #回転用
    ax_observable1.grid(False)
    
    #近似結果のプロット
    
    ax_observable2.scatter(GG2[:,0],GG2[:,1],GG2[:,2],s=50,edgecolors='black',linewidths=0.1,color=cm.cool(X[:,1]*np.linspace(0, 0.13, 1000))) 
    ax_observable2.set_xlim(0,11.5)
    ax_observable2.set_ylim(0,11.5)
    ax_observable2.set_zlim(0,11.5)
    ax_observable2.set_title("NTF (epoch "+str(t)+")")
    ax_observable2.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax_observable2.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0)) 
    ax_observable2.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    #ax_observable2.view_init(elev=30+t*0.8, azim=3.6*-t*0.5) #回転用
    ax_observable2.grid(False)
    
    

ani = anm.FuncAnimation(fig, update,interval = 50, frames = 180)
#ani.save('NTF.gif',writer='pillow') #gif保存用

#参考文献
NTFの更新式が乗ってる論文です。
Sparse Image Coding using a 3D Non-negative Tensor Factorization