ベイズ線形回帰で更に実践的な分析へ ~pyroによる実装例~

はじめに

線形回帰は解釈性も高く、パラメータ推定も容易なので非常に協力な手法です。
また、一般化線形回帰へ拡張することで、より多様なデータにも適用することができるため、現在でも様々な場面で利用されています。
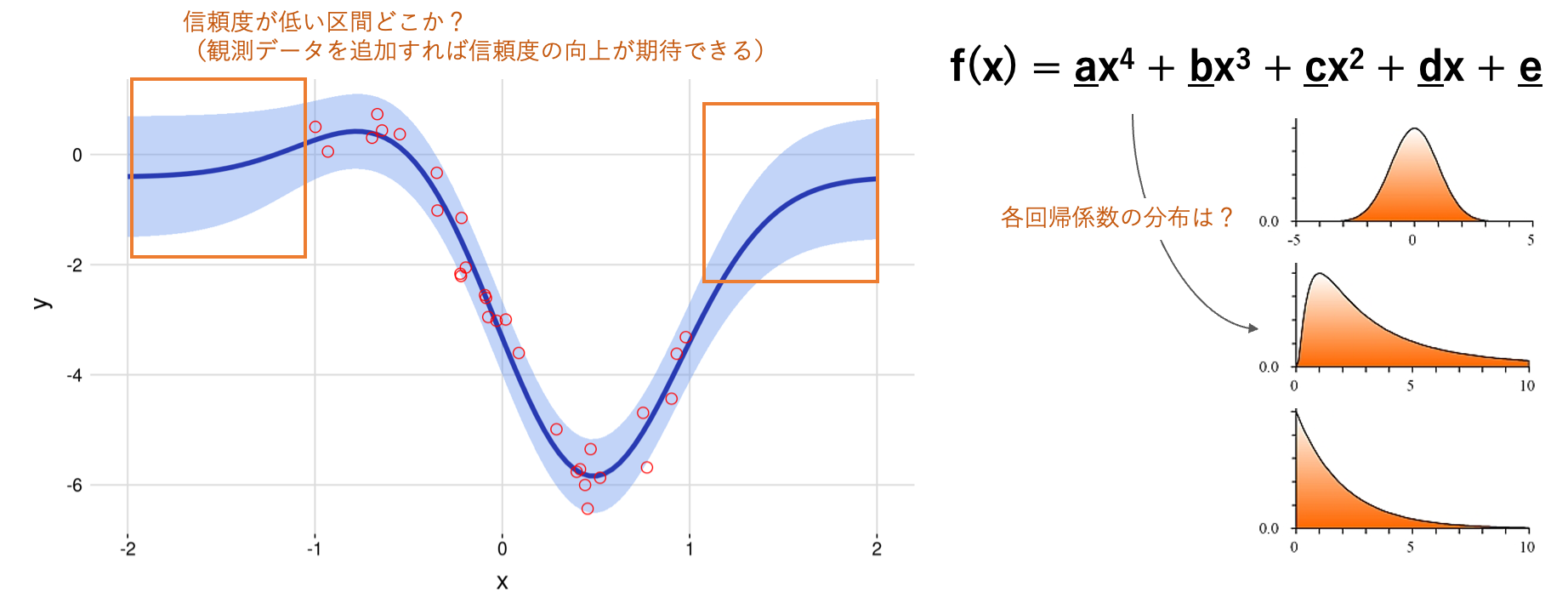
一方で、線形回帰を使っていると、以下の様な疑問に直面することはないでしょうか？

• パラメータ（回帰係数）はどの程度、信頼できるのか？
• 予測結果はどの程度信頼できるのか？
• より精度をあげるために追加データの取得を考えているが、どの範囲で追加取得するのがいいのか？
  

線形回帰を行う主なモチベーションの一つにパラメータ（回帰係数）の解釈があるかと思います（予測精度だけを追及するならブラックボックスMLで良い）。
しかし、点推定だけの解釈は危険あり、その背後にある分布も捉えることでより正しい理解につながります
（例えば、目的変数に対して大きな値を示していても、非常に分散が大きい場合は信頼できなかったり、分布が正規分布していない場合は、その平均値を代表値として解釈することは問題がある）
また、一般にデータの追加取得にはコストがかかるので、より信頼度が低い範囲のデータを集中的に取得できると効率的だと思います。
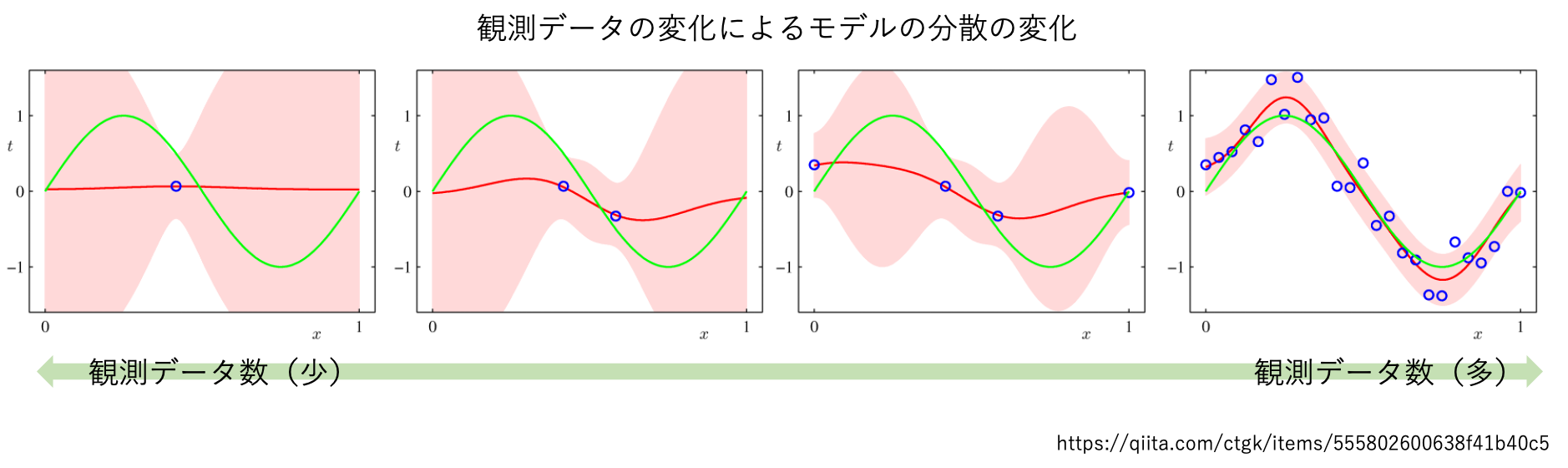
ベイズ曲線フィッティングの記事では、観測データが少ないところでは分散が大きくなり、観測データが増えるにつれて追加取得箇所の分散が減少する実験を確認できます。

そこで、今回は線形回帰をベイズ拡張することで、上記の疑問に答えられる分析を紹介たいと思います。
ここでは、pyroという確率的プログラミング言語を利用します。
pyroの基本的な使い方や他の確率的プログラミング言語の紹介ははこちらの記事を参照ください。

pyroによるベイジアンモデリング

pyroでは事後分布の近似推論をする方法として、変分推論とMCMCによる解法がサポートされています。

• 変分推論: 最適化に基づく推論（近似分布と事後分布との差を最小化）
• MCMC: サンプリングに基づく推論
  理論面の解説は様々な記事がネット上にあるので、それらを参照ください。
  使い分けとしては一般に、MCMCは遅いが推定品質がよく、変分推論は早いが漸近的に分布の保証がない点が言われています。

pyroはpytorchをベースにしているため大規模データに対してはGPUを用いることで高速化することが可能です。
こちらの記事のGoogle colabによる実験では、サンプル数が10万を超えるあたりからGPUの強みが出てくるそうです。
本記事は変分推論による利用方法を中心にベイズ線形回帰を紹介していきます（MCMCによる推定もほぼ同じ方法です）

実装手順

はじめに、pyroによる変分推論の実装手順を整理しました。

• モデル定義
  • モデルの表現に必要なパラメータや回帰式の形を定義します
  • 事前に仮定する分布の形状やノイズの大きさを設定できます
• ガイド定義
  • 変分推論を行うために必要な近似事後分布を設定します
  • pyroに自動設定してもらう方法と手動で近似事後分布を設定する方法があります
  • 手動で設定する場合はモデル定義内のパラメータ名とガイド内のパラメータ名を一致させる必要があります
• 推論実行
  • 最適化手法と損失関数を設定して推論を実行します（pytorchと類似）
  • infer.SVIにmodel, guide, optimizer, lossを渡して、svi.stepで更新すれば学習が進みます
• 予測（事後分布のサンプリング)
  • 学習したモデルから事後分布をサンプリングします
  • num_sampleでサンプリングするデータ数を指定することができます
  • 構築した予測モデルに予測値が欲しい区間の説明変数を入力すると、目的変数のサンプリング結果が　返ってきます

次章では実際にサンプルデータを用いて、上記の手順を実行するデモを紹介します。

ベイズ線形回帰（デモ）

• 本デモでは、以下の条件でベイズ推論を行います
• 推定したいモデル
  • ２つのパラメータw_0とw_1からなる線形結合モデル
  • モデルの出力 y (= w_0 + w_1*x )にノイズ（σ=0.3）が乗ったものを考える

w_0 \sim  {\rm Normal} (1.0, 1) \\
w_1 \sim  {\rm Normal} (0.4, 1) \\
y\sim  {\rm Normal} (w_0 + w_1*x, 0.3)\\

• 事前分布

w _ 0 \sim  {\rm Normal} (0, 10)\\
w _ 1 \sim  {\rm Normal} (0, 10)\\
y\sim {\rm Normal}(w _ 0 + w _ 1 x, 1)

インストール

• pyroのインストールにはpytorchもインストールする必要があります

conda install pytorch torchvision torchaudio -c pytorch
conda install -c conda-forge pyro-ppl 

ライブラリインポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
from torch import nn

import pyro
from pyro import distributions as dist
import pyro.infer as infer
from torch.distributions import constraints

サンプルデータの作成

• 適当なサンプルデータを作成します
• pyroはpytorchのtorch型で扱う必要があるのでデータ型を変換をしておきます

# サンプルデータの作成

## 推定したい真のモデル
def truth_func(x, beta_0, beta_1):
    y = beta_0 + beta_1 * x + 0.3 * np.random.randn(len(x))
    return y

x = np.random.uniform(low=0.0, high=1, size=1000)
y = truth_func(x, beta_0=1, beta_1=4)

# numpyからtoech.tensor型へ変換
x = torch.tensor(x)
y = torch.tensor(y)

# 可視化
plt.plot(x, y, ".")

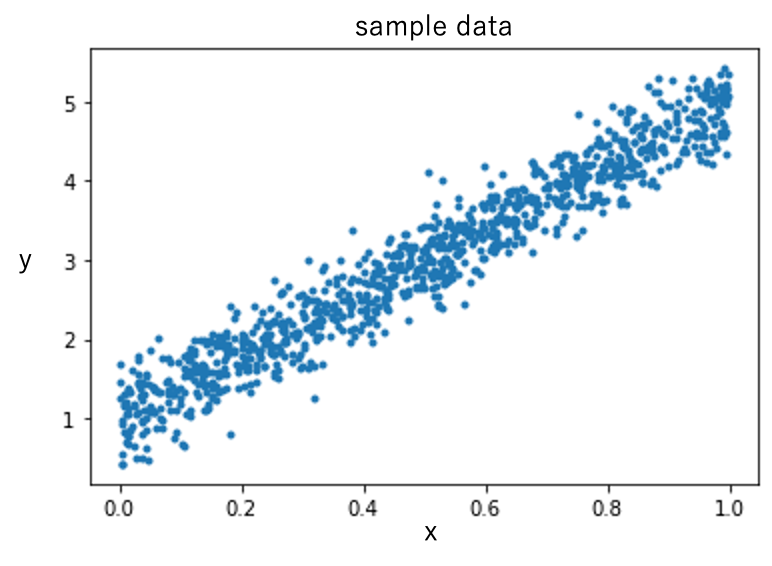
• このデータに対して、ベイズ線形回帰を行なっていきます

変分推論

• はじめにモデルの定義を行います
• 今回のモデルではパラメータが二つ（w_0とw_1）なので、それぞれ設定します
• このモデルでは線形結合モデルの出力y_にノイズを加えた出力をyとしてサンプリングします
• ここで変数y_はモデル出力、yはモデル出力にノイズが乗ったデータとして区別しておきます

モデル定義

# モデル定義
def model(x, y):
    # パラメータの事前分布
    w0 = pyro.sample("w0", dist.Normal(0, 10))
    w1 = pyro.sample("w1", dist.Normal(0, 10))
    # 尤度（obsに観測値を渡す）
    with pyro.plate("plate", x.shape[0]):
        y_ = w0 + w1 * x
        y = pyro.sample("y", dist.Normal(y_, 1), obs=y)
    return y_

ガイド定義（手動）

• つぎに変分推論用のガイドを定義します
• ガイドの設定は手動で設定する方法とpyroに自動で設定してもらう方法があります
• 手動設定の場合は、パラメータ(w_0, w_1)のサンプリングをゴールとして、そこに必要な変分パラメータを設定します
• 今回はパラメータ(w_0, w_1)は正規分布に従うと仮定したので、正規分布に必要なパラメータである平均（mu）と標準偏差（sigma）をそれぞれ設定します

# ガイド（変分推論で用いる近似事後分布の設定）
def guide(x, y):
    # 変分パラメータ（分布の仮定や制約条件を追加できる）
    w0_mu = pyro.param("w0_mu", torch.tensor(0.0))
    w0_sigma = pyro.param("w0_sigma", torch.tensor(1.0), constraints.positive)
    w1_mu = pyro.param("w1_mu", torch.tensor(0.0))
    w1_sigma = pyro.param("w1_sigma", torch.tensor(1.0), constraints.positive)
    # サンプリング
    pyro.sample("w0", dist.Normal(w0_mu, w0_sigma))
    pyro.sample("w1", dist.Normal(w1_mu, w1_sigma))

ガイド定義（自動）

• pyroに自動で近似事後分布を設定してもらう方法です
• 定義したモデルを渡すだけで、自動でガイド関数を取得することができるので非常に強力です
• ただし、この方法は各パラメータに対して独立の多次元正規分布を仮定しています
• より細かい前提情報を反映したい場合は手動設定をする必要があります

# ガイド（変分推論で用いる近似事後分布の設定）
guide = infer.autoguide.guides.AutoDiagonalNormal(model)

補足：AutoDiagonalNormalについて

• AutoDiagonalNormalによる変分近似分布は分散共分散行列が対角行列となる多次元正規分布を仮定している

• 今回の場合、パラメータ w_0 と w_1 に対して $\mathbf w = (w _ 0, w _ 1) ^ {\mathbf T}$ を二次元の確率変数ベクトルとして、多次元正規分布を以下の様に表現する
  $$q(w _ 0, w _ 1) = {\rm Normal} (\mathbf m , \mathbf \Sigma)$$
  ここで、
  $$\mathbf m = (m _ {w _ 0}, m _ {w _ 1} ) ^ {\mathbf T}$、$\mathbf \Sigma = {\rm diag} (\sigma _ {w _ 0}, \sigma _ {w _ 1})$$

• 分散共分散行列が対角成分にしか値を持たないということは、各成分が互いに無相関だということを仮定している

• w_0, w_1には相関があると仮定する場合は、対角でない分散共分散行列を持つ正規分布を仮定する必要がある

推論

• 定義したモデルとガイドを利用して変分推論を行います
• 推論方法はpytorchと非常に似ており、torchユーザーであれば違和感なく使えると思います

# パラメータの初期化
pyro.clear_param_store()
# 最適化関数
oprimizer = pyro.optim.Adam({"lr": 1e-1, "betas": (0.95, 0.999)})
# 損失関数（変分下界ELBOを指定）
loss = infer.Trace_ELBO()
# 確率的変分推論（Stochastic Variational Inference）
svi = infer.SVI(model, guide, oprimizer, loss)

# 推論実行
n_steps = 5000
loss = []
for i in range(n_steps):
    elbo = svi.step(x, y)
    if i % 1000 == 0:
        print("Elbo loss: {}".format(elbo))
    loss.append(elbo)

予測（事後分布サンプリング）

• 推論が完了したので、最後に予測（事後分布サンプリング）を行います
• パラメータ（回帰係数）の事後分布とモデルの予測値の事後分布を取得します
• pyroではinfer.Predictive関数が用意されており、ここに学習済みのモデルを入力するとサンプリング結果が得られます
• 返り値を確認すると分かるのですが、一つの予測値に対して、指定したサンプル数分のデータが戻るので、各予測値に対する出力はスカラーでなくベクトルである点に注意が必要です
• ここでは出力結果の平均値や5~95%区間を得るためのサマリ関数を用いて、サンプリング結果を集約しています

# 予測モデルの構築
pred_model = infer.Predictive(model=model, guide=guide,num_samples=2000, return_sites=["w0", "w1", "y", "_RETURN"])

# 事後分布の予測値（サンプリング結果）の取得
pred_sample = pred_model(x, None)

# 予測値はdict形式
print(pred_sample.keys())

• まず、パラメータの事後分布を可視化します
• pred_sampleにdict型で2000件分のサンプリング結果が格納されています

fig, ax = plt.subplots(ncols=2, figsize=(10, 5))

ax[0].hist(pred_sample['w0'].reshape(-1).detach().numpy(), bins=20, alpha=.7)
ax[0].set_title("SVI) Params: w0")

ax[1].hist(pred_sample['w1'].reshape(-1).detach().numpy(), bins=20, alpha=.7)
ax[1].set_title("SVI) Params: w1")

• 真値がw_0=1.0, w_1=4.0なのでそれなりに良い推定結果が得られています
• また、分布も正規分布型なので、それぞれの平均値を代表値とする回帰係数を用いて問題なさそうです

予測値・ベイズ信用区間

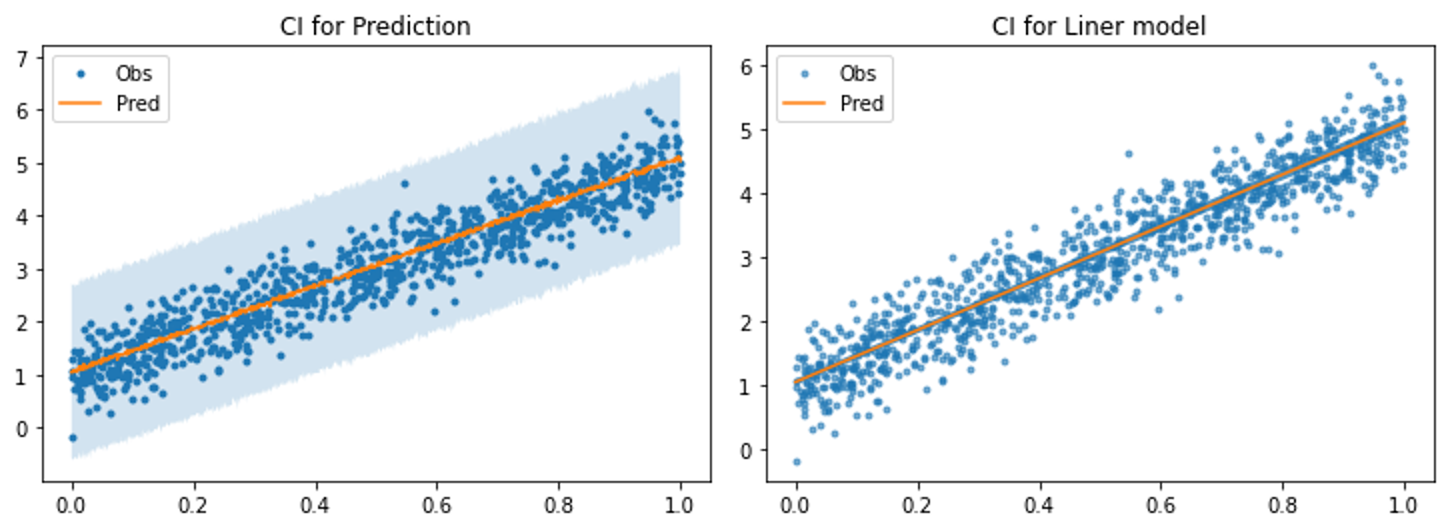
• 最後に事後分布のサンプリング結果を可視化してみます
• モデルそのもの予測結果とノイズが乗った予測結果の2つを出力してみます
• 両者を明示的に分離して評価できる点もベイズモデリングの便利な点かと思います

# サンプリング結果のサマリー関数
def summary(samples):
    site_stats = {}
    for k, v in samples.items():
        site_stats[k] = {
            "mean": torch.mean(v, 0),
            "std": torch.std(v, 0),
            "5%": v.kthvalue(int(len(v) * 0.05), dim=0)[0],
            "95%": v.kthvalue(int(len(v) * 0.95), dim=0)[0],
        }
    return site_stats

pred_summary = summary(pred_sample)

# 予測値の事後分布の平均と標準偏差の取得
pred_df = pd.DataFrame({
    # 観測値
    "x": x.detach().numpy(),
    "y": y.detach().numpy(),
    # サンプリング結果（モデルアプトプット＋ノイズ）
    "y_mean": pred_summary['y']['mean'].detach().numpy(),
    "y_lower": pred_summary['y']['5%'].detach().numpy(),
    "y_upper": pred_summary['y']['95%'].detach().numpy(),
    # モデルの出力
    "return_mean": pred_summary['_RETURN']['mean'].detach().numpy(),
    "return_lower": pred_summary['_RETURN']['5%'].detach().numpy(),
    "return_upper": pred_summary['_RETURN']['95%'].detach().numpy()
})

pred_df.sort_values(by=['x'], inplace=True)

# サンプリング結果（モデルアプトプット＋ノイズ）----------
plt.plot(pred_df["x"], pred_df["y"], ".", label='Obs')
plt.plot(pred_df["x"], pred_df["y_mean"], "-", label='Pred')

# ベイズ信用区間（95%）
plt.fill_between(pred_df["x"],
                 pred_df["y_lower"], 
                 pred_df["y_upper"], 
                 alpha=0.2)

plt.title("CI for Prediction")
plt.legend()

# サンプリング結果（モデルの出力）----------
plt.plot(pred_df["x"], pred_df["y"], ".", label='Obs', alpha=.6)
plt.plot(pred_df["x"], pred_df["return_mean"], "-", label='Pred')

# ベイズ信用区間（95%）
plt.fill_between(pred_df["x"],
                 pred_df["return_lower"], 
                 pred_df["return_upper"], 
                 alpha=0.8)

plt.title("CI for Liner model")
plt.legend()

さいごに

本記事では、pyroを利用したベイズ線形回帰の実装例を示しました。
まだpyroによるベイジアンモデルの解説資料は多くは出回っておらず、資料ごとにモデルやガイドの書き方が様々なので混乱の原因になったりします。
そこで本記事では、今後の様々な実装の見通しが立ちやすくなるように代表的な手順を整理してみました。
今回は最もベーシックな線形回帰ですが、モデル内のリンク関数を変更すれば一般化線形回帰に拡張したり、pyroはガウス過程や状態空間モデル、ベイズ深層学習にも対応できるみたいなので、今後時間があれば試してみようと思います。