基本的な線形回帰の基本的な説明と実装

はじめに

• 統計・機械学習の基本中の基本である線形回帰を簡易的な数式＆スクラッチで実装してみました
• 理解の為の実装なので、パフォーマンスはパッケージを利用したほうが最適化されています
• 回帰分析の基本を正しく理解しておけば、その先の一般化線形モデルや機械学習の理解にも繋がるかと思います

線形回帰とは

• 一言でいうと、「データに対して、最もよく当てはまる線を引くこと」
• イメージ：データ（青点）に対して、最もよく当てはまる線（赤線）を引く
  

"最もよく当てはまる"とは？

• 「最小二乗法」という手法で近似を算出する
• 最小二乗法では、予測値と実測値の誤差が最小になるようパラメーターを推定する
• 符号のプラスマイナスを考慮して、誤差は二乗して合計値を考える
• C（最小化したい関数） = {y(実測値)　- y_(予測値)}**2の合計値

計算アルゴリズムの解説・実装

• 早速、中身を見ていく （今回は以下の３つを説明）
  1. 原点を通る直線でモデル化（y = ax）
  2. 直線でモデル化（y = ax + b）
  3. 多変数でモデル化（y = Xw） *いわゆる重回帰分析

原点を通る直線でモデル化（y = ax）

計算アルゴリズム

• x, y を以下のように表現します

\begin{aligned}
x=\left( x_{1},\ldots ,x_{n}\right) ^{T}, y=\left( y_{1},\ldots ,y_{n}\right) ^{T}\\
\end{aligned}

• 予測値を下記のモデルで表します

\begin{aligned}
\widehat {y}=ax\\ 
\end{aligned}

• 最小化したい関数Cを定義します

\begin{aligned}
c=\sum ^{n}_{1}
\left( y-\widehat {y}\right) ^{2}
\end{aligned}

• 変数aで関数Cを微分し、"=0"となる変数aを求める

\begin{aligned}\dfrac {\partial C}{\partial a}=\sum ^{n}_{1}\left( y-\widehat {y}\right) ^{2}\\ =\sum ^{n}_{i}\left( 2x^{2}a-2xy\right) =0\\ \therefore a=\dfrac {\sum ^{n}_{i}x\cdot y}{\sum ^{n}_{i}x^{2}}=\dfrac {x^{T}y}{\left\| x\right\| ^{2}}\end{aligned}

• 実装では、以下の部分の関数を定義して、パラメータを算出します

\begin{aligned}\
a=\dfrac {\sum ^{n}_{i}x\cdot y}{\sum ^{n}_{i}x^{2}}=\dfrac {x^{T}y}{\left\| x\right\| ^{2}}
\end{aligned}

実装

• 関数の定義

def lr_1(x, y):
    a = np.dot(x, y)/(x**2).sum()
    return a

• サンプルデータにフィット（パラメータの計算）
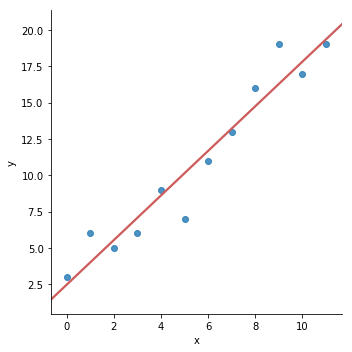
• 結果をグラフで可視化

a = lr_1(x, y)
y_ = a*x

plt.figure(figsize=(5, 5))
plt.scatter(x, y)
plt.plot(x, y_, c='indianred')

直線でモデル化（y = ax + b）

計算アルゴリズム

• 予測値を下記のモデルで表します

\begin{aligned}
\widehat {y}=ax+b\\ 
\end{aligned}

• 最小化したい関数Cを定義します

\begin{aligned}
C=\sum ^{n}_{1}\left( y-\widehat {y}\right) ^{2}\\ 
\dfrac {\partial C}{\partial a}=0,\dfrac {\partial C}{\partial b}=0\\
\end{aligned}

• 関数Cを変数a、bでそれぞれ微分し、"=0"となる変数a, bを求めます

\begin{aligned}
a=\dfrac {\sum ^{n}_{1}xy-\dfrac {1}{n}\sum ^{n}_{1}x\sum ^{n}_{1}y}{\sum ^{n}_{1}x^{2}-\dfrac {1}{n}\left( \sum ^{n}_{1}x\right) ^{2}}\\ b=\dfrac {1}{n}\sum ^{n}_{1}\left( y-ax\right)
\end{aligned}

• 実装では、以下の部分の関数を定義して、パラメータを算出します

\begin{aligned}
a=\dfrac {\sum ^{n}_{1}xy-\dfrac {1}{n}\sum ^{n}_{1}x\sum ^{n}_{1}y}{\sum ^{n}_{1}x^{2}-\dfrac {1}{n}\left( \sum ^{n}_{1}x\right) ^{2}}\\ b=\dfrac {1}{n}\sum ^{n}_{1}\left( y-ax\right)
\end{aligned}

実装

• 関数の定義

def lr_2(x, y):
    a_nume = np.dot(x, y) - x.sum() * y.sum() / len(x)
    a_denom = (x**2).sum() - x.sum()**2/len(x)
    a = a_nume/a_denom
    b = (y.sum() - a * x.sum() )/ len(x)
    return a, b

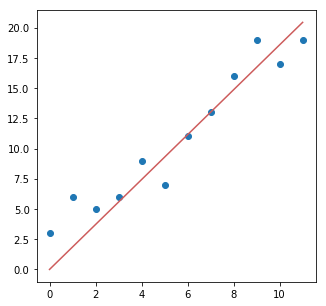
• サンプルデータにフィット（パラメータの計算）
• 結果をグラフで可視化

a, b = lr_2(x, y)
y_ = a*x + b

plt.figure(figsize=(5, 5))
plt.scatter(x, y)
plt.plot(x, y_, c='indianred')

多変数でモデル化 （y = Xw）

計算アルゴリズム

※ ここでは正規方程式（Normal Equation）という方法で直接的にパラメータを計算する方法を採用します　（計算方法は他にも勾配降下法や最尤推定法があります）

• 求めたいパラメータのベクトルをwと表現します

\begin{aligned}
\omega =\left( \omega _{0},\omega _{1},\ldots ,\omega _{n}\right) \\ 
\end{aligned}

• 予測値を下記のモデルで表します

\begin{aligned}
\widehat {y}=X\omega \\ 
\end{aligned}

• 最小化したい関数Cを定義します

\begin{aligned}
C=\left\| y-\widehat {y}\right\| ^{2}\\ =\left( y-X\omega \right) ^{T}\left( y-X\omega \right) \\ 
=y^{T}y-\omega ^{T}X^{T}y-y^{T}X\omega +w^{\tau }X^{T}Xw
\end{aligned}

• 勾配ベクトルを求めます

\begin{aligned}
\nabla C\left( \omega \right) =-2Xy+2X^{T}X\omega =0\\ X^{T}X\omega =Xy\\ 
\left( X^{T}X\right) ^{-1}\left( X^{T}X\right) \omega =\left( X^{T}X\right) ^{-1}Xy\\ \omega =\left( X^{T}X\right) ^{-1}Xy\end{aligned}

• 実装では、以下の部分の関数を定義して、パラメータを算出します

\begin{aligned}
\omega =\left( X^{T}X\right) ^{-1}Xy\end{aligned}

実装

• 関数の定義

def lr_3(X, y):
    one = np.ones(X.shape[0]).reshape(-1, 1)
    X_ = np.concatenate((one, X), axis=1)
    A = np.dot(X_.T, X_)
    B = np.dot(X_.T, y)
    w = np.dot(np.linalg.inv(A), B)
    return w

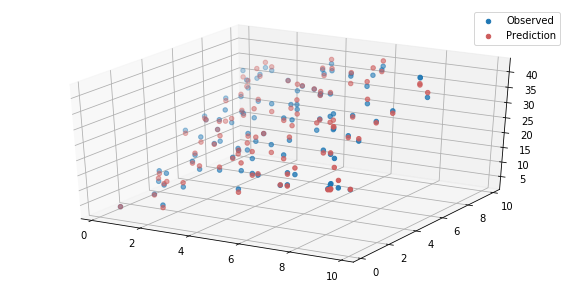
• 多次元のデータを新規作成
• サンプルデータにフィット（パラメータの計算）
• 結果をグラフで可視化（3次元プロット）

# サンプルデータの作成
n = 100
X = np.random.random((n, 2))*10
w0, w1, w2 = 1, 2, 3
y = w0 + w1 * X[:,0] + w2 * X[:,1] + np.random.randn(n)

# パラメータ推定
w0_, w1_, w2_ = lr_3(X, y)
y_ = w0_ + w1_ * X[:,0] + w2_ * X[:,1]

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:,0], X[:,1], y, label='Observed')
ax.scatter(X[:,0], X[:,1], y_, color = 'indianred', label='Prediction')
plt.legend()

<おまけ>　汎化性能を高めるための方法（リッジ回帰）

• 通常の線形回帰は外れ値・異常値に弱いので、正則化項を追加することで汎化性能の向上が期待できます
• ここでは、リッジ回帰を解説します（汎化性能を高めるための方法は多々あります）

計算アルゴリズム

• 最小化したい関数Cに正則化項を追加します
• これにより、Cを最小化しつつ、wの大きさも最小化するモチベーションが働きます（lambdaはハイパーパラメータで任意に決める）

\begin{aligned}C\left( \omega \right) =\left\| Y-X\omega \right\| ^{2}+\lambda \left\| w\right\| ^{2}\\ 
\end{aligned}

• 同様に勾配ベクトルを求めます

\begin{aligned}
\nabla C=2X^{T}X\omega -2X^{T}y+2\lambda \omega =0\\ \omega =\left( X^{T}X+\lambda I\right) ^{-1}X^{T}y\end{aligned}

• 実装では、以下の部分の関数を定義して、パラメータを算出します

\begin{aligned}
\omega =\left( X^{T}X+\lambda I\right) ^{-1}X^{T}y\end{aligned}

実装

• 関数の定義

def lr_ridge(X, y, lam):
    one = np.ones(X.shape[0]).reshape(-1, 1)
    X_ = np.concatenate((one, X), axis=1)
    c = np.eye(X_.shape[1])
    A = np.dot(X_.T, X_) + lam * c
    B = np.dot(X_.T, y)
    w = np.dot(np.linalg.inv(A), B)
    return w

• サンプルデータにフィット（パラメータの計算）
• 結果をグラフで可視化（3次元プロット）

# パラメータ推定
w0_, w1_, w2_ = lr_ridge(X, y, lam=1.0)
y_ = w0_ + w1_ * X[:,0] + w2_ * X[:,1]

fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:,0], X[:,1], y, label='Observed')
ax.scatter(X[:,0], X[:,1], y_, color = 'indianred', label='Prediction')
plt.legend()

• 今回のサンプルデータだと、通常の線形回帰もリッジ回帰も差が見られませんでした
• 汎化性能を比較した良い記事が他にたくさんあるので、モデルの頑健性について興味のある方はそちらの比較を参照ください
• 参考：
• OLS、リッジ回帰、ラッソでのパフォーマンス比較
• 【機械学習】ラッソ回帰・リッジ回帰について　メモ

さいごに

• 日頃から便利なパッケージを使っていると簡単に計算結果が出てしまうのですが、分析手法の選択や結果の正しい解釈に基本的な理解は必要だと思います
• 自分の理解の為にも改めて、線形回帰の基本事項を整理してみました
• NOTE: 数学や統計的な厳密さより、分かりやすさを優先に書いていますが、誤記等あればご指摘ください