機械学習で使用することを前提に、ラッソ回帰およびリッジ回帰についてまとめていきます。数式は省きます(わからないので)。概念だけ。
ど文系が書いていますので、何か誤りなどがあれば指摘していただけると嬉しいです。
ラッソ回帰とは
直線回帰に正則化項の概念を加えた回帰分析。
最小二乗法の式に正則化項(L1ノルム)を加え、その最小を求めることでモデル関数を発見する。
リッジ回帰とは
直線回帰に正則化項の概念を加えた回帰分析。
最小二乗法の式に正則化項(L2ノルム)を加え、その最小を求めることでモデル関数を発見する。
ラッソ回帰とリッジ回帰の違い
最小二乗法に正則化項を加えたもの、という点ではラッソとリッジは同じもの。
ただし、どのような値を正則化項とするかという点で2つは異なる。
正則化項の違いにより生まれる差異は次の通り。
| 名称 | 正則化項 | 特徴 |
|---|---|---|
| ラッソ回帰 | L1ノルム | 不要なパラメータ(次元・特徴量)を削ることができる |
| リッジ回帰 | L2ノルム | 過学習を抑えることができる |
| 直線回帰 | なし | 過学習を起こしやすい |
プログラムによる可視化
ラッソ回帰におけるパラメータの削減とはどういうことなのか、などをプログラムを通して可視化する。
import pandas as pd
import matplotlib.pyplot as pyp
import numpy as np
from numpy.random import *
from sklearn.linear_model import LinearRegression,Ridge,Lasso
from sklearn.datasets import load_boston
# サンプルデータを用意
dataset = load_boston()
# 標本データを取得
data_x = pd.DataFrame(dataset.data,columns=dataset.feature_names)
# 正解データを取得
data_y = pd.DataFrame(dataset.target,columns=['target'])
# サイズが大きいので、データ数を圧縮
size = len(data_x.index) - 10
for i in range(size):
data_x = data_x.drop(i)
data_y = data_y.drop(i)
data_y = data_y.as_matrix().ravel()
# 回帰直線、ロッソ、リッジのモデルを生成
lr = LinearRegression()
lasso = Lasso()
ridge = Ridge()
# モデル関数を作成
lr.fit(data_x, data_y)
lasso.fit(data_x, data_y)
ridge.fit(data_x, data_y)
# 直線回帰、ラッソ回帰、リッジ回帰で算出されたモデル関数を図示
pyp.plot(lr.predict(data_x), linestyle="solid",
color="black",label="lr")
pyp.plot(lasso.predict(data_x), linestyle="solid",
color="red", label="lasso")
pyp.plot(ridge.predict(data_x), linestyle="solid",
color="blue", label='ridge')
pyp.title("lr,Lasso,Ridge")
pyp.legend(loc="lower right")
pyp.show()
print('lassoとridgeの回帰係数')
reg_coef=[]
reg_coef.append([lasso.coef_])
reg_coef.append([ridge.coef_])
print(reg_coef)
# 出力結果
lassoとridgeの回帰係数
[[array([ 0. , 0. , 0. , 0. , -0. ,
0. , 0. , -0. , -0. , -0.00883661,
0. , -0.26515107, -0. ])], [array([ 2.53025857e-01, 0.00000000e+00, -1.37577146e-05,
0.00000000e+00, 7.37020424e-08, 3.28166354e+00,
-2.43832964e-02, -1.18846289e+00, 3.07091843e-05,
7.24736750e-04, -1.10553064e-05, -4.45850693e-01,
1.99762992e-01])]]
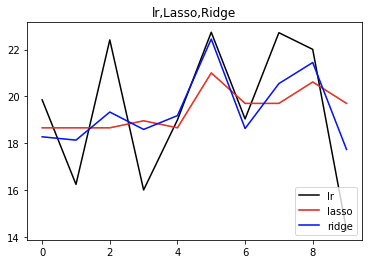
直線回帰、ラッソ回帰、リッジ回帰で求められたモデル関数を図示したものが上の図。黒が直線回帰、赤がラッソ、青がリッジ。
ラッソとリッジのグラフを比べた時、ラッソの方がブレが小さいことが見て取れる。
これは、ラッソがパラメータの圧縮を行なっていることに起因する。
ラッソとリッジの回帰係数を改めて見てみる。
lassoとridgeの回帰係数
[[array([ 0. , 0. , 0. , 0. , -0. ,
0. , 0. , -0. , -0. , -0.00883661,
0. , -0.26515107, -0. ])], [array([ 2.53025857e-01, 0.00000000e+00, -1.37577146e-05,
0.00000000e+00, 7.37020424e-08, 3.28166354e+00,
-2.43832964e-02, -1.18846289e+00, 3.07091843e-05,
7.24736750e-04, -1.10553064e-05, -4.45850693e-01,
1.99762992e-01])]]
ラッソ側は、ほとんどの特徴量を0として処理したのに対して、リッジ側では全ての特徴を切り捨てることなく処理している。
これがグラフの差分に繋がっており、そのままラッソとリッジの違いとなる。
ラッソ回帰ではパラメータの圧縮=判断に用いる特徴量の選択を行い、リッジ回帰ではそれを行わない。
どの特徴量がグラフに影響を与えているのかを見つけるにはラッソを用いるのがベターであり、(単純な最小二乗法よりも)過学習を抑えつつ相関を見つけたいならばリッジがベターである。
以上。