LTspice で PLL 回路を解析する
Spice って、結局、(AC解析の場合は) 伝達関数を行列計算で解いてるだけなので、解く対象が電圧・電流じゃなくても構わないんです。
例えば、PLL (Phase Lock Loop) 回路は、電圧・電流じゃなく、周波数やら位相やらをループ制御する回路ですが、こういうものでも LTspice で解析できます。
ここでは、計算に使用する部品の定義から解説して、最終的には、PLL回路 (最近主流のデジタルPLL) の、
- オープンループ特性
- 位相雑音特性
- Lock up time
について解析してみます。
部品定義
VCO
電圧制御電圧源で表します。
VCO の制御電圧は、そのまま電圧制御電圧源の入力電圧ですが、出力されるのは電圧ではなく、周波数だと考えます。
もちろん LTspice 上は、電圧として、単位 V なんかで表示されるでしょうが、Hz なんだ、という目で見てください。
VCO の 変調感度が Kv[Hz/V]、制御電圧=0 での発振周波数が f0[Hz] ならば、出力周波数は f = f0 + Kv・V ですから、f0 の固定電圧源と、係数 Kv の電圧制御電圧源で VCO のモデルになります。
さらに、位相ノイズとして、ノイズ電圧源(サーマルノイズ、フリッカーノイズ)を加えます。
(ノイズ電圧源については 別記事 を参照してください。)
回路図とシンボルは以下のようになります。

パラメータとして(Attributes の 、Value〜SpiceLine2 までフルに使って記述してます)、f0 は 制御電圧=0 での発振周波数[Hz]、Kv は 変調感度[Hz/V]、PhaseNoise1k は 1kHz offset における SSB Phase Noise [dBc/Hz]、PhaseNoise1M は 1MHz offset における SSB Phase Noise [dBc/Hz]、PhaseNoiseFloor は、さらに offset 周波数が高いところにおいて、SSB Phase Noise がフロア(一定値)になるところでの値 [dBc/Hz] を表しています。位相雑音はサーマルノイズ起因の場合は offset 周波数に対して -20dB/dec の傾きになりますが、offset 周波数の小さいところではフリッカーの影響をうけて -30dB/dec の傾きとなり、offset 周波数が高いところでは出力のサーマルノイズに達して一定値となります。これらを表現するために、位相雑音に関しては3つのパラメータを用いており、それぞれ値を設定することで、それっぽい結果が得られるように式を定義してあります。
雑音に関する部品は、AC 解析や Transient 解析では何の影響も与えません。Noise 解析のときのみ、その影響が現れます。では、この VCO のノイズがどうなっているか、解析してみようと思うのですが、その前に、ここで解析したいのは、位相雑音であって、周波数雑音(?)ではない、ということに注意してください。
この VCO モデルの出力は、周波数になっているので、位相雑音として評価するには、出力値を位相に変換してやる必要があるのです。というわけで、周波数を位相に変換するブロックの回路図とシンボルです。
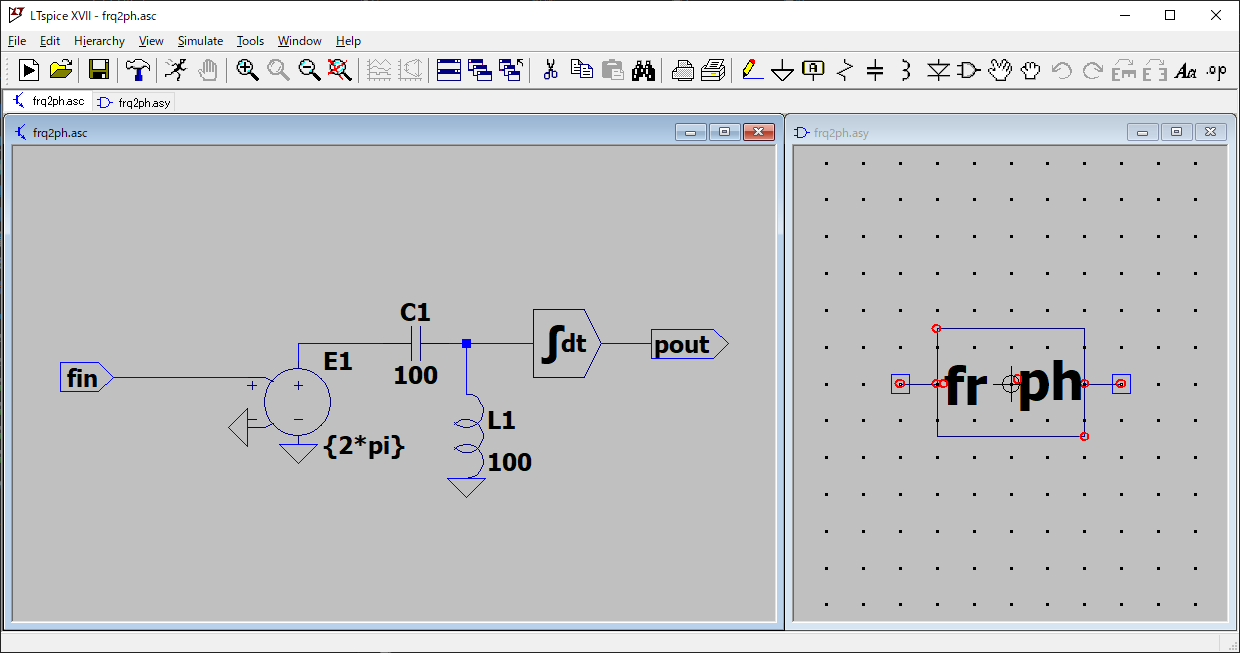
位相は角周波数を積分したものなので、2πかけて積分すればよいのです。
( 信号の時間微分・積分については 別記事 を参照してください。)
ただし、DC(つまり発振周波数そのもの) 成分は積分すると発散(→∞)するので、積分の前にカットしています (AC 成分だけ確認できればよい)。
これを用いて、VCO のノイズ解析をやってみます。以下のようなベンチを動かして、位相雑音計算結果をプロットします。

プロットするのは、pmon のノイズを 1/√2 かけて、20log とったものです。1/√2 倍してるのは、ここで計算されるノイズは、発振周波数の上と下のスペクトラム両方を含むからで、通常は SSB (Single Side Band) で片側だけを評価するので、半分のパワーにしてる、って意味です。
どうでしょうか? 100kHz 〜 1MHz あたりは -20dB/dec の傾き、10kHz 以下あたりは -30dB/dec の傾きになって、パラメータで与えた通りの雑音値になってるように見えるでしょうか?
VCO のモデルはこんな感じです。実際の設計では、データシートから各パラメータは読み取れると思います。
Reference XTAL
リファレンスとなるクリスタル発振器です。これも VCO と同様ですが、与えるパラメータは発振周波数 f0[Hz]、1kHz offset における SSB Phase Noise [dBc/Hz]、フロアのノイズ [dBc/Hz] です。

これも単体での位相雑音を解析してみると、以下のようになります。

周波数分周器と逓倍器
PLL では VCO の発振周波数と XTAL の発振周波数をそれぞれ適当に分周して同じ周波数とし、その比較を行います。そこで、周波数分周器が必要になります。後の例では使用していませんが、より高い発振周波数を得るために、周波数逓倍器により発振周波数を整数倍にすることもあります。
回路図上は電圧だけど、本当は周波数を表しているんだと考えると、周波数分周器・逓倍器は以下のようになります。


最近の PLL では分数分周ができるものも多いので、その場合の分周器の N は整数でなくてOKです。
位相比較器+チャージポンプ出力
入力の VCO, XTAL の信号を周波数分周し、位相比較して、チャージポンプ電流出力する、いわば PLL のキモの部分のブロックです。回路図とシンボルは以下のようになります。

入力の周波数は、先に示した周波数分周器で同じ周波数になるよう、分周されます。fin_n が VCO からの入力で、fin_p が XTAL からの入力です。それらを比較するのですが、PLLでは比較するのは周波数ではなく位相なので、差をとった後、2π倍して時間積分し、位相の差とします。そこにノイズを加え、電流として出力します。 R1 は特に無くても大丈夫かもしれないですけど、収束が悪かったらこの辺の値で調整したりします。
パラメータ多いですが、順に説明していきます。
Icp[A] = チャージポンプ電流出力ですが、これは PLL IC では内部レジスタ等で設定可能となっているものが多いので、実際の設計では自分が設定した値を渡します。チャージポンプでは、位相差に応じてパルスの電流を吐き出し、もしくは引き込みで出力します。位相差とパルスの Duty が比例しており、位相差 2πで Duty 100% の計算です。Plarity は位相比較の極性で、+1 もしくは -1 を与えます。
Counter N は VCO 側の信号入力に入る周波数分周器の分周数で、Counter R は XTAL 側の分周数であり、これらも通常内部レジスタで設定可能です。 (VCO 発振周波数)/N と (XTAL 発振周波数)/R を同じにする必要があり、その周波数が位相比較周波数 = RefFreq[Hz] になります。
最後に Normalized Phase Noise Floor [dBc/Hz] ですが、これは PLL IC 内部のノイズを表すもので、データシート上にその名の通り(もしくはそれに近い名前)の値で載っているはずです。
解析例
それではここまでで揃えた部品を並べて、あとはループフィルタを設計すれば、PLL 回路の完成です。
基本的に、どれも同じ回路図で解析していますが、解析の種類に応じて、spice directive とか、若干違うところがあります。
オープンループ特性
AC 解析で、ループの安定性を確認する計算です。
(ループ回路でオープンループ特性を見る方法については 別記事 を参照してください。)


V(vo)/V(vi) をプロットして、ゲイン=0 となるところでの位相、位相余裕を確認します。ここでは 70°程度とれてるので、十分です。
位相雑音特性
NOISE 解析を行い、結果を位相雑音として見るために、VCO 出力に 周波数→位相変換を入れてそこでのノイズを確認しています。
また、.meas 文で 100kHz から 100MHz のノイズの積分値およびそのdB換算値を計算しています。結果は View→Spice Error Log で見ることができます。


オープンループ特性から、fL = 30kHz ぐらいであることがわかっているので、30kHz あたりから下の offset 周波数では、位相雑音の圧縮がかかっているはずです。それより上の周波数では、もとの VCO の Phase Noise に近い値になります。逆に offset 周波数の低い範囲では XTAL の位相雑音で決定される値になります。
Lock up time
Transient 解析で、周波数の引き込み時間を調べています。100 〜 150 usec ぐらいで周波数の引き込みが終わる様子がわかります。

