TensorFlowのOptimizerの違いによる学習推移の比較

最適化問題をTensorFlowのOptimizerを使って求め、収束の仕方のOptimizerによる違いを見ます。

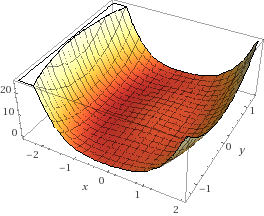
この記事で解く最適化問題は2変数で $ (x^2 + y^2 - 1)^2 + x $ が最小値となる $ x $、$ y $ です。

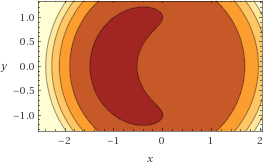
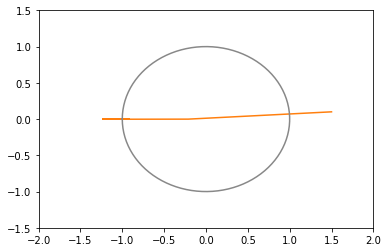
この関数はxyの座標でいうと、原点を中心に半径1の円から少し左にずれた円周状に谷になっていて、その中でも左のほうが低くなっております。

ディープラーニングとはパラメータの数がぜんぜん違いますので、挙動もまたぜんぜん違うのだとは思いますが、Optimizerによる動き方の違いをイメージできるかもしれません。

Pythonのコードはこんな感じです。Google Colaboratoryで実行しました。

import time
import numpy as np
import matplotlib.pyplot as plt
import math
import tensorflow as tf

opt1 = tf.optimizers.SGD(learning_rate=0.3) # 青
opt2 = tf.optimizers.SGD(learning_rate=0.2) # 橙
opt3 = tf.optimizers.SGD(learning_rate=0.1) # 緑
opt4 = tf.optimizers.SGD(learning_rate=0.05) # 赤 

opts = [opt1, opt2, opt3, opt4]

# 目的となる損失関数
def loss(i):
  x2 = x[i] * x[i]
  y2 = y[i] * y[i]
  r2 = (x2 + y2 - 1.0)
  return r2 * r2 + x[i]

# 最適化する変数
x = []
y = []

# グラフにするための配列
xHistory = []
yHistory = []
lossHistory = []
calculationTime = []
convergenceCounter = []

maxLoopCount1 = 100
maxLoopCount2 = 1000

for i in range(len(opts)):
  # 適当な初期値
  x.append(tf.Variable(1.5))
  y.append(tf.Variable(0.1))

  # グラフにするための配列
  xHistory.append([])
  yHistory.append([])
  lossHistory.append([])
  convergenceCounter.append(0)

  start = time.time()

  for loopCount in range(maxLoopCount2):
    l = float(loss(i))
    # グラフにするために記録
    if loopCount < maxLoopCount1:
      xHistory[i].append(float(x[i]))
      yHistory[i].append(float(y[i]))
      lossHistory[i].append(l)
    if (l >= -1.056172): # 収束の閾値
      # 収束までの回数を測定するため
      convergenceCounter[i] = loopCount + 1

    # 最適化
    opts[i].minimize(lambda: loss(i), var_list = [x[i], y[i]])

  calculationTime.append(time.time() - start)

colors = ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728', '#9467bd', '#8c564b', '#e377c2', '#7f7f7f', '#bcbd22', '#17becf']

# グラフ化1つ目: 損失関数の値の推移
plt.ylim(-1.1, +3.5)
for i in range(len(opts)):
  plt.plot(range(maxLoopCount1), lossHistory[i], color=colors[i % len(colors)])
plt.show()

# グラフ化2つ目以降: xy平面上での推移
for i in range(len(opts)):
  print("time: " + str(calculationTime[i]))
  print("convergenceCounter: " + str(convergenceCounter[i]))
  print("loss: " + str(lossHistory[i][-1]))
  plt.xlim(-2, +2)
  plt.ylim(-1.5, +1.5)
  plt.plot(xHistory[i], yHistory[i], color=colors[i % len(colors)])
  th = np.linspace(-math.pi, math.pi, 100)
  plt.plot(np.cos(th), np.sin(th), color="#888888")
  plt.show()

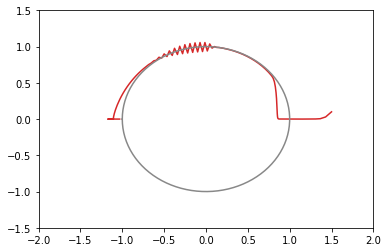
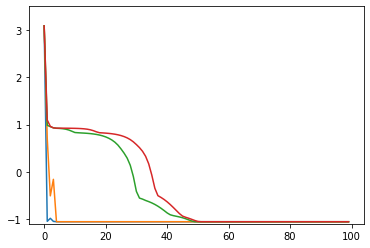
シンプルな勾配降下法

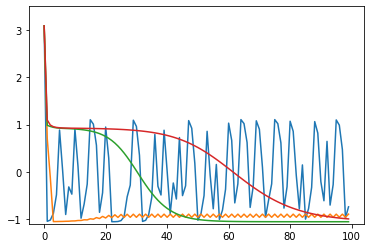
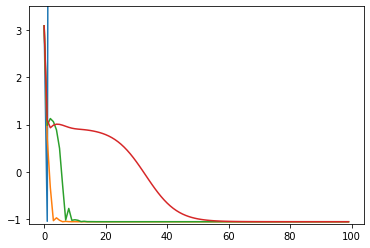
opt1 = tf.optimizers.SGD(learning_rate=0.3) # 青: ぜんぜん収束しない
opt2 = tf.optimizers.SGD(learning_rate=0.2) # 橙: おしいけど細かい振動が続く
opt3 = tf.optimizers.SGD(learning_rate=0.1) # 緑: 108回で収束
opt4 = tf.optimizers.SGD(learning_rate=0.05) # 赤: 収束しそうだけど1000回でも到達せず
# ちなみに learning_rate=0.4 では発散する

• 学習率を適切に設定しないと収束しない

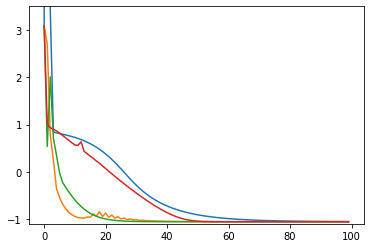
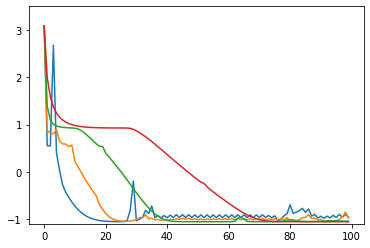
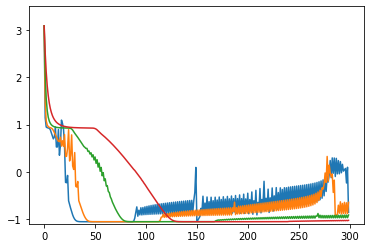
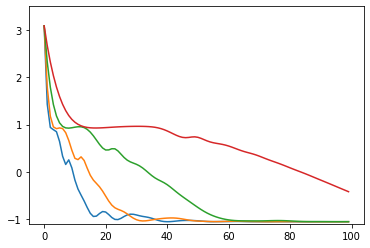
損失関数の値の推移のグラフ（100回まで）

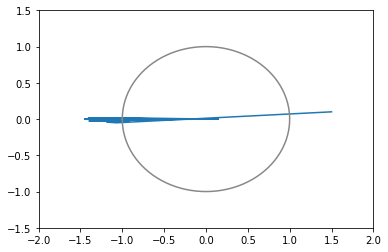
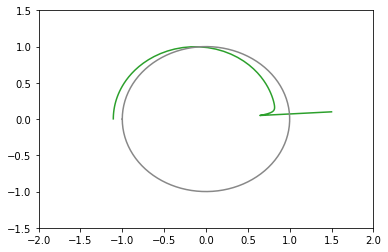
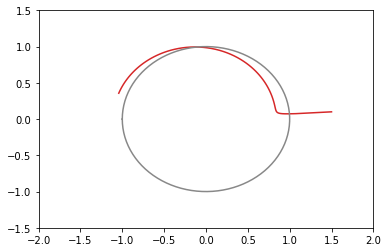
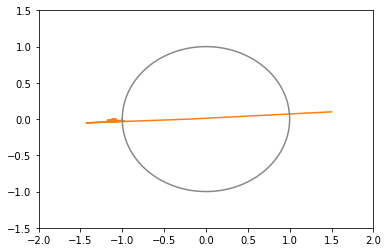
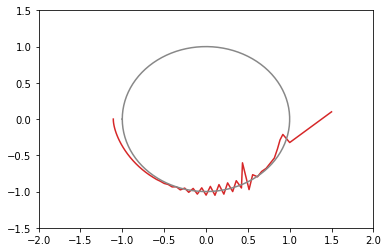
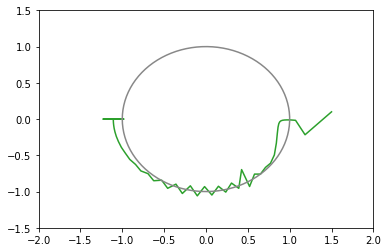
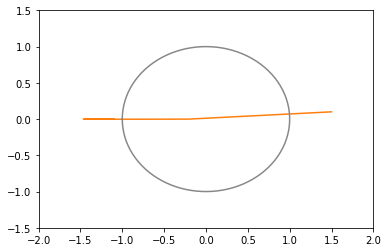
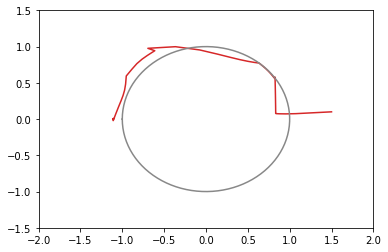
xy平面上での推移のグラフ（100回まで）（灰色の円は半径1の原点中心）

モーメンタム

opt1 = tf.optimizers.SGD(learning_rate=0.3, momentum=0.5) # 青: 発散
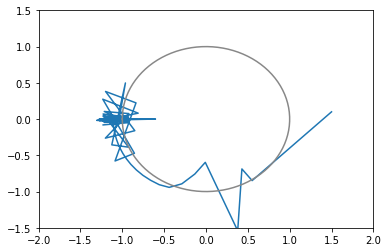
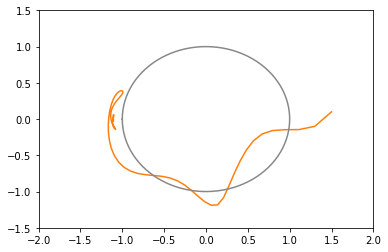
opt2 = tf.optimizers.SGD(learning_rate=0.2, momentum=0.5) # 橙: 20回で収束(下にxy図あり)
opt3 = tf.optimizers.SGD(learning_rate=0.1, momentum=0.5) # 緑: 27回で収束
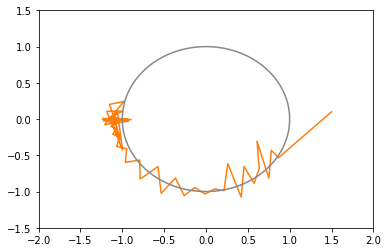
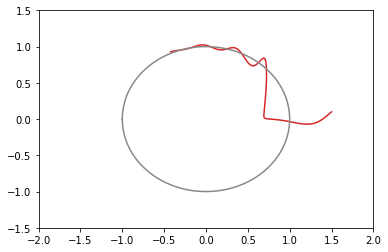
opt4 = tf.optimizers.SGD(learning_rate=0.05, momentum=0.5) # 赤: 103回で収束(下にxy図あり)

• モーメンタムがあると窪地は通り過ぎやすい
• 窪地を往復すると、モーメンタムがない場合にくらべ、早く発散するか早く収束する
• ゆるやかな坂道が続いてるときの収束は早い

損失関数の値の推移のグラフ

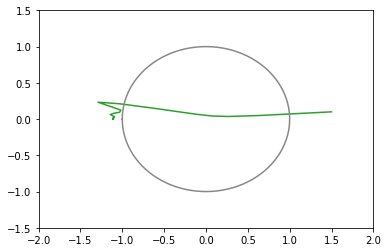
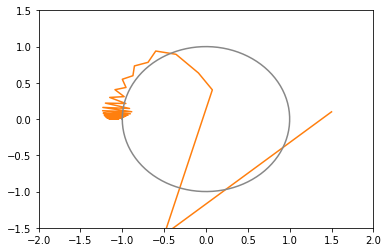
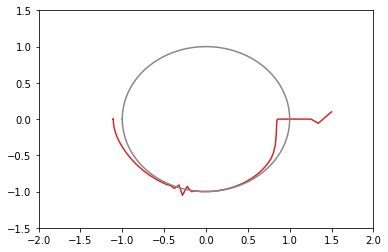
xy平面上での推移のグラフ（図が多いと貼るのが疲れるので一部のみ）

Nesterov加速法

使い方が違うのか tf.optimizers.SGD(learning_rate=0.1, nesterov=True) と書いても普通の勾配降下法となにも変わらなかった。

Adagrad

opt1 = tf.optimizers.Adagrad(learning_rate=3.0) # 青: 203回で収束
opt2 = tf.optimizers.Adagrad(learning_rate=2.0) # 橙: 104回で収束
opt3 = tf.optimizers.Adagrad(learning_rate=1.0) # 緑: 65回で収束
opt4 = tf.optimizers.Adagrad(learning_rate=0.5) # 赤: 73回で収束

たまに振動する。収束の閾値付近で振動すると、収束までに時間がかかる結果になる。

学習率 learning_rate は大きめの数字のほうがいいみたい。

損失関数の値の推移のグラフ

xy平面上での推移のグラフ

RMSprop

opt1 = tf.optimizers.RMSprop(learning_rate=0.3) # 青
opt2 = tf.optimizers.RMSprop(learning_rate=0.2) # 橙
opt3 = tf.optimizers.RMSprop(learning_rate=0.1) # 緑
opt4 = tf.optimizers.RMSprop(learning_rate=0.05) # 赤

学習率が大きいほど近づくのは早いけど、定期的に振動し、最適値付近でもピクピク動くので収束判定が難しい。

損失関数の値の推移のグラフ

xy平面上での推移のグラフ

Adadelta

opt1 = tf.optimizers.Adadelta(learning_rate=300) # 青
opt2 = tf.optimizers.Adadelta(learning_rate=200) # 橙 (下にxy図あり)
opt3 = tf.optimizers.Adadelta(learning_rate=100) # 緑
opt4 = tf.optimizers.Adadelta(learning_rate=50) # 赤 (下にxy図あり)

学習率 learning_rate のオーダーがずいぶんと違う。そして、どれも結局収束しない。

損失関数の値の推移のグラフ（他のOptimizerと違ってこれだけ300まで描画）

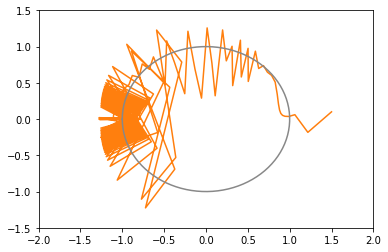
xy平面上での推移のグラフ（図が多いと貼るのが疲れるので一部のみ）

Adam

opt1 = tf.optimizers.Adam(learning_rate=0.3) # 青: 142回で収束
opt2 = tf.optimizers.Adam(learning_rate=0.2) # 橙: 148回で収束 (下にxy図あり)
opt3 = tf.optimizers.Adam(learning_rate=0.1) # 緑: 169回で収束
opt4 = tf.optimizers.Adam(learning_rate=0.05) # 赤: 231回で収束 (下にxy図あり)

ボールが転がり落ちるような動きをする。

損失関数の値の推移のグラフ

xy平面上での推移のグラフ（図が多いと貼るのが疲れるので一部のみ）

自作アルゴリズム

以下の私の記事で紹介した自作のアルゴリズムです。

• 勾配降下法の自作アルゴリズム

opt1 = CustomOptimizer(learning_rate=0.3) # 青: 7回で収束
opt2 = CustomOptimizer(learning_rate=0.2) # 橙: 9回で収束 (下にxy図あり)
opt3 = CustomOptimizer(learning_rate=0.1) # 緑: 52回で収束
opt4 = CustomOptimizer(learning_rate=0.05) # 赤: 53回で収束 (下にxy図あり)

2020/09/22追記：CustomOptimizerのソースコード → TensorFlowでOptimizerを自作する

学習率 learning_rate が大きいほど早く収束しますが、これ以上大きくしてもこれ以上は早くはならなかったです。それでも、学習率を大きくしすぎても発散はせずにすぐに収束します。

損失関数の値の推移のグラフ

xy平面上での推移のグラフ（図が多いと貼るのが疲れるので一部のみ）

リンク

TensorFlowのOptimizerのAPIレファレンス
Module: tf.keras.optimizers  |  TensorFlow Core v2.3.0

関連する私の記事

• 勾配降下法のアルゴリズム一覧のメモ
• 勾配降下法の自作アルゴリズム
• TensorFlowの自動微分を使って勾配降下法を試してみる