テキストに含まれた情報を有向グラフに変換する話（二）：依存構造グラフの章

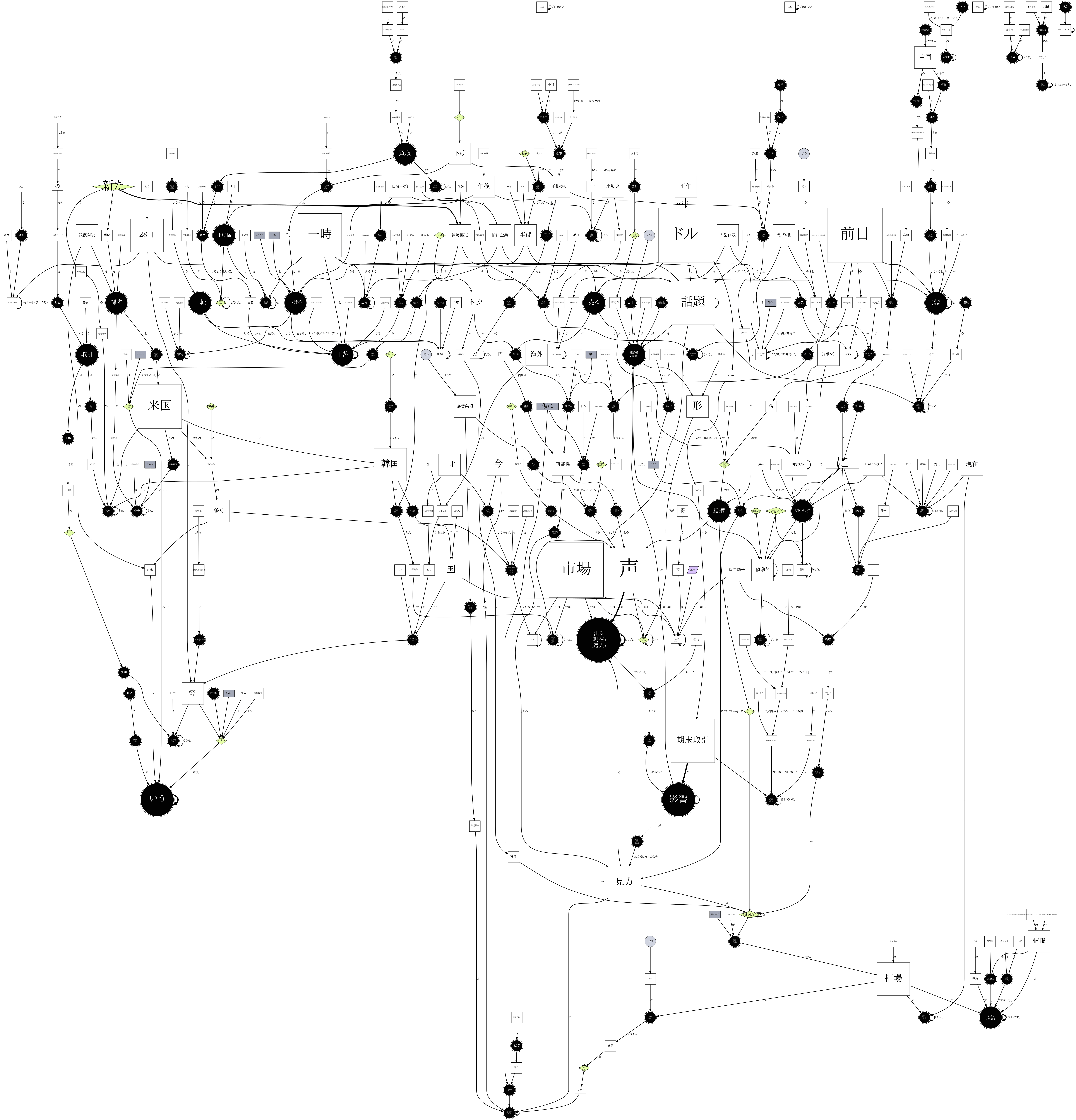
こんにちは。スーパーケロケロです。前回のテキストに含まれた情報を有向グラフに変換する話（一）：可視化の章で依存構造の可視化について紹介して、〔マーケットアイ〕外為：ドル105円半ばで小動き、実需筋の売り買い交錯というニュースからこのような有向グラフを生成するところまで行きました。今回はこのグラフに含まれた情報について考察していきます。

依存の木の特徴

いきなり膨大な図を見てもしょうがないので、まずは一つの文から生成された依存の木から考察しましょう。

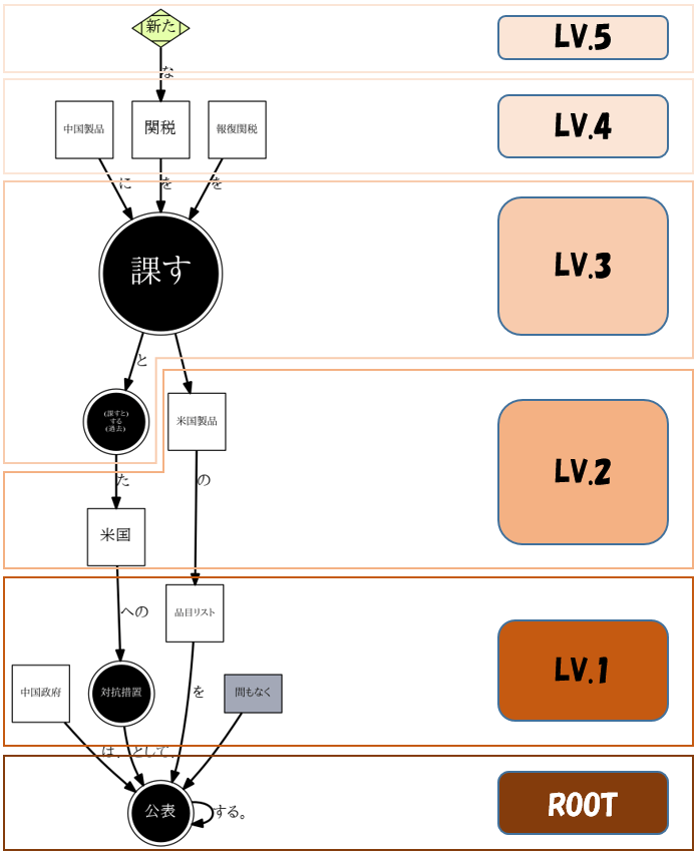
中国政府は、中国製品に新たな関税を課すとした米国への対抗措置として、報復関税を課す米国製品の品目リストを間もなく公表する。

レイヤー構造

　
依存の木のROOTを一番下に置き、更にROOTとの最短距離でレイヤーに番号を付けてみるとこんな感じになります。

直感的にもわかるように、生成された依存の木のレイヤー数は文の複雑度に比例する。この文の複雑度をレイヤーの数でみると 5 になります。

ROOTの”公表”はこの文が持つ意味の中核になっています。

ROOTからLV1まで遡ると、”中国政府は対抗措置として品目リストを間もなく公表する”という情報が得られます。これは公表というアクションの主体（中国政府）、客体（品目リスト）と付随情報（対抗措置、間もなく）を追加したという事です。

さらにLV2まで遡ると、ROOT客体（品目リスト）の付随情報（米国製品）とROOT付随情報（対抗措置）の付随情報（米国）が追加されます。

つまり、ROOTから遡れば遡るほど情報の粒度が細かくなります（より詳しくなる）。

依存の木が捉えている情報

テキストから依存の木に変換する時、依存の階層情報が抽出されると同時に、同じ階層のノード間の順番情報はなくなります。上の図のLV1を例としてみると、主体（中国政府）でも付随情報（対抗措置、間もなく）でも階層構造から見れば”平等”になっている。

主体客体などの相互関係情報がなくなるから、依存の木は完全な情報を取っていない。テキストから依存の木を生成できますが、依存の木から逆に正しい意味を持つテキストに復元する事はできない。

当然、複数の木から生成される依存構造グラフも元の意味を持つテキストに復元できない。ただ、グラフ生成時に一部の情報をあらかじめノードやエッジのメタ情報として取っていれば、のちにグラフ（の一部）からテキストに復元することが可能になります。

naruhodoを使って、一つ簡単な例を見よう：

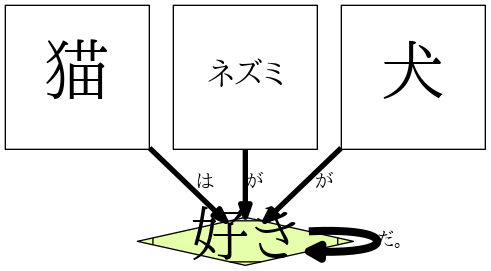
猫はネズミが好きだ。

ネズミは犬が好きだ。

犬は猫が好きだ。

以上の三つの文の意味を図で表せば直感的に三角形になると普通は思うでしょう。だが依存構造グラフにするとこうなってしまう：

# ライブラリーのインポート
from naruhodo import parser
# パーサ取得
dp = parser(lang='ja', gtype='d')
#
dp.add("猫はネズミが好きだ。")
dp.add("ネズミは犬が好きだ。")
dp.add("犬は猫が好きだ。")
# Jupyter Notebook　を使ている場合は　show()　で図を表示
# それ以外の場合は　plotToFile(filename="pic.png")
dp.show()

あれ、、、？！って感じでしょう。

テキストが持つ実際の意味をグラフのような構造化したデータに変換するというのは、知識表現
という人工知能研究の領域に属する。上記の猫・ネズミ・犬の三角情報を正確に捉える事ができるグラフがあれば、理論上それに基づいた問答システムや自動推論システムなどが作れるようになります。

こういった知識表現に関する人工知能研究は歴史が古く、1950年代ケンブリッジ言語研究所ユニットの意味ネットワーク（Semantic Network）から始まって、2000年前後にWWWの生みの親の一人ティム・バーナーズ＝リーによって提唱されたセマンティック・ウェブ（Semantic Web）、2012年にGoogleが発表したナレッジグラフ（Knowledge Graph）、2013年にCMUやUSCを含む複数の大学からの学者が提唱した抽象意味表現（Abstract Meaning Representation）など有名な例があります。さらに知識表現を指向したいくつかのプログラミング言語も存在する。比較的に有名なのはPrologとLisp。

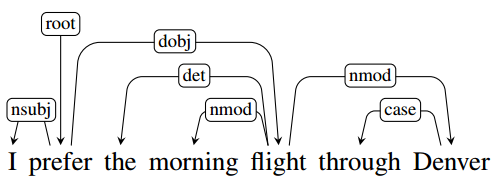
有効な情報は大抵の場合、実体と実体の関係や、実体にまつわるアクションや性質に関する記述なので、主体客体のような相互関係情報は必要不可欠です。英語の依存解析パッケージの多くは依存関係に加わって、親と子の間の相互関係もエッジの属性として与えられるタイプ情報付き依存構造（Typed dependency structure）を出力するが、日本語では依存関係（係り受け関係）だけ出力されるのが多い（CabochaやKNPなど）。

上の図はスタンフォード大学のCoreNLPのタイプ情報付き依存解析出力です。

naruhodoでは、依存構造と文節の機能語などの情報を利用して、前述の猫・ネズミ・犬の三角情報を正確に記述できる簡単な知識構造グラフを生成する機能も備えています。今回のテーマは依存構造グラフの考察なので、知識構造グラフに関してはまた次回で紹介します。

ここまで見れば、依存構造グラフに含まれる価値のある情報は、各ノードの相対階層分布によって表現される文章の情報粒度分布だと判る。　

次はこの方向に沿って依存構造グラフを解析してみる。

依存構造グラフの解析

naruhodoから生成されたグラフは有名なPythonグラフ処理ライブラリーnetworkxのDiGraphオブジェクトなので、networkxの機能を活用して解析していきましょう。

ノードの相対階層分布

まずは各ノードの平均階層を計算して、相対階層に応じて色を変化させてからグラフにしてみましょう。naruhodoを使えば、グラフ生成時に自動的にノードの平均階層を計算してくれます。

# グラフをリセットします
dp.reset()
# ウェブページをグラフに追加（取れたテキストは変数textsに保存）
texts = dp.addUrls("https://jp.reuters.com/article/tokyo-frx-idJPL3N1RA2SG")
# depth=Trueで相対階層情報付きのグラフを可視化する
dp.show(depth=True)

ノードがROOT（LV0）に近いほど色が濃くなります。これはある意味、情報粒度分布のヒートマップと考えられます。基本的には、文章の中に構造が複雑な長～い文が多ければ多いほど、グラフの薄い部分の割合が多くなります。

次は全ノードの平均階層を計算してみよう：

# カウンターを初期化
total = 0.
count = 0
# 全部のノードをループしてカウンターを加算する
for node, depth in dp.G.nodes(data="depth"):
    total += sum(depth)
    count += 1
# 平均値をプリント
print(total / count)

このニュースの平均ノード階層は3.24でした。自分が試したところ、ニュースによっては大体3～4くらいが普通だと思います。Wikipediaとかはやや大きくなる傾向があります。青空文庫の小説とかを解析して、作家ごとの数値を見比べてみたら面白いかもしれません。

ROOTの相対順位

依存文法の特性上、ROOTはほとんど述語ノードである。文ごとにROOTが存在しますが、では比較的に重要なのはどれになるのか？

今見ているのは依存構造のグラフだから、一番自然な考え方は依存されれば依存されるほどROOTの重要性が上がるだろう。この考え方に沿って、各ノードの依存度に関して数値化してみましょう。

やり方は何種類ありますが、一番シンプルで分かりやすいのはランダムウォークではないでしょうか。

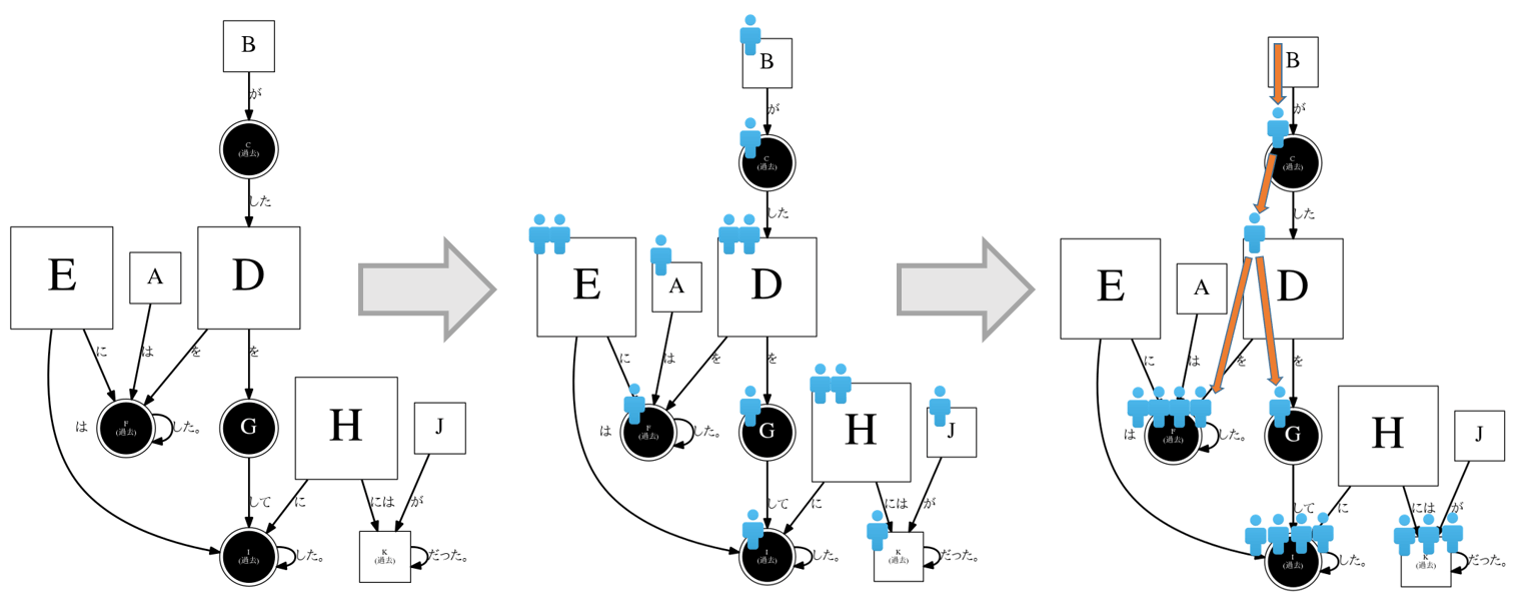
アルゴリズムは簡単に言うとこんな感じ：

• 始めはグラフ上の各ノードにエージェントを置く（数は重みに比例する）
• エージェントたちをグラフのエッジに沿って1ステップずつ動かす（移動先の確率はエッジの重みに比例する）
• 数回繰り返すとエージェント分布が安定になります。あとは各ノードにいるエージェントの数で重要性を決める

# ランダムウォークの遷移確率計算用関数
def getTProbs(G, node):
    lname = list()
    lsegs = list()
    for succ in G.successors(node):
        lname.append(succ)
        lsegs.append(G.edges[node, succ]['weight'])
    total = sum(lsegs)
    lsegs = [sum(lsegs[:i+1])/total for i in range(len(lsegs))]
    return lname, lsegs

# 乱数を生成してランダムウォークを実行する関数
from random import random
def randomWalk(lname, lsegs):
    rand = random()
    for i, seg in enumerate(lsegs):
        if rand <= seg:
            return lname[i]

# 各ノードのエージェント数辞書（demographics）と各ノードの遷移確率辞書（tprobs）の初期化
demographics = dict()
tprobs = dict()
for node, ct in dp.G.nodes(data="count"):
    demographics[node] = ct
    tprobs[node] = getTProbs(dp.G, node)
    tprobsR[node] = getTProbsR(dp.G, node)

# 100回ランダムウォークを実行する
for step in range(100):
    demographics_old = demographics.copy()
    for node in dp.G.nodes():
        for i in range(demographics_old[node]):
            if tprobs[node][0]:
                demographics[node] -= 1
                demographics[randomWalk(*tprobs[node])] += 1

# エージェント数上位10のノードを出力
top = sorted(demographics, key=lambda x:demographics[x], reverse=True)[:10]
for i, x in enumerate(top):
    print(i, x.replace("\n", ""), demographics[x], dp.G.nodes[x]['pos'])

前述のニュースで試した結果：

順位	ノード名	エージェント数	出現した文の番号
0	(見方が)ある	64	[17]
1	目立つ(現在)	42	[20]
2	表示(現在)	37	[45, 46]
3	少ない(否定)	31	[29]
4	(話題と)なる(現在)	26	[26]
5	(展開と)なる	22	[43]
6	下落	21	[23, 27]
7	(相場と)なる(現在)	16	[4]
8	(話題と)なる(過去)	15	[13]
9	活発化	14	[36]

多少ランダム性があるから実行時環境によって結果は変動しますが、ある程度回数を増やせばノード順位は安定する。では、順位TOP3ノードの元テキストを見てみよう：

print(texts[17])
print(texts[20])
print(texts[45], texts[46])

No.17: 今のところ、相場がこのニュースに反応している様子はないものの、仮に、日米ＦＴＡを結ぶこととなり、為替条項が盛り込まれた場合は「円売りが緩む可能性がある」との見方がある。

No.20: 前日海外市場序盤に１カ月ぶり高値となる１５０円半ばをつけた後に急反落、１４８円台後半へ１．６円程度売られた後に、１４９円後半へ切り返すなど荒い値動きが目立っている。

No.45, 46: 全スポットレートアジアスポットレート欧州スポットレート通貨オプションスポットレートスポットレート国内株式関連の情報は約20分遅れ、海外株式関連の情報は15分以上の遅れで表示しています。 為替情報は10分ごとに更新されており、約10分前の相場を表示しています。

うん、、、予想通り、くそ長～い文ばかりですね( o∀o)。しかも意味的に一番重要な文を抽出したわけではなく、あくまで依存構造的に一番繋がってた文のROOTが一番前に出てくる(￣ω￣;)。要約としても使えそうにありません。

余談ですが、ランダムウォークの考え方はGoogleのページランクアルゴリズムと本質的には同じです。networkxにはグラフからノードのページランクを計算する機能が入っており、簡単に使えます：

# ライブラリーのインポート
import networkx as nx
# ページランク計算
pr = nx.pagerank(dp.G)
# ソートして上位ノードをプリント
sorted_pr = sorted(pr, key=lambda x:pr[x], reverse=True)
for i in range(10):
    print(sorted_pr[i].replace("\n", ""), pr[sorted_pr[i]])

結果も大体同じです。

まとめ

今回は依存構造グラフについて考察してみました。結果から言うと依存構造グラフの主な有効情報は粒度分布くらいで、直接の応用は難しい┐(´-｀)┌。応用ごとに最適のグラフ構造が大きく変わります。例えば要旨・要約・キーワード抽出とかは共起関係グラフ（TextRank: Bringing Order into Text.）や構文構造グラフ(Multi-sentence compression: Finding shortest paths in word graphs)を利用すると効果がいい。依存構造グラフの実用性を発掘するまではいけなかったが、色々楽しめたので、個人的には悪くなっかたと思います。次回のテキストに含まれた情報を有向グラフに変換する話（三）：知識構造グラフの章では依存構造グラフに基づいて幾つかのルールを追加することで、意味の情報をちゃんと取ろうとする知識構造グラフを紹介します。

この 作品 は クリエイティブ・コモンズ 表示 - 継承 4.0 国際 ライセンスの下に提供されています。