ここではそれぞれのネットワークの成績を計算し、最も成績が良いネットワークを探します。
成績を計算(③)
四つあるInputの組を入力し、それぞれのOutput結果を元にそのネットワークの成績を出力します。
import math
xor_inputs = [(0.0, 0.0), (0.0, 1.0), (1.0, 0.0), (1.0, 1.0)]
xor_outputs = [ (0.0,), (1.0,), (1.0,), (0.0,)]
fitness_threshold = 3.9
best_genome = None
class FeedForwardNetwork(object):
def __init__(self, inputs, outputs, node_evals):
self.input_nodes = inputs
self.output_nodes = outputs
self.node_evals = node_evals
self.values = dict((key, 0.0) for key in inputs + outputs)
@staticmethod
def eval_genomes(genomes):
for genome_id, genome in genomes:
genome.fitness = 4.0
net = FeedForwardNetwork.create(genome)
for xi, xo in zip(xor_inputs, xor_outputs):
output = net.activate(xi)
genome.fitness -= (output[0] - xo[0]) ** 2
def activate(self, inputs):
for k, v in zip(self.input_nodes, inputs):
self.values[k] = v
for node, act_func, agg_func, bias, response, links in self.node_evals:
node_inputs = []
for i, w in links:
node_inputs.append(self.values[i] * w)
s = sum(node_inputs)
z = max(-60.0, min(60.0, 5.0 * (bias + response * s)))
self.values[node]=1.0/(1+math.exp(-z))
return [self.values[i] for i in self.output_nodes]
@staticmethod
def feed_forward_layers(inputs, outputs, connections):
required = FeedForwardNetwork.required_for_output(inputs, outputs, connections)
layers = []
s = set(inputs)
while 1:
c = set(b for (a, b) in connections if a in s and b not in s)
t = set()
for n in c:
if n in required and all(a in s for (a, b) in connections if b == n):
t.add(n)
if not t:
break
layers.append(t)
s = s.union(t)
return layers
@staticmethod
def required_for_output(inputs, outputs, connections):
required = set(outputs)
s = set(outputs)
while 1:
t = set(a for (a, b) in connections if b in s and a not in s)
if not t:
break
layer_nodes = set(x for x in t if x not in inputs)
if not layer_nodes:
break
required = required.union(layer_nodes)
s = s.union(t)
return required
@staticmethod
def create(genome):
connections = [cg.key for cg in genome.connections.values() if cg.enabled]
output_keys = [i for i in range(num_outputs)]
input_keys = [-i - 1 for i in range(num_inputs)]
layers = FeedForwardNetwork.feed_forward_layers(input_keys, output_keys, connections)
node_evals = []
for layer in layers:
for node in layer:
inputs = []
for conn_key in connections:
inode, onode = conn_key
if onode == node:
cg = genome.connections[conn_key]
inputs.append((inode, cg.weight))
ng = genome.nodes[node]
node_evals.append((node, 'sigmoid', 'sum', ng.bias, 1.0, inputs))
return FeedForwardNetwork(input_keys, output_keys, node_evals)
実際に計算をしているのはeval_genomeというメソッドでこの計算をするために他のメソッドが定義されています。
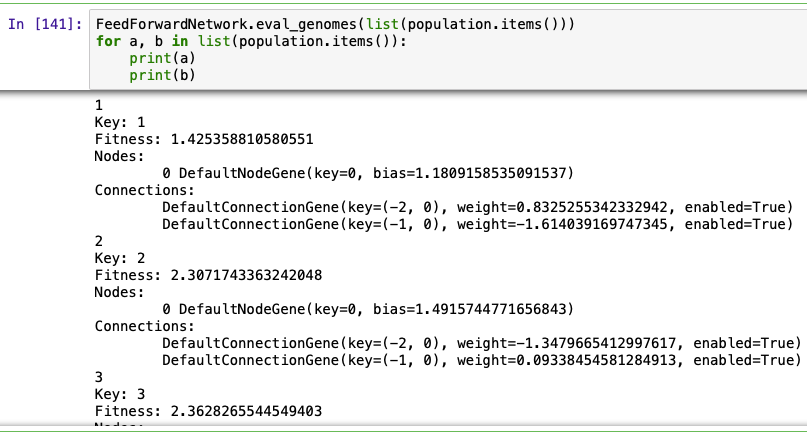
FeedForwardNetwork.eval_genomes(list(population.items()))
それぞれのネットワークのFitnessに数字が与えられている様子がわかります。この値は4に使いほど成績がよく、4から離れれば離れるほど成績が悪いと判断できます。
ここで、成績の出し方を説明します。
Fitness
例としてネットワーク(Key=1)の成績(Fitness)を計算したいと思います。
はじめにInput=0,0を入力して出力を計算すると、
\begin{align}
out(0, 0) &= Bias+0\times weight+0\times weight \\
&= Bias \\
&=1.181 \\
x &=5\times out(0, 0) \\
Fitness_{out(0,0)} &=1/(1+exp(-x)) \\
&=0.997
\end{align}
理想としてはout(0, 0)=0に近い方がいいので、今回の結果はいいとは言えません。また、1/(1+exp(-x))部分はsigmoid関数を表し、(0,1)の間に値をとります。
outに5をかけたのはパラメータのようなものなので変更可能です(今回はCodeReclaimersさんと同じように操作を進めたいと思います)。
他のInputも入力してみると、
\begin{align}
out(0, 1) &= Bias+0\times weight+1\times weight \\
&= Bias+1\times weight \\
&=1.181+(-1.614) \\
&=-0.433 \\
x &=5\times out(0, 1) \\
Fitness_{out(0,1)} &=1/(1+exp(-x)) \\
&=0.103 \\
out(1, 0) &= Bias+1\times weight+0\times weight \\
&= Bias+1\times weight \\
&=1.181+0.833 \\
&=2.014 \\
x &=5\times out(1, 0) \\
Fitness_{out(1,0)} &=1/(1+exp(-x)) \\
&=0.999 \\
out(1, 1) &= Bias+1\times weight+1\times weight \\
&=1.181+0.833+(-1.614) \\
&=0.4 \\
x &=5\times out(1, 1) \\
Fitness_{out(1,1)} &=1/(1+exp(-x)) \\
&=0.881 \\
\end{align}
今回の例をみると、Fitness(out(1, 0))は比較的理想とするOutputに近いのですが、それ以外は理想の値とはかなりかけ離れている様子がわかります。
そして、最後にFitnessを求めます。
\begin{align}
Fitness &= 4-((Fitness_{out(0,0)}-0)^{2} +(Fitness_{out(0,1)}-1)^{2} +(Fitness_{out(1,0)}-1)^{2}+(Fitness_{out(1,1)}-0)^{2}) \\
&=4-((0.997-0)^{2}+(0.103-1)^{2}+(0.999-1)^{2}+(0.881-0)^{2}) \\
&=1.425
\end{align}
実装結果とも同じ値になりました。
それぞれのFitnessから理想の値を引くことで得られる「誤差」を二乗して4から引きます。このように計算することによって、誤差が大きいほど成績が悪く、小さいほど成績が良いと判断することができます。つまりFitnessが4に近ければ成績は良く、4より小さいほど成績は悪いということです。今回の例だとFitnessが1.425と、4より小さいので成績はあまり良くありません。
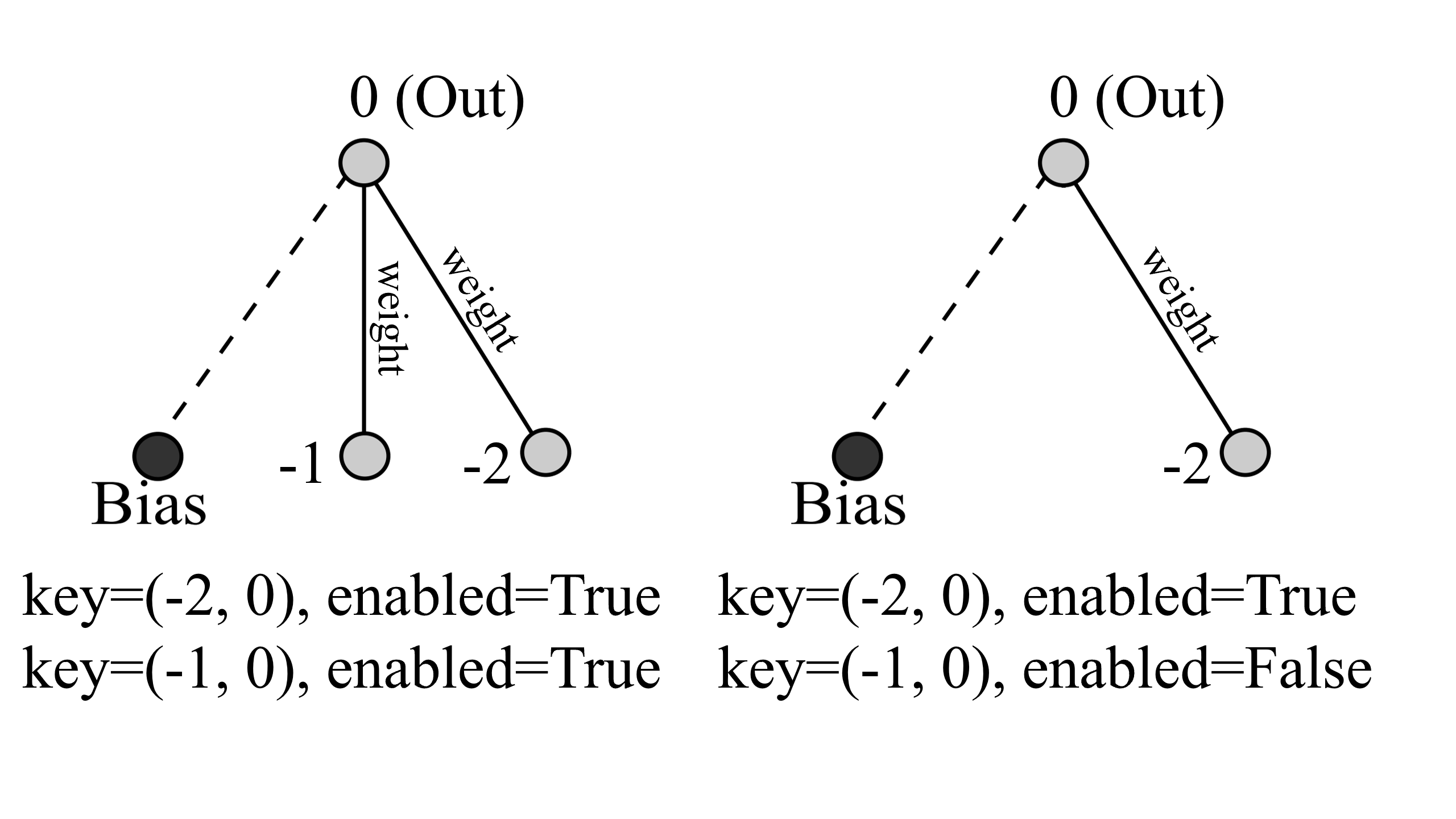
また、ConnectionsのenabledがFalseである場合は、Outputの計算過程が変わります。
下図右の例だとkey=(-1,0)のenabledがFalseなので、このConnectionsは Outputの計算には含まれません。
次は成績(Fitness)が最も良いネットワークを探します。
best = None
for g in population.values():
if best is None or g.fitness > best.fitness:
best = g
if best_genome is None or best.fitness > best_genome.fitness:
best_genome = best
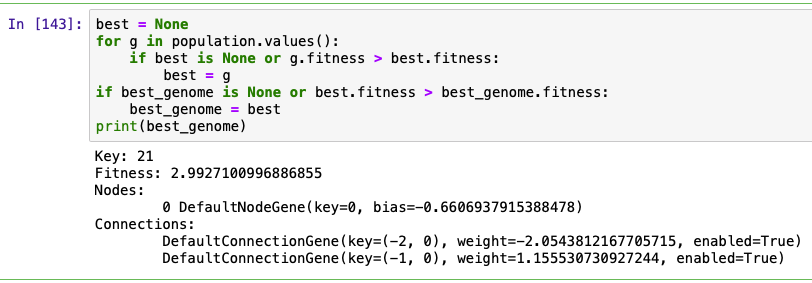
print(best_genome)
geenration=0において、150体あるネットワークのうち、最も成績が良かったのは、Key=21(21番目)のネットワークであることがわかりました。
しかし、そのFitnessの値をみると2.99と、4からは離れているのでこれでも精度がいいとは言えません。
次のコードを打ちます。
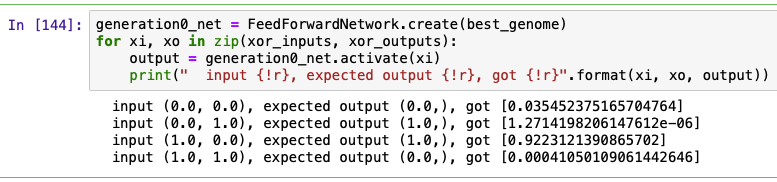
generation0_net = FeedForwardNetwork.create(best_genome)
for xi, xo in zip(xor_inputs, xor_outputs):
output = generation0_net.activate(xi)
print(" input {!r}, expected output {!r}, got {!r}".format(xi, xo, output))
最終的に得られた値(output)をみるとinput=(0, 1)のときの出力精度が良くありません。
世代を経るにつれ最終的にはFitnessが3.9(fitness_threshold)を上回るネットワークがあれば、そのネットワークが成績最優秀者として採用されます。
次回は交配を行い、突然変異を起こさせます。