VAEとEMアルゴリズムの違いについて

はじめに

情報系学部学生のsunです。この記事はEMアルゴリズムとVAE(変分オートエンコーダー）にMNIST（手書きの数字データセット）を学習させて、視覚的にアルゴリズムとしての違いを理解することを目的にしております。

注意

引用元は最後に記載しますが、コードの解説において、個人の解釈が間違っている場合があります。間違いを見つけた場合コメントにてお知らせくださいますと幸いです。

1章　全体的なイメージと違いについて

1-1

VAEのイメージから軽く触れたいと思います。

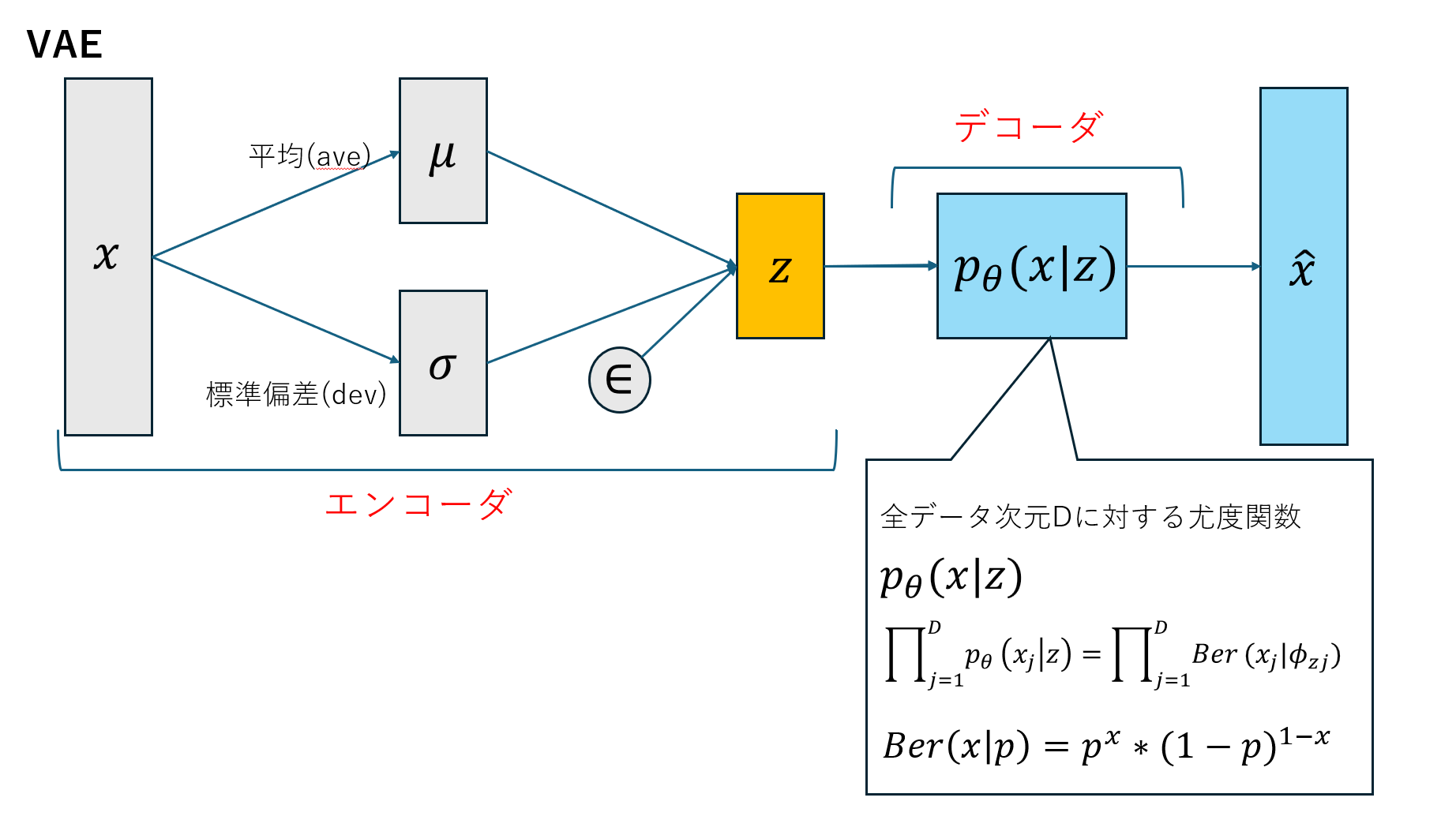
VAEとEMの比較をしたいと思います。
仮定として、MNISTの各ピクセル値がベルヌーイ分布に従うとします。

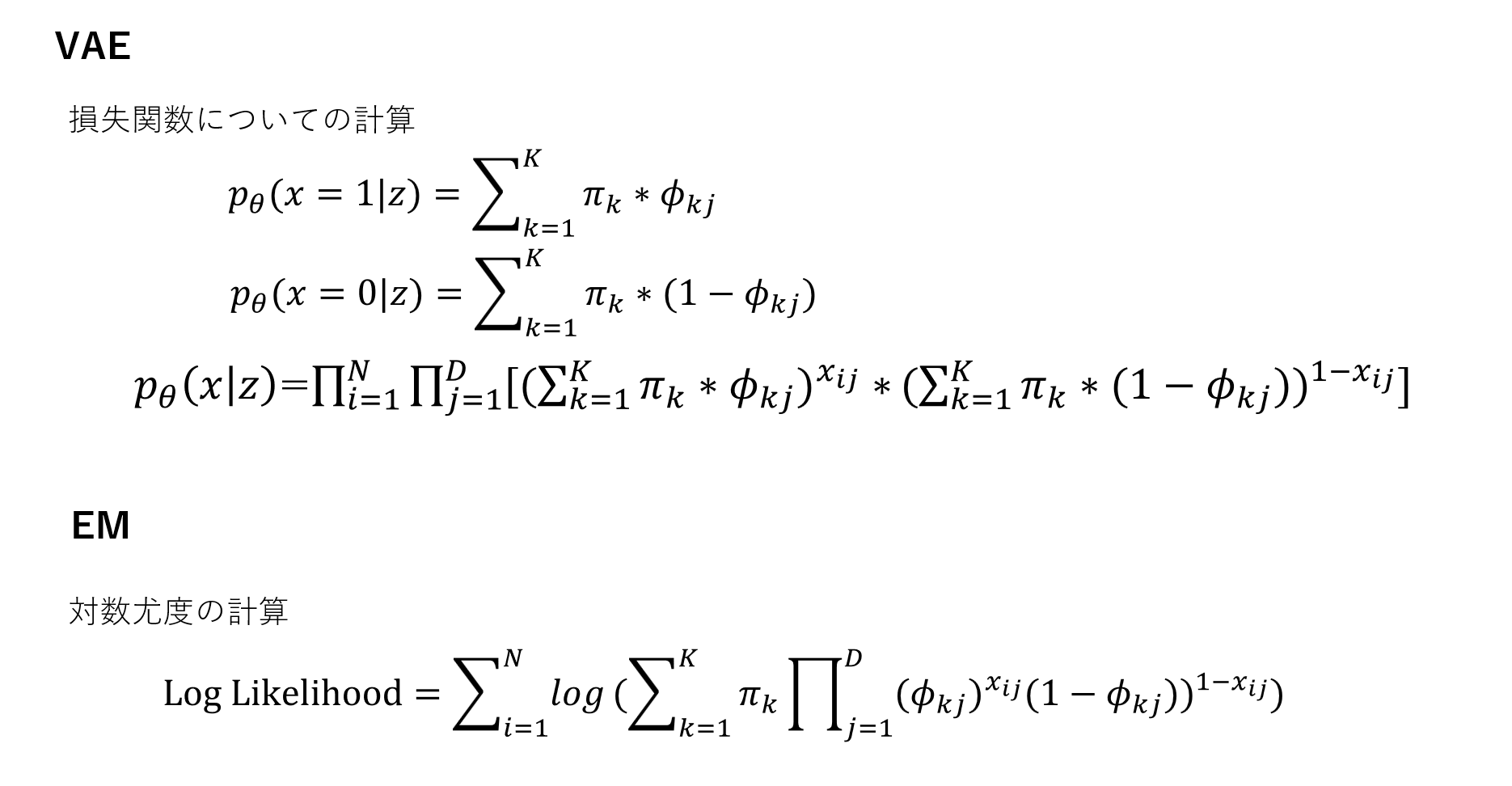
VAEのデコーダ部分と、EMアルゴリズムには数学的な構造に類似点があるように感じました。
なので、VAEとEMアルゴリズムを同じ条件下で手書き学習セットを学習させてみました。

1-2流れ

VAE

1.エンコーダの定義
2.デコーダの定義
3.損失関数の定義,トレーニング
4.収束

EMアルゴリズム

1.前置き
2.E-step,M-step
3.対数尤度の計算,収束判定（収束と結果）

1-3 イテレーションとエポックに関して

・VAE
一度のイテレーションで、ランダムにサンプリングされたバッチがモデルに共有されてパラメータを更新します。

・EM
一度のエポックでデータセット全体に対してE-stepとM-stepを繰り返します。これらは対数尤度が大きくなり、パラメータの変化もしくは、対数尤度の変化が小さくなるまでE-stepとM-stepを繰り返します。

1-4 可視化の方法について

・VAE：潜在空間での潜在変数の散布図をプロットしています。
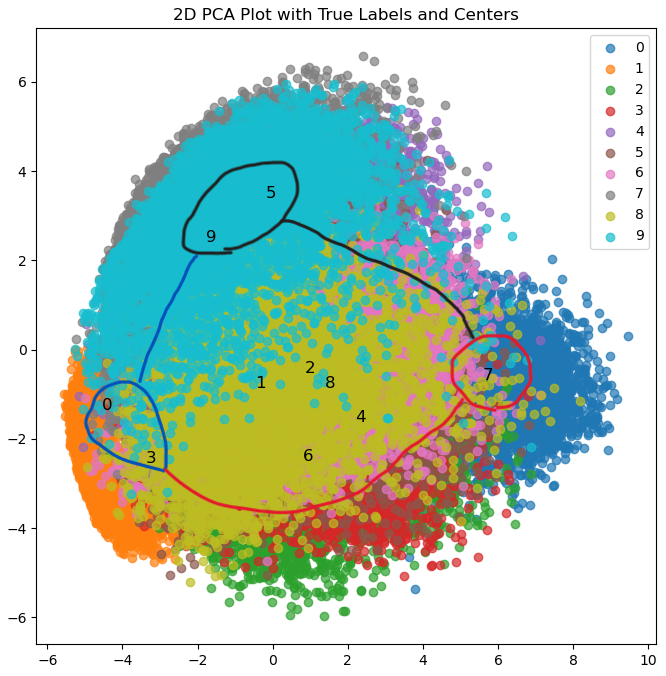
・EMアルゴリズム：主成分分析で次元削減した後にクラスタの中心とラベルを表示しています

1-5 VAEの誤差関数と混合ベルヌーイ分布の違いについて

VAEの誤差関数は再構築誤差とKLダイバージェンスを組み合わせた誤差関数が使用されます。
一方、混合ベルヌーイ分布を使うEMアルゴリズムでは複数のベルヌーイ分布から生成されたと仮定し、各分布が異なるクラスタをあらわすというものです。
両者の違いは、VAEは生成モデルとして潜在空間を学習することに対し、EMアルゴリズムはデータのクラスタリングに焦点を当てていることです。

2章　VAE

2-1　エンコーダ

encorder_detail_1.py

class Encoder(nn.Module):
  def __init__(self, z_dim): #クラスの初期化
    super().__init__()       #クラスの機能を継承
    self.lr = nn.Linear(28*28, 300)
    self.lr2 = nn.Linear(300, 100)
    self.lr_ave = nn.Linear(100, z_dim)   
    self.lr_dev = nn.Linear(100, z_dim)   
    self.relu = nn.ReLU()

self.lr：MNISTの画像のピクセル数が28*28であり、ピクセル一つ一つが特徴量として扱われ、その特徴量を300次元の特徴ベクトルに変換します。

・self.lr2：出力された300次元を線形変換により100次元に変換しています。ニューラルネットワークの中間層として機能しています。

・self.lr_ave：出力された100次元を潜在変数の次元数（z_dim）に線形変換します。エンコーダの中間層から潜在変数（z_dim）の平均を計算するための全結合層です。
→確率分布からサンプリングされた潜在空間内の点を表しています。

・self.lr_dev = nn.Linear(100, z_dim)：エンコーダの中間層から潜在変数（z_dim）の対数標準偏差を計算するための全結合層です。その後活性化関数を適用します。

encorder_detail_2.py

  def forward(self, x):
    x = self.lr(x)
    x = self.relu(x)
    x = self.lr2(x)
    x = self.relu(x)
    ave = self.lr_ave(x)    
    log_dev = self.lr_dev(x)    

    ep = torch.randn_like(ave)  
    z = ave + torch.exp(log_dev / 2) * ep  
    return z, ave, log_dev

・self.lr→relu：入力（x)に線形変換を適用し活性化関数を適用しています。

・self.lr2(x)：中間層から潜在変数の平均と対数標準偏差を計算するための線形変換を適用します。

・torch.randn_like(ave) ：平均0で分散1の正規分布に従う、与えられたテンソルと同じサイズの乱数epを生成します。

・ave + torch.exp(log_dev / 2) * ep ：再パラメータ化トリックを用いて潜在変数zを計算します。
→学習効率の向上

2-2　デコーダ

decorder_detail_1.py

class Decoder(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.lr = nn.Linear(z_dim, 100)
    self.lr2 = nn.Linear(100, 300)
    self.lr3 = nn.Linear(300, 28*28)
    self.relu = nn.ReLU()

・潜在変数の次元数を100次元に線形変換し、300次元に線形変換し、活性化関数を適用して元の28*28のMNISTの特徴量に変換します。

decorder_detail_2.py

 def forward(self, z):
    x = self.lr(z)
    x = self.relu(x)
    x = self.lr2(x)
    x = self.relu(x)
    x = self.lr3(x)
    x = torch.sigmoid(x) 
    return x

・torch.sigmoid(x)：MNISTのピクセル値の分布がベルヌーイ分布に近いと仮定し、最終的な出力にはシグモイド関数が適用され、0から1の範囲に値を設定し、ピクセルが白もしくは黒である確率を表しています。

2-3 VAE

vae_detail_1.py

class VAE(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.encoder = Encoder(z_dim)
    self.decoder = Decoder(z_dim)
  
  def forward(self, x):
    z, ave, log_dev = self.encoder(x)
    x = self.decoder(z)
    return x, z, ave, log_dev
    
def criterion(predict, target, ave, log_dev):
  bce_loss = F.binary_cross_entropy(predict, target, reduction='sum')
  kl_loss = -0.5 * torch.sum(1 + log_dev - ave**2 - log_dev.exp())
  loss = bce_loss + kl_loss
  return loss

  history = {"train_loss": [], "val_loss": [], "ave": [], "log_dev": [], "z": [], "labels":[]}

・F.binary_cross_entrop：PyTorchの関数で、バイナリクロスエントロピー誤差を計算します。
・predict:生成されたデータ、target：元データ（真のデータ）、reduction='sum'は損失の計算方法で、バッチ内のすべての要素の損失を合計して一つのスカラー値として返します。
→総合的な損失を得られます。

implementation_detail_1.py

history = {"train_loss": [], "val_loss": [], "ave": [], "log_dev": [], "z": [], "labels":[]}

・記載している変数を記録します。

implementation_detail_2.py

for epoch in range(num_epochs):
  model.train()
  for i, (x, labels) in enumerate(train_loader):
    input = x.to(device).view(-1, 28*28).to(torch.float32)
    output, z, ave, log_dev = model(input)

・for epoch in range(num_epochs):エポックを反復します。

・ model.train()：モデルを訓練モードに設定
・for i, (x, labels) in enumerate(train_loader):訓練データローダーからバッチごとにデータを取得。

・input = x.to(device).view(-1,28*28).to(torch.float32):x(入力データ）を指定したデバイスに移動し、28×28の形状に変換する。

implementation_detail_train.py

 loss = criterion(output, input, ave, log_dev)
 optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (i+1) % 50 == 0:
            print(f'Epoch: {epoch+1}, loss: {loss: 0.4f}')
        history["train_loss"].append(loss)

・loss:損失関数を計算します。vae_detail_2.pyで定義している関数により、再構築損失とKLダイバージェンス損失が組み合わさった総合的な損失が得られます。

・optimizer.zero_grad(),loss.backward(),optimizer.step()：勾配の初期化、逆伝播、オプティマイザを実行し、モデルを更新します。

・if (i+1) % 50 == 0:50バッチごとにエポックと損失を表示します。

implementation_detail_val.py

with torch.no_grad():
    for i, (x, labels) in enumerate(val_loader):
      input = x.to(device).view(-1, 28*28).to(torch.float32)
      output, z, ave, log_dev = model(input)

      loss = criterion(output, input, ave, log_dev)
      history["val_loss"].append(loss)
      
    print(f'Epoch: {epoch+1}, val_loss: {loss: 0.4f}')
    scheduler.step()

・with torch.no_grad():この文脈内では、勾配の計算は無効になっていて、推論のみが行われています。→計算の高速化、メモリ使用量の削減。

・訓練データと同様の動きを検証データでもう一度行います。

・ print(f'Epoch: {epoch+1}, val_loss: {loss: 0.4f}')：エポックごとの検証損失を表示します。

・scheduler.step()：モデルの収束やトレーニングの進捗に対して調整します。

2-5　収束と結果

・このグラフからちゃんと収束していることがわかる。

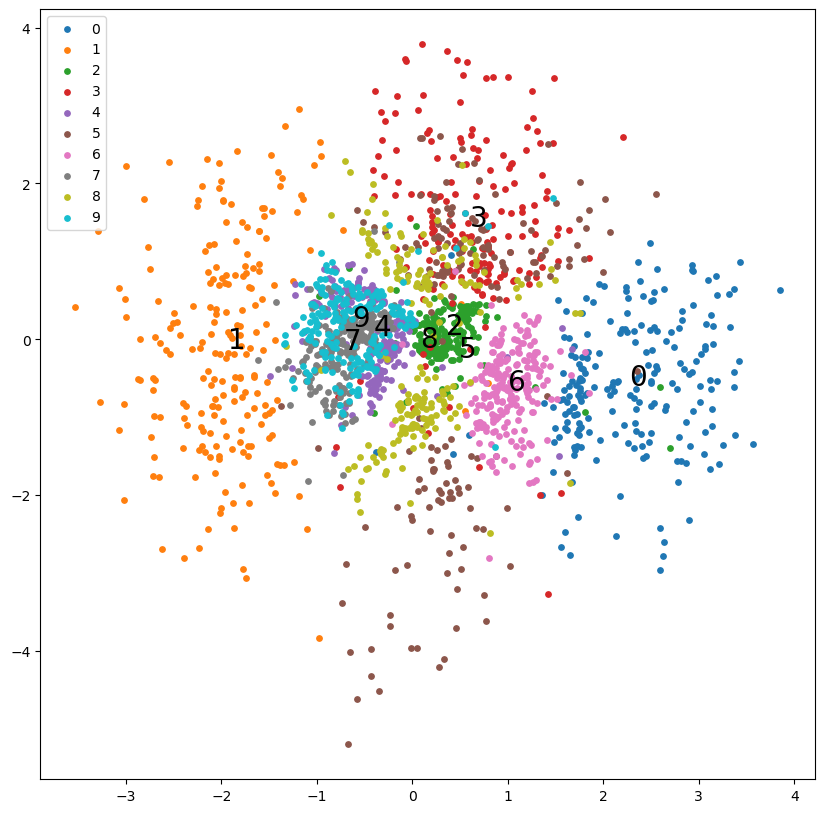
ここから潜在空間での潜在変数の散布図をプロットを書きます。

実行結果

plot_detail_2.py

batch_num = 9580
plt.figure(figsize=[10,10])
for label in range(10):
    x = z_np[batch_num:,:,0][labels_np[batch_num:,:] == label]
    y = z_np[batch_num:,:,1][labels_np[batch_num:,:] == label]
    plt.scatter(x, y, color=cmap(label/9), label=label, s=15)
    plt.annotate(label, xy=(np.mean(x), np.mean(y)), size=20, color="black")
plt.legend(loc="upper left")

実行結果

数字の通りラベルを付けて視覚的にわかる
https://github.com/sun5103/VAE-vs-EM

3章　EMアルゴリズム

3-1　前置き

import.py

%pylab inline
import numpy as np
import torch
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
from torchvision.datasets import MNIST, FashionMNIST
import pandas as pd
from sklearn.decomposition import PCA

load.py

train_dataset = datasets.MNIST('../data', train=True, download=True,transform=transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))]))

・train_dataset ：VAEと同様にMNISTデータセットをロードします。
また、画像をPyTrchのテンソルに変換し、正規化も行っています。また、画像のピクセル値が平均0.1307、標準偏差が0.3081になります。

Pre-processing.py

train_labels = train_dataset.train_labels.numpy()
train_data = train_dataset.train_data.numpy()
train_data = train_data.reshape(train_data.shape[0], -1)
def binarize(X):
    return 1 * (X >= 0.5)
bin_train_data = binarize(train_data)
bin_train_data = np.where(bin_train_data == 0,np.float32(0.0),np.float32(1.0))
# int32_elements = bin_train_data[np.where(bin_train_data.dtype == np.int32)]
# print(int32_elements)
assert bin_train_data.dtype == np.float32
assert bin_train_data.shape == train_data.shape

・train_labels,train_data：訓練データセットから取得したラベルと画像データをNumpy配列に変換しています。
そのあと、reshapeで二次元の行列を一次元に変換しています。
・bin_train_data:
binarize:入力されたxの行列の要素が0.5以上の場合は1に、それ以下の場合は0に変換します。
各ピクセルの値を0もしくは1にした後、浮動小数点数（32ビット）の形にしています。

・assert 文　正しいデータ型、形状を持っているかを確認しています。

この行では0と1の二つの値にデータセットを変換しています。

ここで、指定した数字に対するMNISTデータセットの画像と1と0で構成されている画像を見比べてみます。

Visual.py

def visualize_digit(digit, n_samples=4):
    idxs = np.random.choice(np.where(train_labels == digit)[0], n_samples)
    fig, ax = plt.subplots(nrows=1, ncols=2*n_samples, figsize=(20, 20))

    i=0
    for idx in idxs:
        img = train_data[idx].reshape(28, 28)
        bin_img = binarize(img)
        ax[i].imshow(img, cmap='gray')
        ax[i].set_title(str(digit), fontsize=16)
        ax[i].axis('off')
        ax[i+1].imshow(bin_img, cmap='gray')
        ax[i+1].set_title('Binarized '+str(digit), fontsize=16)
        ax[i+1].axis('off')
        i+=2
for digits in [1]:
    visualize_digit(digits)

・idxs：指定された数字に対応するMNISTデータセットの中からランダムに選ばれた複数のサンプルのインデックスを含む一次元のNumPy配列にしています。

・fig, ax ：一行二列の図を作成する設定をしています。

・for文:指定した数字に対応するデータセットのランダムなサンプルと、その0と1で構成されている画像を描画しています。

実行結果

3-2　EMアルゴリズム

E-step.py

def E_step(X, mu, pi):
    eps = 0.0001 
    gamma = np.exp(np.log(pi+eps) + np.dot(X ,np.log(mu.T+eps)) + np.dot((1 - X), np.log(1 - mu.T + eps)))    
    gamma /= gamma.sum(axis=1)[:, np.newaxis]
    return gamma

eps：0になることを避ける補正値
pi：混合比率
mu:各クラスタの平均
gamma：各データ点に対するクラスタへの所属確率を正規化し,
確率の合計が1になるように調整しています。

m-step.py

def M_step(X, gamma):
    N_m = gamma.sum(axis=0)
    pi = N_m / X.shape[0]
    mu = np.dot(gamma.T , X) / N_m[:, np.newaxis]
    return mu, pi

・N_m：各クラスタに対するデータポイントの負担率の合計を表す配列です。

・pi：各クラスタの事前確率を表す配列。各クラスタのデータポイントの割合を表しています。

・mu：各クラスタの平均を表す配列。各データポイントに対する重みつきの平均を計算しています。

EM.py

def EM(X, K, max_iter, threshold=1e-3, mu=None, pi=None):
    if mu is None: mu = np.random.uniform(low=.15, high=.85, size=(K, shape(X)[1]))
    if pi is None: pi = np.ones(K) / K

    log_likelihoods = [] 

    for i in range(1, max_iter+1):
        mu_old, pi_old = mu, pi

        gamma = E_step(X, mu, pi)
        mu, pi = M_step(X, gamma) 
        
        log_likelihood = np.sum(np.log(np.dot(gamma, mu) * X + np.dot((1 - gamma), (1 - mu)) * (1 - X)))
        log_likelihoods.append(log_likelihood)

    return gamma, mu, pi, log_likelihoods

・ log_likelihoods = [] ：尤度関数が収束するかを後に確認するために必要です。

・gamma：E-stepを呼び出して、各データポイントが各クラスタに属する確率である負担率行列を計算します。
・mu, pi：M-stepを呼び出して、新しい平均と事前確率を計算します。

plot.py

def plot_2d_pca_with_labels_and_centers(data, labels, centers, title):
    # Apply PCA to reduce the dimensionality to 2
    pca = PCA(n_components=2)
    data_pca = pca.fit_transform(data)

    plt.figure(figsize=(8, 8))
    for label in set(labels):
        indices = np.where(labels == label)
        plt.scatter(data_pca[indices, 0], data_pca[indices, 1], label=label, alpha=0.7)

    # Plot cluster centers with stars
    center_pca = pca.transform(centers)
    for i, label in enumerate(set(labels)):
        center_indices = np.where(labels == label)
        plt.scatter(center_pca[i, 0], center_pca[i, 1], marker='*', s=200, color=plt.cm.cividis(i / len(set(labels))), label=f'Cluster Center {i}')

    plt.title(title)
    plt.legend()
    plt.show()

def sample_labels_with_mu_pi(labels, epochs=100, K=None, mu=None, pi=None, true_pi_init=False):
    if K is None: K = len(labels)
    print('-'*60+'\nLabels {}、cluster　K = {}\n'.format(labels, K)+'-'*60+'\n')

    labels_idxs = np.isin(train_labels, labels)
    subset_train_labels = train_labels[labels_idxs]
    subset_train_data = bin_train_data[labels_idxs]

    pi_true = []
    for label in labels:
        n_labels = np.isin(train_labels, label)
        pi_true.append(n_labels.sum())
    print('true mixing coefficient: {}'.format(np.array(pi_true)/np.array(pi_true).sum()))
    if true_pi_init: pi = np.array(pi_true)
    
    print('\nState for progress')
    gamma, mu, pi ,log_likelihoods = EM(X=subset_train_data, K=K, max_iter=epochs, mu=mu, pi=pi)
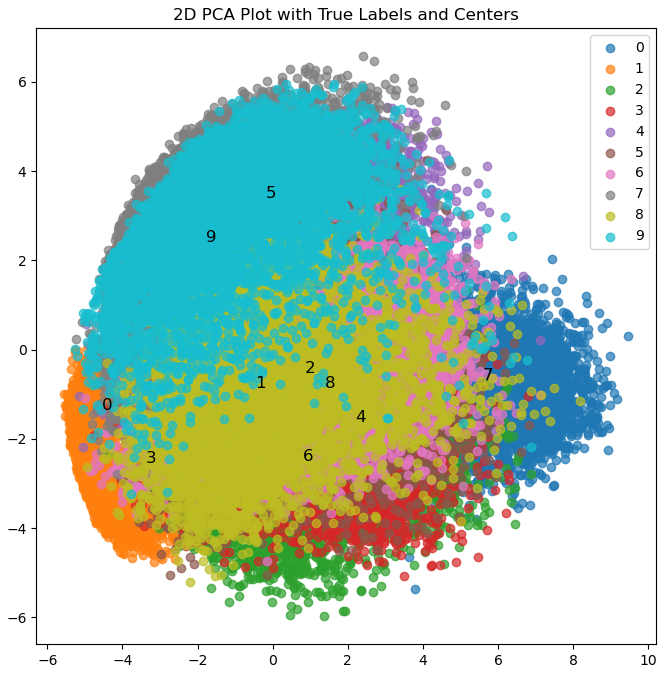
    plot_2d_pca_with_labels_and_centers(subset_train_data, subset_train_labels, mu, '2D PCA Plot with True Labels and Centers')

    return gamma, mu, pi, log_likelihoods

def plot_labels_with_centers_and_images(mu, labels, title):
    plt.figure(figsize=(15, 15))

    for i, center in enumerate(mu):
        plt.subplot(1, len(mu), i + 1)
        plt.imshow(center.reshape(28, 28), cmap='gray')
        plt.title(f'Cluster {i} - Label: {labels[i]}')
        plt.axis('off')

    plt.suptitle(title)
    plt.show()

gamma, mu, pi ,log_likelihoods = sample_labels_with_mu_pi([0,1,2,3,4,5,6,7,8,9])
plot_labels_with_centers_and_images(mu, [0, 1, 2, 3, 4, 5, 6, 7, 8, 9], 'Cluster Centers with Corresponding Labels')

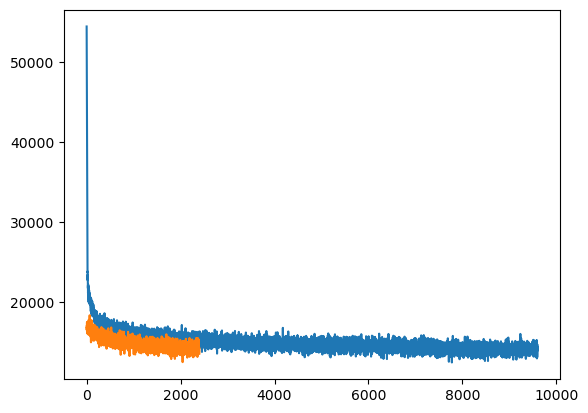
plt.plot(log_likelihoods, marker='o')
plt.title('Log Likelihood over Iterations')
plt.xlabel('Iteration')
plt.ylabel('Log Likelihood')
plt.show()

・784次元から2次元にするために主成分分析(PCA)で二次元に次元削減しています。

・次元削減したものをEMアルゴリズムを使いクラスタリングしています。

・クラスタの中心とそれに対応するラベルの画像を表示するために、関数内で定義しています

3-3　収束と結果

実行結果

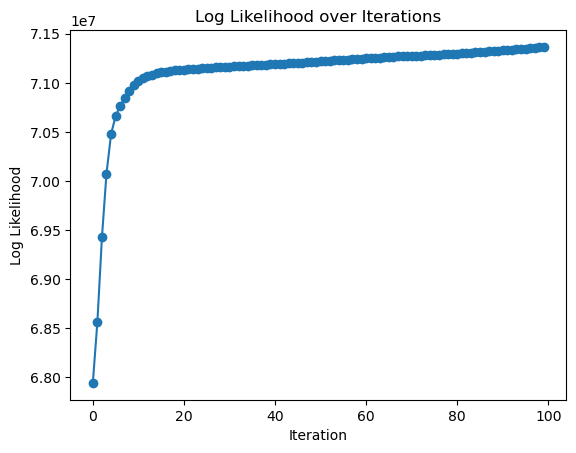
尤度関数が最大になるように対数尤度が変化しているので収束しているとわかります、

・クラスタリグ結果と対応したラベルの画像を表示しています。

4章　まとめ

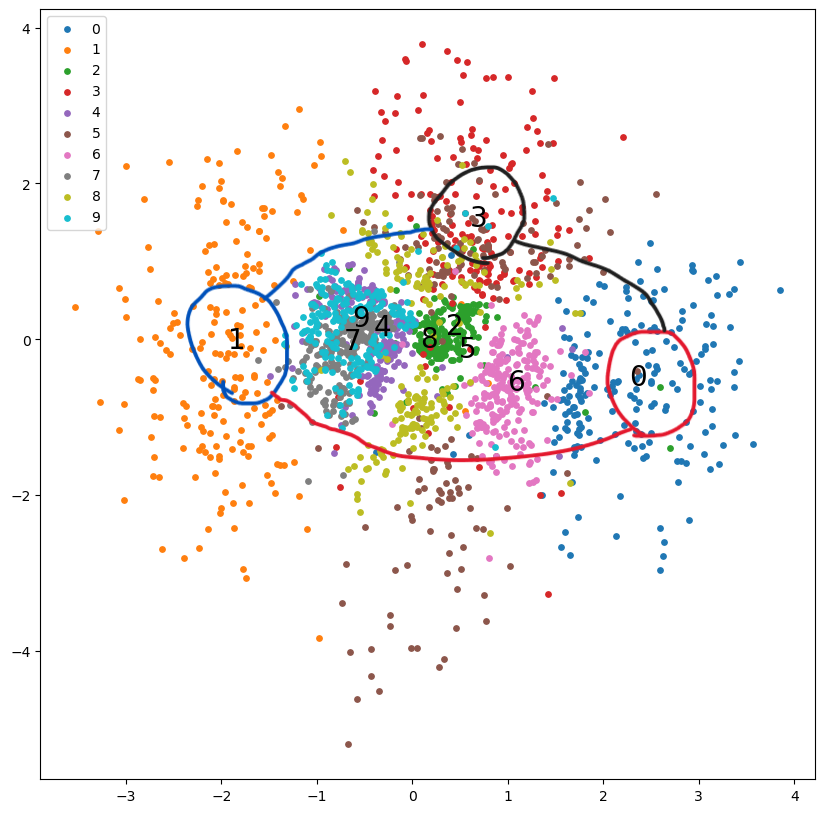
ここで、VAEで判別した画像とEMアルゴリズムで判別した画像を見てみたいと思います。
偏っている部分を囲み、そうでないものを線の内側になるように図に線を書いてみます。

VAE

EM

同じように囲むことができました。上の図だけ見るとVAEとEMアルゴリズムは同じような偏りがあることがわかります。

おまけ

今回扱ったEMアルゴリズムでは次元を削減してからEMアルゴリズムをしています。これはVAEと比べて大変な差があり、EMアルゴリズムはエンコーダの部分がないようなものなので、図自体は似ているように見えて、上記二つの図は全くの別のものになっています。
現在勉強中ではありますが、EMのほうでエンコーダを再現できるようなアルゴリズムがあればコメントのほうで知らせていただけると幸いです。
また、今回はEMアルゴリズムとVAEを理解している前提の記事になっておりますので、もし、EMやVAEの詳細を知りたい方はコメントしてください。

###　引用
https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
Variational Autoencoder徹底解説
https://github.com/ioangatop/machine_learning_2/blob/master/lab_3/12402559_12141666_lab3.ipynb
Lab 3: Expectation Maximization and Variational Autoencoder

参考

https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
PRML

・はじめてのディープラーニング2　著者：我妻 幸長