はじめに
自動微分と勾配テープでつまずいているので、調査しまとめることにしました。
主に以下のサイトを参考にしました。
公式より、「自動微分と勾配テープ」とは
TensorFlow には、自動微分、すなわち、入力変数に対する計算結果の勾配を計算するためのtf.GradientTape API があります。TensorFlow は、tf.GradientTape のコンテキスト内で行われる演算すべてを「テープ」に「記録」します。その後 TensorFlow は、そのテープと、そこに記録された演算ひとつひとつに関連する勾配を使い、トップダウン型自動微分(リバースモード)を使用して、「記録」された計算の勾配を計算します。
レポジトリはこちらです。
import
import tensorflow as tf
基礎
1回微分
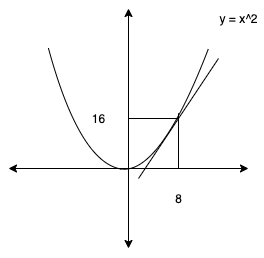
y = x^2
を微分して見ます。
\frac{dy}{dx} = 2x \\
\frac{dy}{dx} |_{x=8} = 16
操作は、このコンテキストマネージャー内で実行され、その入力の少なくとも1つが「監視」されている場合に記録されます。
x = tf.constant(8.0) # 8.0, shape=()
with tf.GradientTape() as t:
t.watch(x)
y = x * x
# 元の入力テンソル x に対する z の微分
dy_dx = t.gradient(y, x) # 16.0, shape=()
2回微分
y = x^2
を微分して見ます。
\frac{dy}{dx} = 2x \\
\frac{dy^2}{d^2x} = 2 \\
x = tf.constant(3.0) # 3.0, shape=()
print(x)
with tf.GradientTape() as t:
t.watch(x)
with tf.GradientTape() as tt:
tt.watch(x)
y = x * x
dy_dx = tt.gradient(y, x) # 6.0, shape=()
dy2_dx2 = t.gradient(dy_dx, x) # 2.0, shape=()
定数で微分できない場合
公式サイトによれば、微分できない場合は, '1' のテンソルを返すそうです。
x = tf.constant(8.0) # 8.0, shape=()
with tf.GradientTape() as t:
t.watch(x)
y = x
dy_dx = t.gradient(y, x) # 1.0, shape=()
制御フローの記録
勾配テープは演算を実行の都度記録するため、(たとえば if や while を使った)Python の制御フローも自然に扱われます。
def f(x, y):
output = 1.0
for i in range(y):
if i > 1 and i < 5:
output = tf.multiply(output, x)
return output
def grad(x, y):
with tf.GradientTape() as t:
t.watch(x)
out = f(x, y)
return t.gradient(out, x)
x = tf.convert_to_tensor(2.0)
grad(x, 6).numpy() # 12.0
勾配テープ内で使用するメソッド
テンソルのまま処理できます。
よく使うメソッド
reduce_sum = 配列内のすべての要素を足し算する関数
multiply = テンソルの要素の掛け算する関数
z = y^2 \\
\frac{dz}{dy} = 2x \\
\frac{dz}{dy} |_{x=4} = 8
より
\frac{dz}{dx}
= 8 \cdot \begin{bmatrix}
1 & 1 \\
1 & 1
\end{bmatrix}
=\begin{bmatrix}
8 & 8 \\
8 & 8
\end{bmatrix}
x = tf.ones((2, 2)) # x = [[1. 1.] [1. 1.]]
with tf.GradientTape() as t:
t.watch(x)
y = tf.reduce_sum(x) # 4.0, shape=()
z = tf.multiply(y, y) # 16.0, shape=()
dz_dx = t.gradient(z, x) # [[8. 8.] [8. 8.]], shape=(2, 2)
ループ
add = 関数の足し算
less = 未満の条件式
i = tf.constant(0)
c = lambda i: tf.less(i, 10)
# b = lambda i: (tf.add(i, 1), )
def b(i):
print(i)
return (tf.add(i, 1), )
r = tf.while_loop(c, b, [i])
tf.Tensor(0, shape=(), dtype=int32)
tf.Tensor(1, shape=(), dtype=int32)
tf.Tensor(2, shape=(), dtype=int32)
tf.Tensor(3, shape=(), dtype=int32)
tf.Tensor(4, shape=(), dtype=int32)
tf.Tensor(5, shape=(), dtype=int32)
tf.Tensor(6, shape=(), dtype=int32)
tf.Tensor(7, shape=(), dtype=int32)
tf.Tensor(8, shape=(), dtype=int32)
tf.Tensor(9, shape=(), dtype=int32)
Out[27]: (<tf.Tensor: shape=(), dtype=int32, numpy=10>,)
指定したインデックスを出力
gather_nd = テンソルと、そのテンソル内の位置を表すインデックスを提供します。指定したインデックスに対応するテンソルの要素を返します。第一引数は、探すテンソル、第二引数は、そのインデックスを指定します。
一次元配列の場合
x = tf.constant([0.1, 0.1, 1.5, 4.5, 3.6, 1.2])
y = tf.constant([3.1, 2.3, 1.4, 2.3, 4.4, 3.1])
uniqueIndices = tf.constant([0, 1, 2, 3, 4, 5])
x = tf.gather_nd(x, uniqueIndices[:,None])
y = tf.gather_nd(y, uniqueIndices[:,None])
tf.multiply(x, y) # shape=(6,), array([ 0.31 , 0.23 , 2.1 , 10.349999, 15.84 , 3.72 ])
array([ 0.31 , 0.23 , 2.1 , 10.349999, 15.84 , 3.72 ])
の間が空いているのは、その分のメモリを開けているからだと思われます。
二次元配列の場合
x = [[1,2,3],[4,5,6]]
y = tf.gather_nd(x, [[1,1],[1,2]]) # shape=(2,) numpy=array([5, 6], dtype=int32)
条件分岐
less = 大小比較のメソッド
cond = いわゆるif。条件分岐します。
x = tf.constant(2)
y = tf.constant(5)
def f1(): return tf.multiply(x, 17)
def f2(): return tf.add(y, 23)
r = tf.cond(tf.less(x, y), f1, f2)
rはf1()の値が設定されます。f2の操作(例:tf.add)は実行されません。
(x= 2, r = 34)
関数
公式より
tf.functionを用いてある関数にアノテーションを付けたとしても、一般の関数と変わらずに呼び出せます。一方、実行時にはその関数はグラフへとコンパイルされます。これにより、より高速な実行や、 GPU や TPU での実行、SavedModel へのエクスポートといった利点が得られます。
@tf.function
def mini_func(x):
return x * x
x = tf.constant(5.0)
with tf.GradientTape() as t:
t.watch(x)
result = mini_func(x)
dy_dx = t.gradient(result, x)
print(dy_dx) # tf.Tensor(10.0, shape=(), dtype=float32)
constantとVariableの違いについて
TensorFlowにおけるconstantとVariableの違いは、constantを宣言した場合、その値は将来的に変更できない(また、初期化は操作ではなく値で行う必要がある)ことです。
また、デフォルトでは、GradientTapeは、コンテキスト内でアクセスされるすべてのtrainable変数を自動的に監視します。(t.watch(v)しなくてよい。)
constantの場合
@tf.function
def mini_func(x):
return x * x
x = tf.constant(5.0)
with tf.GradientTape() as t:
t.watch(x)
result = mini_func(x)
dy_dx = t.gradient(result, x)
print(dy_dx) # tf.Tensor(10.0, shape=(), dtype=float32)
Variableの場合
@tf.function
def mini_func(x):
return x * x
x = tf.Variable(5.0)
with tf.GradientTape() as t:
result = mini_func(x)
dy_dx = t.gradient(result, x)
print(dy_dx) # tf.Tensor(10.0, shape=(), dtype=float32)
クリッピング
clip_value_min ≤ value ≤ clip_value_max の場合は value
または - value < clip_value_min の場合は clip_value_min
または - clip_value_max < value の場合は clip_value_max
t = tf.constant([[-10., -1., 0.], [0., 2., 10.]])
t2 = tf.clip_by_value(t, clip_value_min=-1, clip_value_max=1)
t2.numpy()
array([[-1., -1., 0.],
[ 0., 1., 1.]], dtype=float32)
-1 ≤ value ≤ 1 の場合は value
または - value < -1 の場合は -1
または - 1 < value の場合は 1
を満たす形になっていることがわかります。
tensorの操作
全て0のtensorを作る
tf.zeros([2, 3])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0., 0., 0.],
[0., 0., 0.]], dtype=float32)>
全て1のtensorを作る
tf.ones((2, 3))
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[1., 1., 1.],
[1., 1., 1.]], dtype=float32)>
全て同じ値のtensorを作る
tf.fill([2, 3], 9)
<tf.Tensor: shape=(2, 3), dtype=int32, numpy=
array([[9, 9, 9],
[9, 9, 9]], dtype=int32)>
キャスト
tf.float32に揃えていないことで、以下のエラー文が出ます。なので、揃っていない時は、揃えましょう。
InvalidArgumentError: cannot compute Mul as input #1(zero-based) was expected to be a float tensor but is a double tensor [Op:Mul]
labels = tf.constant([0, 3, 1])
print(labels)
tf.cast(labels, tf.float32)
tf.Tensor([0 3 1], shape=(3,), dtype=int32)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0., 3., 1.], dtype=float32)>
numpyに変換
tensorに慣れてないうちは、かなり使います。
labels = tf.constant([0, 3, 1])
print(labels)
labels.numpy()
tf.Tensor([0 3 1], shape=(3,), dtype=int32)
array([0, 3, 1], dtype=int32)