はじめに
初めてKaggle(カグル)のコンペに参加してみたお話です。
前回の「KaggleのTitanicで学習してみた」では、
ひと通り学習して提出するまでのステップを行いましたが、サンプルデータ(76%)に負ける結果になりました。
今回は「Titanicコンペ」でスコアをあげるため、データを精査したいと思います。
目次
1.相関関係について
2.変数の尺度
3.相関係数
4.Titanicの相関係数を調べる
5.結果
参考
履歴
1.相関関係について
前回は、学習データを適当にピックアップし「pclass」「sex」「Age」「fare」を利用して学習させました。
今回は学習に関連性のあるデータを、根拠をもって取捨選択したいと思います。
相関関係を確認するには散布図が有効です。
散布図は以下のようなグラフです。
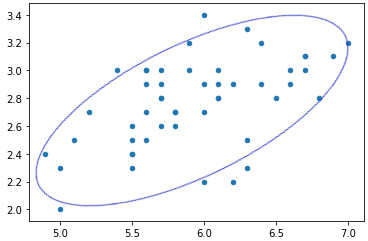
散布図が上記のようになった場合、右肩あがりの関連性があることが見て取れます。
例えば、横軸は身長、縦軸は体重である場合、身長が高い方が体重も重くなる傾向にあるので上記のような散布図になります。(なると思います。)
ただし、散布図は横軸、縦軸がともに量的変数の場合に有効です。
Titanicの「性別」(質的変数)と「生存」(質的変数)の散布図を作成する場合、
横軸の性別は「男性」「女性」の2種類、縦軸の生存は「0」と「1」の2種類になり、4つの点がだけの散布図になり、あまり意味がありません。
データの種類(量的変数、質的変数)によって、相関関係の調べ方が変わってきます。
2.変数の尺度
先ほど、量的変数、質的変数という言葉が出てきました。
扱うデータ(変数)は、性質により以下の尺度に分類されます。
| 変数の種類 | 尺度の種類 | 意味 | 例 |
| 質的変数 | 名義尺度 | 区別するために用いる尺度 | 性別、都道府県 |
| 順序尺度 | 大小関係にのみ意味がある尺度 | 順位、震度 | |
| 量的変数 | 間隔尺度 | 目盛が等間隔になっているもので、その間隔に意味があるもの | 気温、西暦 |
| 比例尺度 | 間隔と比率に意味があるもの(0が原点) | 身長、価格 |
散布図は比較対象が双方とも「量的変数」の場合に有効です。
「量的変数」と「順序尺度」の場合も有効だと思います。
片方が名義尺度の場合はあまり有効ではありません。
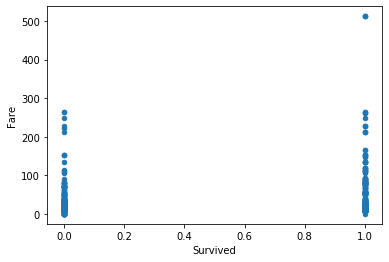
例えば、Titanicの「生存(0、1)」と「運賃」を散布図にプロットすると以下のようになります。
横軸(生存)が 0 と 1 の2値になり、相関がよく分かりません。
名義尺度の場合、散布図はあまり有効ではなさそうです。
散布図のほかに、相関関係は「相関係数」で表すこともあります。
こちらを見てみましょう。
3.相関係数
相関係数とは、2組のデータの間にどれほどの関係性があるのかを示す指標として使用されます。
numpyには、相関係数を求める関数があります。
numpy.corrcoef(x, y)[0, 1]
numpyのcorrcoefは正しくは「ピアソンの積率相関係数」と呼ばれます。
「ピアソンの積率相関係数」は後述する「量的変数」同士の相関関係に利用されます。
相関係数には他にも「クラメールの連関係数」や「相関比」があり、尺度により使い分けられたりしています。
変数の尺度と対応する相関係数をまとめてみました。
| 変数1 | 変数2 | 利用される相関係数 | Titanicの変数 |
| 名義尺度 | 名義尺度 | クラメールの連関係数 | 性別、チケット番号、客室番号、乗船港 |
| 順序尺度 | 順位相関比 | チケットクラス | |
| 量的変数 | 相関比 | 年齢、sibsp、parch、運賃 |
「クラメールの連関係数」と「相関比」のコードサンプルは以下です。「順位相関比」は相関比と大体同じだと思います。
import numpy
import pandas
######################################
# クラメールの連関係数
# Cramer's coefficient of association
# 0.5 >= : 非常に強い相関(Very strong correlation)
# 0.25 >= : 強い相関(strong correlation)
# 0.1 >= : やや弱い相関(Slightly weak correlation)
# 0.1 < : 相関なし(No correlation)
######################################
def cramersV(x, y):
"""
Calc Cramer's V.
Parameters
----------
x : {numpy.ndarray, pandas.Series}
y : {numpy.ndarray, pandas.Series}
"""
table = numpy.array(pandas.crosstab(x, y)).astype(numpy.float32)
n = table.sum()
colsum = table.sum(axis=0)
rowsum = table.sum(axis=1)
expect = numpy.outer(rowsum, colsum) / n
chisq = numpy.sum((table - expect) ** 2 / expect)
return numpy.sqrt(chisq / (n * (numpy.min(table.shape) - 1)))
######################################
# 相関比
# Correlation ratio
# 0.5 >= : 非常に強い相関(Very strong correlation)
# 0.25 >= : 強い相関(strong correlation)
# 0.1 >= : やや弱い相関(Slightly weak correlation)
# 0.1 < : 相関なし(No correlation)
######################################
def CorrelationV(x, y):
"""
Calc Correlation ratio
Parameters
----------
x : nominal scale {numpy.ndarray, pandas.Series}
y : ratio scale {numpy.ndarray, pandas.Series}
"""
variation = ((y - y.mean()) ** 2).sum()
inter_class = sum([((y[x == i] - y[x == i].mean()) ** 2).sum() for i in numpy.unique(x)])
correlation_ratio = inter_class / variation
return 1 - correlation_ratio
相関係数は -1 から 1 までの数字になります。
各計算式によって値の重みが変わってきます。
相関係数の値の目安は以下になります。
〇クラメールの連関係数、相関比
| 値 | 相関関係 |
|---|---|
| 0.5 >= | 非常に強い相関あり |
| 0.25 >= | 強い相関あり |
| 0.1 >= | やや弱い相関あり |
| 0.1 < | 相関なし |
〇ピアソンの積率相関係数
| 値 | 相関関係 |
|---|---|
| 0.7 >= | 非常に強い相関あり |
| 0.4 >= | 強い相関あり |
| 0.2 >= | やや弱い相関あり |
| 0.1 < | 相関なし |
相関係数のほかにも、名義尺度は「クロス集計」をグラフ化すると相関が分かる場合もあります。
4.Titanicの相関係数を調べる
それでは、Titanicの各変数について、相関係数とグラフで相関関係を見ていきましょう。
Titanicで「New NoteBook」を作成し、上記の「クラメールの連関係数」と「相関比」を定義します。
その後、以下のコードでトレーニングデータを読み込み準備します。
import matplotlib.pyplot as plt
# train.csvを読み込む
# Load train.csv
df = pandas.read_csv('/kaggle/input/titanic/train.csv')
##############################
# データ前処理
# 欠損値を処理する
# Data preprocessing
# Fill or remove missing values
##############################
# 年齢のNanを-1に変換する
# Convert age Nan to -1
df = df.fillna({'Age':-1})
# EmbarkedのNanを-1に変換する
# Convert Embarked Nan to -1
df = df.fillna({'Embarked':'null'})
##############################
# データ前処理
# ラベル(名称)を数値化する
# Data preprocessing
# Digitize labels
##############################
from sklearn.preprocessing import LabelEncoder
# 性別をLabelEncoderを利用して数値化する
# Digitize gender using LabelEncoder
encoder_sex = LabelEncoder()
df['Sex'] = encoder_sex.fit_transform(df['Sex'].values)
encoder_embarked = LabelEncoder()
df['Embarked'] = encoder_embarked.fit_transform(df['Embarked'].values)
Pclass(チケットクラス)
チケットクラスは「順序尺度」です。相関比で確認します。
######################################################
# データ分析 1
# Survived と Pclass(名義尺度)の相関関係を調べる
# Data analysis 1
# Examine the correlation between Survived and Pclass(nominal scale)
######################################################
CorrelationV(df['Survived'], df['Pclass'])
0.11456941170524215
「弱い相関あり」になりました。
クロス集計をグラフ化してみましょう。
cross_pclass = pandas.crosstab(df['Survived'], df['Pclass'])
cross_pclass.T.plot(kind='bar', stacked=True)
plt.show()
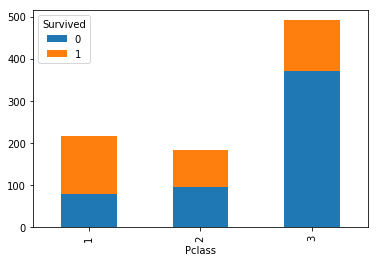
クラスが1の場合、生存「1」が5割を超えています。
クラスが3になると、生存「1」は1/4程度でしょうか。
相関係数は 0.1 と弱めですが、グラフをみるとまあまあ相関はありそうです。
Name(氏名)
氏名は今は飛ばします。
順番が前後しますが、本来は「データを観察する」ことも必要です。
氏名については、改めて取り上げる「データを観察する」回で触れたいと思います。
Sex(性別)
性別は「名義尺度」です。クラメールの連関係数で確認します。
######################################################
# データ分析 2
# Survived と Sex(名義尺度)の相関関係を調べる
# Data analysis 2
# Examine the correlation between Survived and Sex(nominal scale)
######################################################
cramersV(df['Survived'], df['Sex'])
0.5433513740027712
「非常に強い相関あり」になりました。
クロス集計をグラフ化してみましょう。
cross_sex = pandas.crosstab(df['Survived'], df['Sex'])
cross_sex.T.plot(kind='bar', stacked=True)
plt.show()
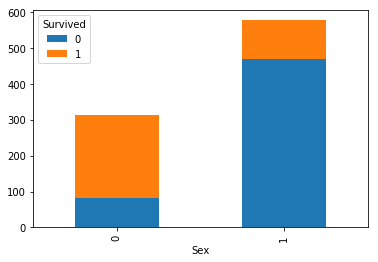
確かに男性、女性で大きく結果が異なっています。
Age(年齢)
年齢は「順序尺度」です。相関比で確認します。
######################################################
# データ分析 3
# Survived と Age(比例尺度)の相関関係を調べる
# Data analysis 3
# Examine the correlation between Survived and Age(ratio scale)
######################################################
CorrelationV(df['Survived'], df['Age'])
0.0001547299039139638
「相関なし」です。
クロス集計をグラフ化してみましょう。
10歳刻みでグラフ化します。
cross_age = pandas.crosstab(df['Survived'], round(df['Age'],-1))
cross_age.T.plot(kind='bar', stacked=True)
plt.show()
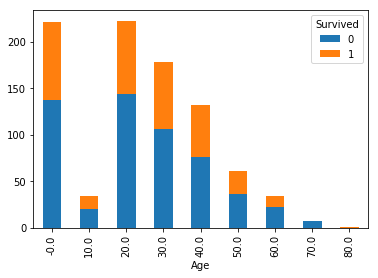
50代以降は生存「1」が少ない気がしますが、「相関なし」という結果です。
年齢がそれほど影響していないというのは意外でした。
SibSp(兄弟/配偶者の数)
SibSpは「量的変数(比例尺度)」です。相関比で確認します。
######################################################
# データ分析 4
# Survived と SibSp(比例尺度)の相関関係を調べる
# Data analysis 4
# Examine the correlation between Survived and SibSp(ratio scale)
######################################################
CorrelationV(df['Survived'], df['SibSp'])
0.0012476789275327471
「相関なし」です。
クロス集計をグラフ化してみましょう。
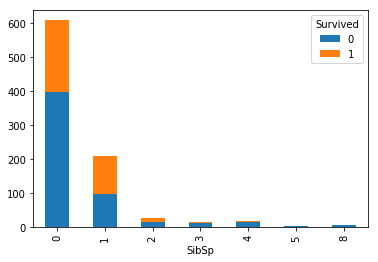
cross_age = pandas.crosstab(df['Survived'], df['SibSp'])
cross_age.T.plot(kind='bar', stacked=True)
plt.show()
グラフを見ても有意な相関は見て取れません。
Parch(親/子供の数)
Parchは「量的変数(比例尺度)」です。相関比で確認します。
######################################################
# データ分析 5
# Survived と Parch(比例尺度)の相関関係を調べる
# Data analysis 5
# Examine the correlation between Survived and Parch(ratio scale)
######################################################
CorrelationV(df['Survived'], df['Parch'])
0.006663360100801152
「相関なし」です。
クロス集計をグラフ化してみましょう。
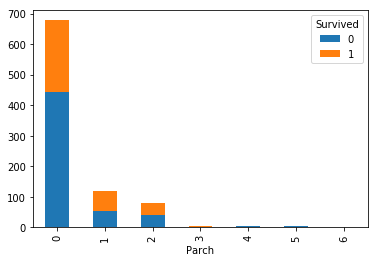
cross_age = pandas.crosstab(df['Survived'], df['Parch'])
cross_age.T.plot(kind='bar', stacked=True)
plt.show()
こちらも有意な相関は見て取れません。
Ticket(チケット番号)
チケット番号も今回は飛ばします。
こちらも、改めて取り上げる「データを観察する」回で触れたいと思います。
Fare(運賃)
運賃は「量的変数(比例尺度)」です。相関比で確認します。
標準化してから相関比を確認します。(標準化しなくても結果は同じになると思います)
##############################
# データ前処理
# 数値を標準化する
# Data preprocessing
# Standardize numbers
##############################
from sklearn.preprocessing import StandardScaler
# 標準化
# Standardize numbers
standard = StandardScaler()
df_std = pandas.DataFrame(standard.fit_transform(df[['Pclass', 'Sex', 'Fare']]), columns=['Pclass', 'Sex', 'Fare'])
# Fare を標準化
# Standardize Fare
df['Fare'] = df_std['Fare']
######################################################
# データ分析 6
# Survived と Fare(比例尺度)の相関関係を調べる
# Data analysis 6
# Examine the correlation between Survived and Fare(ratio scale)
######################################################
CorrelationV(df['Survived'], df['Fare'])
0.06620664646184327
「相関なし」です。
クロス集計をグラフ化してみましょう。
そのままだと、目盛りが細かくなりますので、0.2間隔でまとめます。
######################################
# -1.0 < x < -0.8 ⇒-1.0
# -0.8 < x < -0.6 ⇒-0.8
# -0.6 < x < -0.4 ⇒-0.6
# -0.4 < x < -0.2 ⇒-0.4
# -0.2 < x < 0 ⇒-0.2
# 0 < x < 0.2 ⇒ 0.0
# 0.2 < x < 0.4 ⇒ 0.2
# 0.4 < x < 0.6 ⇒ 0.4
# 0.6 < x < 0.8 ⇒ 0.6
# 0.8 < x < 1.0 ⇒ 0.8
# 1.0 < x ⇒ 1.0
######################################
def one_fifth(x):
if x < -0.8:
return -1.0
elif -0.8 <= x and x < -0.6:
return -0.8
elif -0.6 <= x and x < -0.4:
return -0.6
elif -0.4 <= x and x < -0.2:
return -0.4
elif -0.2 <= x and x < 0:
return -0.2
elif 0 <= x and x < 0.2:
return 0.0
elif 0.2 <= x and x < 0.4:
return 0.2
elif 0.4 <= x and x < 0.6:
return 0.4
elif 0.6 <= x and x < 0.8:
return 0.6
elif 0.8 <= x and x < 1.0:
return 0.8
else:
return 1.0
df['Fare_convert'] = df['Fare'].apply(one_fifth)
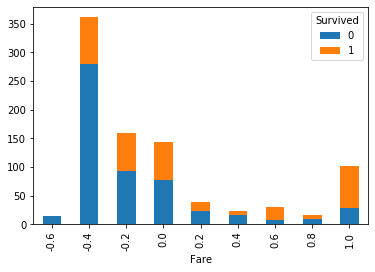
cross_age = pandas.crosstab(df['Survived'], df['Fare_convert'])
cross_age.T.plot(kind='bar', stacked=True)
plt.show()
fareが置きくなると、生存「1」が多くなっています。
係数は低いですが、相関はあるかもしれません。
Cabin(客室番号)
客室番号も今回は飛ばします。
こちらも、改めて取り上げる「データを観察する」回で触れたいと思います。
Embarked(乗船港)
乗船港は「名義尺度」です。クラメールの連関係数で確認します。
######################################################
# データ分析 7
# Survived と Embarked(名義尺度)の相関関係を調べる
# Data analysis 7
# Examine the correlation between Survived and Embarked(nominal scale)
######################################################
cramersV(df['Survived'], df['Embarked'])
0.18248384812341217
おしいですが、「相関なし」になりました。
クロス集計をグラフ化してみましょう。
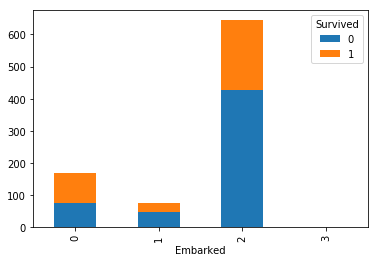
cross_embarked = pandas.crosstab(df['Survived'], df['Embarked'])
cross_embarked.T.plot(kind='bar', stacked=True)
plt.show()
相関があるような、ないような…。
5.結果
相関ありは、Pclass(チケットクラス)、Sex(性別)です。
Fare(運賃)も基準値には達しませんが、グラフでは少し相関がありそうです。
6.まとめ
相関関係および、クロス集計のグラフをもとにPclass(チケットクラス)、Sex(性別)、Fare(運賃)を入力パラメータとして利用したいと思います。
次はモデルの選別ですが、こちらは 次回 にします。
参考
様々な尺度の変数同士の関係を算出する(Python)
https://qiita.com/shngt/items/45da2d30acf9e84924b7
クラメールの連関係数の計算
https://qiita.com/canard0328/items/5ea4115d964b448903ba
履歴
2019/12/25 初版公開
2019/12/29 次回のリンク追加