様々な尺度の変数同士の関係を算出する(Python)

動機

相関係数など 2 変数の関係を表す指標が色々ありすぎて整理できないのと、尺度の組み合わせごとに整理してあるものも全ての組み合わせを網羅してなくてモヤっとするのでまとめてみる。正直あっているかどうかは自信ないので、気づいたことがあれば指摘してほしい。
最後のほう (ポリコリック相関係数とポリシリアル相関係数) は時間がなくて、ほぼ雰囲気のみで確認していないので動作は保証できない……

指標の種類

以下では水準数が9以上の順序尺度と水準数が2の質的変数(順序尺度・名義尺度)の一部は量的変数に含めている。

正規分布を仮定	変数の組み合わせ		使用する指標
している (パラメトリック)	量的変数	量的変数	ピアソンの積率相関係数
		順序尺度	ポリシリアル相関係数
		名義尺度	相関比 水準数 2 ならピアソンの積率相関可
	順序尺度	順序尺度	ポリコリック相関係数
		名義尺度	???
	名義尺度	名義尺度	??? (ここはない気がする)
していない (ノンパラメトリック)	量的変数 順序尺度	量的変数 順序尺度	スピアマンの順位相関係数
		名義尺度	順位相関比
	名義尺度	名義尺度	クラメールの連関係数

ピアソンの積率相関係数

いわゆる相関係数というとこれを指す。というか、これ以外の相関係数を知っている人のほうが世の中では少数派ではないだろうか。

$$
\displaystyle \frac
{\displaystyle \sum ^{n}_{i=1}\left(x _{i}-\overline{x}\right)\left(y _{i}-\overline{y}\right)}
{\sqrt{
\displaystyle \sum ^{n} _{i=1}\left(x _{i}-\overline{x}\right)^{2}
}\sqrt{
\displaystyle \sum ^{n} _{i=1}\left(y _{i}-\overline{y}\right)^{2}
}}
$$

np.corrcoef(x, y)[0, 1]

スピアマンの順位相関係数

ピアソンの積率相関係数の変数 $x,y$ に順位のデータを代入して整理したもの。 $x,y$ が量的変数であっても、非線形(ただし、単調増加・減少)の関係を捉えたり、外れ値の影響を取り除きたい場合には使ったりする。

$$
\displaystyle 1-\frac
{\displaystyle 6\sum^{n}_{i=1}(x _{i}-y _{i})^{2}}
{n^{3}-n}
$$

scipy.stats.spearmanr(x, y)[0][0, 1]

相関比

サンプルサイズを $n$ 、水準数を $c$ 、全体平均を $\overline{X}$ 、水準 (級、クラス) ごとの平均を $\overline{X} _{i}$ とすると

$$
\displaystyle \frac
{級間変動}
{全変動}
=\frac
{\displaystyle \sum ^{c} _{j=1} \sum _{i\in j}\left(\overline{X} _{j}-\overline{X}\right)^{2}}
{\displaystyle \sum ^{n} _{i=1}\left( x _{i}-\overline{X}\right)^{2}}
$$

分散分析 (ANOVA) のように偏差の平方和分解に基づいている。偏差平方和は変動のことであり、変動をサンプルサイズで割って平均を出したものが分散なので、全体の分散のうち水準の違いで説明できる部分の割合と考えられる。

$$
\begin{align}
\frac
{級間変動}
{全変動}
& =1-\frac
{級内変動}
{全変動}\
& \
& =1-\frac
{\displaystyle \sum ^{c} _{j=1} \sum _{i\in j}\left( x _{i}-\overline{X} _{j}\right) ^{2}}
{\displaystyle \sum ^{n} _{i=1}\left( x _{i}-\overline{X}\right) ^{2}}
\end{align}
$$

$x$ が量的変数、 $y$ が質的変数だとすると

variation = ((x - x.mean()) ** 2).sum()
inter_class = sum([((x[y == i] - x[y == i].mean()) ** 2).sum() for i in np.unique(y)])
correlation_ratio = inter_class / variation

順位相関比

ピアソンの積率相関係数とスピアマンの順位相関係数の関係のように、相関比の量的変数部分を順序尺度の変数にしたものが順位相関比。 (たぶん)

クラメールの連関係数

2 つの名義尺度同士に関係がない (独立)　とした場合に期待される観測数からの外れ具合を表した指数。
2 変数 (水準数は $k,l$ 、ただし $k \leqq l$) のクロス集計表を作成し、各水準ごとの観測数を $x _{ij}$ 、期待度数 (周辺度数) を $x _{i},x _{j}$ 、サンプルサイズを $n$ とすると

$$
\displaystyle \sqrt{
\frac
{\chi ^{2}}
{n(k-1)}
} =\sqrt{
\frac
{\displaystyle \sum ^{k} _{i=1}\sum ^{l} _{j=1}\frac
{x ^{2} _{ij}}
{x _{i} x _{j}}
-1}
{k-1}
}
$$

分割表 (クロス集計表) の $\chi ^{2}$ (カイ二乗) 値に基づいている。

	$1$	$2$	$\cdots$	$l$
$1$	$x _{11}$	$x _{12}$		$x _{1l}$	$\displaystyle x ^{(i)} _{1}=\sum ^{l} _{j=1} x _{1j}$
$2$	$x _{21}$	$x _{22}$		$x _{2l}$	$\displaystyle x ^{(i)} _{2}=\sum ^{l} _{j=1} x _{2j}$
$\vdots$			$\ddots$		$\vdots$
$k$	$x _{k1}$	$x _{k2}$		$x _{kl}$	$\displaystyle x ^{(i)} _{k}=\sum ^{l} _{j=1} x _{2j}$
	$\displaystyle x ^{(j)} _{1}=\sum ^{k} _{i=1} x _{i1}$	$\displaystyle x ^{(j)} _{2}=\sum ^{k} _{i=1} x _{i2}$	$\cdots$	$\displaystyle x ^{(j)} _{l}=\sum ^{k} _{i=1} x _{il}$	$\displaystyle n=\sum ^{k} _{i=1} \sum ^{l} _{j=1} x _{ij}$

$$
\begin{align}
\chi ^{2} & =\sum ^{k} _{i=1} \sum ^{l} _{j=1} \frac
{\left( 観測数-期待度数\right) ^{2}}
{期待度数}\
&\
& =\sum ^{k} _{i=1} \sum ^{l} _{j=1} \frac
{\displaystyle \left( x _{ij}-\frac
{x _{i}x _{j}}
{n}
\right) ^{2}}
{\displaystyle \frac
{x _{i}x _{j}}
{n}
}
\end{align}
$$

$x$ がpandas.crosstabなどを使ってクロス集計された結果 (ただし NumPy 配列) が入っているとすると

V = np.sqrt((x ** 2 / x.sum(axis=0, keepdims=True) / x.sum(axis=1, keepdims=True) - 1) / (min(x.shape)-1))

expected = scipy.stats.contingency.expected_freq(x)
chi2 = ((x - expected) ** 2 / expected).sum()
V = np.sqrt(chi2 / x.sum() / (min(x.shape) - 1))

chi2 = scipy.stats.chi2_contingency(x)
V = np.sqrt(chi2 / x.sum() / (min(x.shape) - 1))

ポリコリック相関係数

順序尺度の変数を、正規分布からサンプリングされた値を一定の閾値に基づいて順序尺度の変数にしたものと仮定し、元の正規分布 (二変量正規分布) での相関係数を求める。

例えば、閾値を $-1, 0, 1$ とすると、

	元の正規分布での値	順序尺度上での値
$x _{1}$	-2.3	1
$x _{2}$	-1.5	1
$x _{3}$	-0.8	2
$x _{4}$	0.1	3
$x _{5}$	0.5	3
$x _{6}$	1.3	4

つまり、閾値を $t _{1},t _{2},\cdots ,t _{r}$ とすると、順序尺度の値 $o _{1},o _{2}, o _{r+1}$ は $-\infty < o _{1} < t _{1} < o _{2} < t _{2} < \cdots < t _{r} < o _{r+1} < \infty$ という範囲の値を表す。

2 変数の値をそれぞれ $p _{1}, p _{2}, \cdots , p _{k}$ と $q _{1}, q _{2}, \cdots , q _{l}$ とする。
分割表 (クロス集計表) は以下の通り。

	$q _{1}$	$q _{2}$	$\cdots$	$q _{l}$
$p _{1}$	$x _{11}$	$x _{12}$		$x _{1l}$
$p _{2}$	$x _{21}$	$x _{22}$		$x _{2l}$
$\vdots$			$\ddots$	$\vdots$
$p _{k}$	$x _{k1}$	$x _{k2}$	$\cdots$	$x _{kl}$

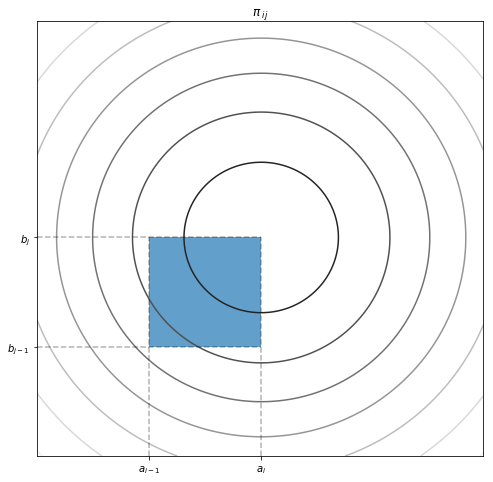
元の二変量正規分布からセル $x _{ij}$ の組み合わせが得られる確率を $\pi _{ij}$ とすると、このデータセットの尤度 $L$ (定数とかは省略) は

$$\displaystyle L=\prod ^{k} _{i=1}\prod ^{l} _{j=1} \pi ^{x _{ij}} _{ij}$$

対数尤度 $l$ は

$$\displaystyle l=\sum ^{k} _{i=1}\sum ^{l} _{j=1} x _{ij}ln\pi _{ij}$$

元の二変量正規分布の累積分布関数を $\Phi _{2} (a _{i},b _{j})$ とすると、

$$\displaystyle \pi _{ij} =\Phi _{2} ( a _{i} ,b _{j}) -\Phi _{2} ( a _{i} ,b _{j-1}) -\Phi _{2} ( a _{i-1} ,b _{j}) +\Phi _{2} ( a _{i-1} ,b _{j-1})$$

ただし、$a _{0} =b _{0} =-\infty,a _{k} =b _{l} =\infty$

ここで、閾値 $a_{i},b_{j}$ を周辺度数 (累積周辺分布) から推定してしまう。 (単変量) 標準正規分布の累積分布関数を $\Phi _{1} (z)$ (つまり、 $\Phi ^{-1} _{1} (z)$ がパーセント点)とすると、

$$
a _{i} =\Phi ^{-1} _{1} \left( \frac
{\displaystyle \sum ^{i} _{m=1} \sum ^{l} _{n=1} x _{mn}}
{\displaystyle \sum ^{k} _{m=1} \sum ^{l} _{n=1} x _{mn}}
\right)
$$

$$
b _{i} =\Phi ^{-1} _{1} \left( \frac
{\displaystyle \sum ^{k} _{m=1} \sum ^{j} _{n=1} x _{mn}}
{\displaystyle \sum ^{k} _{m=1} \sum ^{l} _{n=1} x _{mn}}
\right)
$$

from scipy.stats import norm
a = norm.ppf(x.sum(axis=0).cumsum() / x.sum())
b = norm.ppf(x.sum(axis=1).cumsum() / x.sum())

ここで対数尤度 $l$ を相関係数 $\rho$ で偏微分して $0$ とおいた

$$
\displaystyle \frac
{\partial l}
{\partial \rho }
=\sum ^{k} _{i=1} \sum ^{l} _{j=1} \frac
{x _{ij} }
{\pi _{ij} }
\left( \phi _{2}( a _{i} ,b _{j}) -\phi _{2} ( a _{i} ,b _{j-1} ) -\phi _{2} ( a _{i-1} ,b _{j} ) +\phi _{2} ( a _{i-1} ,b _{j-1} )\right) =0
$$

を解けばいいのだが、それは無理なのでscipy.optimize.minimizeを使って対数尤度を最適化する。

from scipy.stats import multivariate_normal
from scipy.optimize import minimize

k = a.size
l = b.size
a = [-np.inf] + a
b = [-np.inf] + a
bb, aa = np.meshgrid(b, a)
thresholds = np.empty(aa.shape + (2,))
thresholds[:, :, 0] = aa
thresholds[:, :, 1] = bb

def pi(rho):
    cov = np.eye(2)
    cov[0, 1] = cov[1, 0] = rho
    phi = multivariate_normal(cov=cov)
    return phi(thresholds[1:, 1:]) - phi(thresholds[:-1, 1:]) - phi(thresholds[1:, :-1]) + phi(thresholds[:-1, :-1])

def negative_log_likelihood(rho):
    return -(x * np.log(pi(rho))).sum()

rho = minimize(negative_log_likelihood, [0], bounds=((-1, 1)))

ポリシリアル相関係数

あまり情報が見当たらなかったが、おそらくポリコリック相関係数の片方の変数が量的変数 (正規分布) になったものだろう。

$p$ を量的変数、 $q$ を順序尺度の変数とする。
とりあえず、 $q$ の値に基づいてソートしておく。ついでに $p$ は標準化し、 $z$ とする。
$q$ は扱いやすいように $0$ から始まる整数にし、 $r$ とする。

z = (p[np.arg_sort(q)] - p.mean()) / p.std()
_, r, counts = np.unique(q, return_inverse=True, return_counts=True)

ポリコリック相関係数のときと同様に累積度数から閾値 $t$ を推定する。

from scipy.stats import norm
t = norm.ppf(list(counts.cumsum() / counts.sum()))
t = [-np.inf] + t

二変量正規分布
$$
\displaystyle \mathcal{N} \left( \left(
\begin{array}{ c }
\mu _{x}\
\mu _{y}
\end{array}
\right) ,\left(
\begin{array}{ c c }
\sigma ^{2} _{x} & \rho \sigma _{x} \sigma _{y}\
\rho \sigma _{x} \sigma _{y} & \sigma ^{2} _{y}
\end{array}
\right) \right)
$$
の $x$ が与えられたときの条件つき分布は
$$
\displaystyle \mathcal{N}\left( \mu _{y} +\frac
{\sigma _{y}}
{\sigma _{x}}
\rho ( x-\mu _{x}) ,\left( 1-\rho ^{2}\right) \sigma ^{2} _{y}\right)
$$
なので、 $p$ が与えられたときの $q$ の分布は
$$
\displaystyle \mathcal{N}\left(\frac
{\rho ( x-\mu _{p})}
{\sigma _{p}}
,1-\rho ^{2}\right)
$$
で表される。
標準化した $z$ を使えば
$$
\displaystyle \mathcal{N}\left(\rho z,1-\rho ^{2}\right)
$$
なので、 $r$ のそれぞれの値がサンプリングされる確率は
$$
\pi _{r|z}=\Phi _{1}(t _{i+1})-\Phi _{1}(t _{i})
$$
尤度 $L$ は
$$
L=\prod ^{n} _{i=1}\phi _{1}(z _{i})*\pi _{r _{i}|z _{i}}
$$
対数尤度 $l$ は
$$
l=\sum ^{n} _{i=1}\left( ln(\phi _{1}(z _{i}))+ln(\pi _{r _{i}|z _{i}})\right)
$$

def negative_log_likelihood(rho):
    d = norm(loc=rho * z, scale=np.sqrt(1 - rho ** 2))
    return - np.log(norm.pdf(z)).sum() - np.log(d.cdf(t[r + 1]) - d.cdf(t[r])).sum()

これを最適化する。

from scipy.optimize import minimize
rho = minimize(negative_log_likelihood, [0], bounds=((-1, 1)))