pythonでヤコビアンや偏微分をやってみた

pythonで数式にはまってしまった

今学んでいることがpythonでいろいろやってみたらとても面白くて、記事にするのを忘れてしまいました。
pythonって代入や、因数分解、微分などいちいちコードで書く必要ないんですね。ライブラリ便利すぎ。大学の選択科目でカオス理論の初歩の初歩的なものや多変量解析の重回帰分析や、多変量正規分布などを今学んでおりますが、座学でよくわからない記号を眺めても何もわからないということで可視化してやるぞー。理論は全然わからんけど、見れば何かしら理解を得るきっかけとなるかも。多変量解析や微分方程式などを使うカオス理論は余りにも難しすぎるので、というか初めから躓いているので、今回はネットで初歩の初歩から解析学の方を中心にいろいろ検索してどれが理想のコードなのかを探ってきました。難しい言葉言っておいて、何も理解していないイキリですね...いつか多変量解析の理論を理解してコードをかけるようになりたい。そういや、何も理解してないのに何でこんなにやる気出てしまったのだ?

プログラムコード　基本的なライブラリ

pythonでsympyで機能をimportしました。ライブラリあざます。
微分がこんなに直感で表示されるなんて...とっても便利
コードを見れば分かると思いますが微分を使う機能はdiff()です

import sympy as sym
from sympy import *      # sympyライブラリから全ての機能をimoprt
sym.init_printing()      # 出力を整形

x=Symbol('x')                  # 文字'x'を変数xとして定義
y=Symbol('y')                 # 文字 'y'を変数yとして定義


#微分
a=diff(sin(x),x)  #sin(x)の微分
b=diff(exp(x),x)   # e^xの微分

# 高階微分
c=diff(x**4+x**3,x,2)  # x^4+x^3の2階微分


#偏微分
d=diff(x**2+x*y+2*y**2,x)  # x^2+xy+2y^2のxによる偏微分
e=sym.integrate(x+2*y,(x,0,2),(y,2,3))
print('a: {0}'.format(a))
print('b: {0}'.format(b))
print('c: {0}'.format(c))
print('d: {0}'.format(d))
print('e: {0}'.format(e))

上から順番に

cos(x)\\
e^x\\
6x(2x + 1)\\
2x+y\\
12

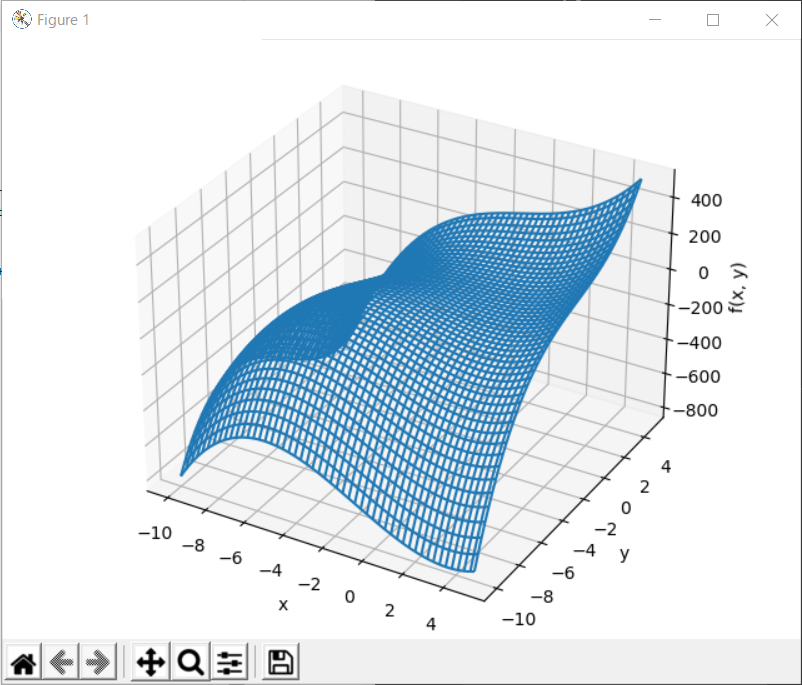
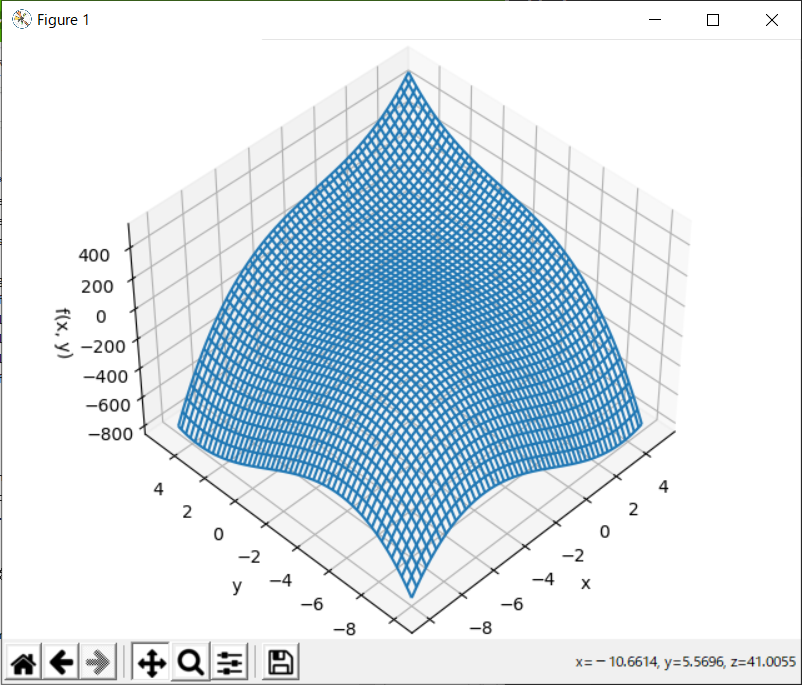
二変数関数のグラフ表示

{3x^2+6xy+3y^2+x^3+y^3}

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
def func1(x, y):
    return 3*x**2+6*x*y+3*y**2+x**3+y**3
x = np.arange(-10.0, 5.0, 0.1)
y = np.arange(-10.0, 5.0, 0.1)
X, Y = np.meshgrid(x, y)
Z = func1(X, Y)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("f(x, y)")
ax.plot_wireframe(X, Y, Z)
plt.show()

わざわざめんどくさい停留点や極大点を手計算で求めたら極大値の点は(-4,-4)の場所にあるらしい。なんてわかりずらい。あってるのかな

極小値極大値を求める

from sympy import *


x = Symbol('x')

y = Symbol('y')



f =3*x**2+6*x*y+3*y**2+x**3+y**3




f_x = Derivative(f,x).doit() #xで1階偏微分

f_y = Derivative(f,y).doit() #yで1階偏微分



stationary_points = solve([f_x,f_y],[x,y]) #関数の停留点

stationary_points = list(map(lambda x:simplify(x),stationary_points)) #簡単化



f_xx = Derivative(f, x, 2).doit() #xで2階偏微分

f_yy = Derivative(f, y, 2).doit() #yで2階偏微分

f_xy = Derivative(f_x,y).doit() #xで偏微分してからyで偏微分

f_yx = Derivative(f_y,x).doit() #yで偏微分してからxで偏微分



#ヘッセ行列

hesse = Matrix([

[f_xx,f_xy],

[f_yx,f_yy]

])



#ヘッセ行列の行列式

det_hessian = hesse.det()



#とりあえず出力

print('f_x: {0}'.format(f_x))

print('f_y: {0}'.format(f_y))

print('f_xx: {0}'.format(f_xx))

print('f_yy: {0}'.format(f_yy))

print('f_xy: {0}'.format(f_xy))

print('f_yx: {0}'.format(f_yx))

print('全ての停留点は {0}'.format(stationary_points))



#判定

for i in range(len(stationary_points)):

    sign_det_hessian = det_hessian.subs([(x,stationary_points[i][0]),(y,stationary_points[i][1])]).evalf()

    if sign_det_hessian > 0:

        sign_f_xx = f_xx.subs([(x,stationary_points[i][0]),(y,stationary_points[i][1])]).evalf()

        if sign_f_xx > 0:

            print('停留点:{0}はf(x,y)の極小点'.format([stationary_points[i][0],stationary_points[i][1]]))

        elif sign_f_xx < 0:

            print('停留点:{0}はf(x,y)の極大点'.format([stationary_points[i][0],stationary_points[i][1]]))

        else:

            print('この方法では判定不可能')

    elif sign_det_hessian < 0:

        print('停留点:{0}はf(x,y)の鞍点'.format([stationary_points[i][0],stationary_points[i][1]]))

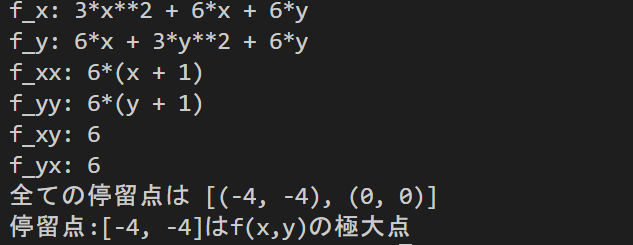
あってたが、意味わからないですね。目で見てもわからないですね。ハンカチが宙に舞ってるイメージしか浮かばない...

極限になっているか確かめる

極限になっているかどうか確かめました。
極座標を用いてx=rcosθ　y=2rsinθを用いました
分母の値や状況で極座標の値を変えて三角関数の公式などを作って約分とかやってみてください。ちなみに収束値は２です

\lim_{(x,y)\to (0,0)}\frac{x^3-8y^3+2x^2+8y^2}{x^2+4y^2}

import sympy as sym
import math
sym.init_printing()
Pi = sym.S.Pi # 円周率
E = sym.S.Exp1 # 自然対数の底
I = sym.S.ImaginaryUnit # 虚数単位
oo = sym.oo # 無限大

# 使用する変数の定義(小文字1文字は全てシンボルとする)
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z) = sym.symbols('a b c d e f g h i j k l m n o p q r s t u v w x y z')

import numpy as np
import matplotlib.pyplot as plt
c=(x**3-8*y**3+2*x**2+8*y**2)/(x**2+4*y**2)
d=sym.limit(c,x,0)
print('{0}'.format(d))
dd=sym.limit(d,y,0)
e=sym.limit(c,y,0)
ee=sym.limit(e,x,0)
print('{0}'.format(e))
if dd == ee :
    print('関数の極限は存在します')
    f=c.subs([(x,X),(y,1/2*Y)]).trigsimp() # 簡略化は必要(1行ずつやった方がいい)
    g=np.abs(sym.limit(f-ee,r,0))
    print('{0}'.format(g))
else :
    print('関数の極限は存在しません')

この実行結果は無事に関数の極限は存在しますと表示されますが、極限が存在しない時は、どのように実行されるかは検証しておりません。頑張ります。

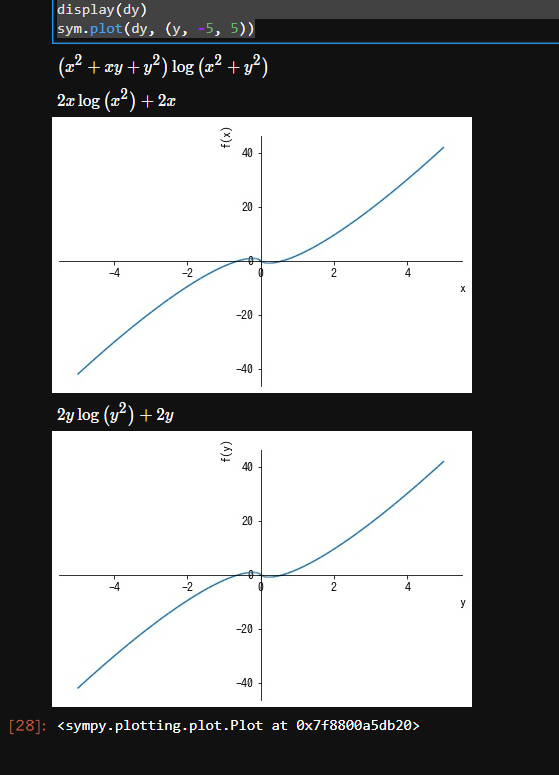
原点に関して偏微分可能かの実行結果

(x^2+xy+y^2)\log(x^2+y^2)

のxとｙそれぞれ偏微分してみました。

from sympy import *
import sympy as sym
import math
from IPython.display import display, Latex
x=Symbol('x')                  # 文字'x'を変数xとして定義
y=Symbol('y')                 # 文字 'y'を変数yとして定義

f = (x ** 2 + x * y + y ** 2) * sym.log(x ** 2 + y ** 2)

display(f)

dx = sym.diff(f, x).subs({y: 0})
dy = sym.diff(f, y).subs({x: 0})

display(dx)
sym.plot(dx, (x, -5, 5))

display(dy)
sym.plot(dy, (y, -5, 5))

これはteratailで質問を受け付けたところ、解答を得ることができました。ありがとうございました。ｘとｙを偏微分すると両方とも原点通っているので原点に対して偏微分可能となってますね。わかりやすい。

感想

只々pythonめっちゃ便利でした。ほかの言語と比べるとライブラリたっぷり、本当にすごい。次は理論を加えていきたいと思います。今回も紹介程度となってしまった。もっと応用的なものをやっていきたいですね。
めんどくさい計算や、検算する時はこのコードを使っていきますかね。次はラグランジュの未定乗数法やガウス分布のなんかよくわからんやつを分散や平均の値を変えて色々いじってめためた為になる様なコードでも書いていこうかな。
実力があればの話ですがね！

参考サイトや質問など

https://qiita.com/tibigame/items/aebbac176d9bbdaf3d15
https://qiita.com/hiroyuki_mrp/items/d373b951e216f62c4957
https://qiita.com/PlanetMeron/items/63ac58898541cbe81ada
https://short4010.hatenablog.com/entry/2019/05/12/142731
自分のアカウントです
https://teratail.com/questions/283867