前回まで
改めて
機械学習を始めるにも、算数や数学がわからないと、入門書すら読めない。ただそこまで、ちゃんと解説してあるものもない。ということで最低限必要な数学基礎をこの記事で書けたらいいなと思っています。
環境
ほぼ影響ないですが、python3系を利用。
前提
四則演算や累乗(2乗とか3乗とか)がわかっていること。
極限について
$\displaystyle \lim_{x \to 0}$
とかいうやつです。
変数xを限りなく一定の値に近づけたときに、f(x)が一定の値αに近づいていくことを「収束」と言い、このαのことを極限値といいます。
わかりやすい例でいうと
$f(x) = \frac{x^2-x-2}{x^3-8}$
という関数が会ったときに、x=2だとすると、分子も分母も0となるので
$\frac{0}{0}$となってしまい、「値を導くことができない」のです。
これをlimを使って考えてみます。
まず因数分解を行います。$x=2$ではないので、(x-2)を約分することが出来る。
$\frac{x^2-x-2}{x^3-8} = \frac{(x-2)(x+1)}{(x-2)(x^2+2x+4)}=\frac{x+1}{x^2+2x+4}$
これを元に極限値を求めます。
$\displaystyle \lim_{x \to 2}\frac{x^2-x-2}{x^3-8}$
$=\displaystyle \lim_{x \to 2}\frac{x+1}{x^2+2x+4}$
$=\frac{2+1}{2^2+2\times2+4}$
$= \frac{3}{12}$
$= \frac{1}{4}$
微分について
微分とは、「ある瞬間の変化」を求めることです。
例えば、「お湯を沸かす」事象について考えてみます。
ある瞬間の温度上昇について、tが時間、x(t)が時間tの時の温度とすると
瞬間上昇温度
$= \displaystyle \lim_{\Delta t \to 0}\frac{\Delta x}{\Delta t}$
$= \displaystyle \lim_{\Delta t \to 0}\frac{x(t+\Delta t)-x(t)}{\Delta t}$
というように表すことができ、ある時点の変化を表すことができます。$\Delta$は変化を表しています。$lim$ではその変化を限りなく小さくしています。
これらと同様に、二次関数や三次関数などの、ある瞬間の変化を表すことができ、それを「導関数」と呼びます。つまりxが少しだけ変化した時の、yもしくはf(x)の変化を量を求めるということです。そして導関数を求める作業を「微分」と言います。
$\frac{d(x)}{dx}=f'(x) = \displaystyle \lim_{\Delta x \to 0}\frac{\Delta f(x)}{\Delta x}=\displaystyle \lim_{\Delta h \to 0}\frac{f(x+h)-f(x)}{h}$
公式
$y = x^r$
を微分すると
$\frac{dy}{dx} = rx^{r-1}$
$\frac{d}{dx}(f(x)+g(x)) = \frac{df(x)}{dx}+\frac{dg(x)}{dx}$
$\frac{d}{dx}(kf(x)) = k\frac{df(x)}{dx}$
ようは分母で書かれた変数で、分子(もしくは横に出てるもの)を微分してあげるだけです!
もし変数が式中に複数ある場合は、分母にある変数で微分をする(偏微分)を行えばいいです。偏微分ではラウンドデルタを使います。
$f(x,y) = 2x^2+4xy+2y^3$
xで微分する時はyを定数としてみなします。
$f'(x,y) = \frac{\partial f(x,y)}{\partial x} = 4x+4y$
yで微分する時はxを定数としてみなします。
$f'(x,y) = \frac{\partial f(x,y)}{\partial y} = 4x+6y^2$
接線の傾き
$y= x^2$の(2,4)における接線の方程式を求める
微分すると
$f'(x) = \frac{dy}{dx} = 2x$
これが傾きの方程式。つまりf'(2) = 4。
接線は$y = 4x+b$になり、yは元の(2,4)と書いてある通りなので$4 = 8 + b$となり$b = 4$であることがわかる。まとめると$y = 4x-4$という事になる。
極値
微分した時の導関数が0を取りうる時、元の関数は「極値」を取ります。
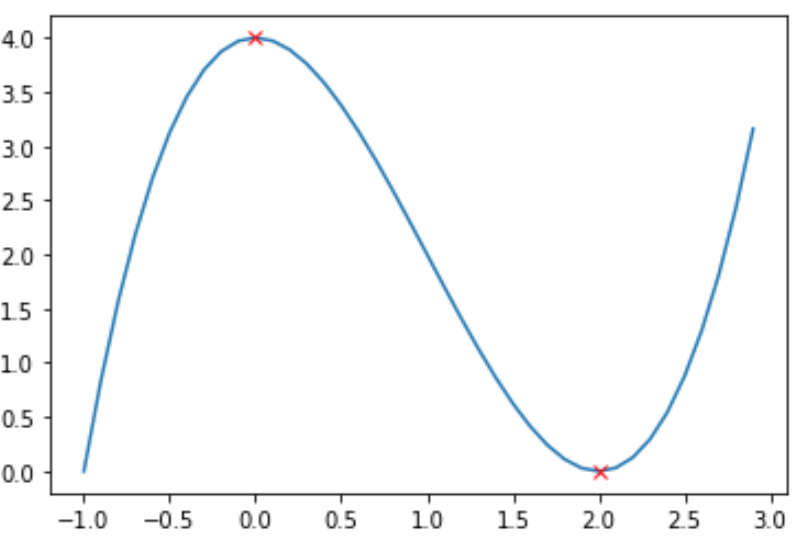
pythonで考えてみる
$x^3-3x^2+4$
x = np.arange(-1,3,0.1)
y = (x**3) - (3*x**2) +4
plt.plot(x,y)
plt.plot(0,4,marker = "x",color = "red")
plt.plot(2,0,marker = "x",color = "red")
1階微分
$f'(x) = 3x^2-6x$
$= 3x(x-2)$
x = np.arange(-1,3,0.1)
y_d = 3*x**2-6*x
plt.plot(x,y_d)
plt.plot(0,0,marker = "x",color = "red")
plt.plot(2,0,marker = "x",color = "red")
plt.plot(1,-3,marker = "x",color = "red")
plt.hlines(0,-1,3,color = "red")

計算式とグラフを見ると(0,2)で0を取ります。ということは微分前の$x^3-3x^2+4$でも0,2のところが極大値もしくは極小値になります。
さらに微分をした2階微分
$f''(x) = 6x^6$
$= 6(x-1)$
x = np.arange(-3,3,0.1)
y_d = 6*x-6
plt.plot(x,y_d)
plt.plot(1,0,marker="x",color = "red")
plt.hlines(0,-3,1,color = "red")
同様に1の時に0を取っているので、ということは元の$f'(x) = 3x^2-6x$でも1のところが極小値になります。

関数の微分
・$x^r$ -> $rx^{r-1}$
・$e^x$ -> $e^x$ ★
・$a^x$ -> $a^x log_e a$
・$log_e x$ -> $\frac{1}{x}$★
・$sinx$ -> $cosx$ -> $-sinx$ -> $-cosx$ -> $sinx$
・$tanx$ -> $\frac{1}{cos^x}$
※★がついてるところはよく式の変換で使われている(気がする)
※三角関数の部分に関しは循環しているので、4回微分したら元に戻る
pythonでやってみる。tanの微分は商の微分を使っています。
import sympy as sym
# 記号化
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z)=sym.symbols("a b c d e f g h i j k l m n o p q r s t u v w x y z")
sym.diff(x**2,x)
# →2x
sym.diff(sym.exp(x),x)
# →𝑒**2
sym.diff(sym.log(x))
# ->1/x
sym.diff(sym.sin(x))
# ->cos(𝑥)
チェーンルール・合成関数
$\frac{dy}{dx}=\frac{dy}{du}・\frac{du}{dx}$
この公式を使うときは、変数が1つの時です。uというものが出てきますが、これは中の式をまとめたものになります。右辺の左で関数全体を、右辺の式でuを微分します。置き換える式がたくさんある場合は掛け算もその分伸びます。
例)
$(3x-2)^5$の微分では、$u=(3x-2)$として$u^5$と置きます。その後「$u^5$をuで微分したもの」と「(3x-2)をxで微分したもの」を掛け合わせます。
=> $\frac{du^5}{du}・\frac{du}{dx}$
$=5u^4・3=$
$=5(3x-2)^4・3$
$=15(3x-2)^4$
とすることができます。
・$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}・\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}・\frac{\partial v}{\partial x}$
この公式を使うときは、変数が多変数の時です
例)
$(4x+3)^2+(x+y+2)^3$の微分では、$u=(4x+3),v=(x+y+2)$として$u^2+v^3$と置きます。その後「$u^2$をuで微分したもの」と「(4x+3)をxで微分したもの」を掛け合わせ、さらに「$v^3$をvで微分したもの」と「(x+y+2)をxで微分したもの」を掛け合わせます。
=> $\frac{du^2}{du}・\frac{du}{dx}+\frac{dv^3}{dv}・\frac{dv}{dx}$
$=2u・4+3v^2・1$
$=2(4x+3)・4+3(x+y+2)^2・1$
$=8(4x+3)+3(x^2+y^2+2^2+2xy+4x+4y)$
$=32x+24+3x^2+3y^2+12+6xy+12x+12y$
$=3x^2+44x+6xy+3y^2+12y+36$
$=3x^2+(44+6x)y+3y^2+12y+36$
とすることができます。
・$\frac{d}{dx}(f(x)g(x))=\frac{df(x)}{du}g(x)+f(x)\frac{dg(x)}{dx}$
例)
いわゆる積の微分法というものになります。
$x\sin{x}$の微分では、$f(x)=x,g(x)=\sin{x}$として$y=f(x)g(x)$と置き計算をしていきます。
=>$\frac{dy}{dx}$
$=\frac{df(x)}{dx}g(x)+f(x)\frac{dg(x)}{dx}$
$=1⋅\sin{x}+x⋅\cos{x}$
$=\sin{x}+x\cos{x}$
とすることができます。これはよく出てくるやつです。他にもこういう頻出のがあります。
活性化関数と微分
以前取り扱ったシグモイド関数の微分について取り上げたいと思います。
まず微分してみます。
$f(x) = \frac{1}{1+e^{-ax}}$
において$u = 1+e^{-ax},v = -ax$
としておいた上で、$f(x) = \frac{1}{u} = u^{-1}$と式を変換しておきます。
今回は2つの置き換えたのでチェーンルールもその分長く適用します。
$f'(x) = \frac{df(x)}{du}・\frac{du}{dv}・\frac{dv}{dx}$
となります。計算を進めていきます。
$f'(x) = \frac{du^-1}{du}・\frac{d(1+e^v)}{dv}・\frac{d(-ax)}{dx}$
$= -u^{-2}・e^v・-a$
$= u^{-2}・e^v・a$
$= \frac{1}{u^2}・e^v・a$
$= \frac{a・e^v}{u^2}$
置き換えたものを代入します。
$= \frac{a・e^{-ax}}{(1+e^{-ax})^2}$
となります。さらに変形させるともっとシンプルにかけます。
(この変形の仕方以外にもありますが)まず$+a-a$という式を付け足します。
$= \frac{a・e^{-ax}+a-a}{(1+e^{-ax})^2}$
その次にaを頭に出します。
$= \frac{a(1+e^{-ax})-a}{(1+e^{-ax})^2}$
ちょっとわかりやすく変形しておきます。
$= \frac{a(1+e^{-ax})}{(1+e^{-ax})^2}-\frac{a}{(1+e^{-ax})^2}$
左側を約分しておきます。
$= \frac{a}{(1+e^{-ax})}-\frac{a}{(1+e^{-ax})^2}$
この後がわかりづらいですが$\frac{a}{(1+e^{-ax})}$を頭に出します。
$= \frac{a}{(1+e^{-ax})}\bigg(1-\frac{1}{(1+e^{-ax})}\bigg)$
$= a\frac{1}{(1+e^{-ax})}\bigg(1-\frac{1}{(1+e^{-ax})}\bigg)$
かなり見覚えのある感じ。最後にシグモイド関数の部分をf(x)に置き換えます。
$= af(x)(1-f(x))$
つまり$\varsigma(x)$の微分は$\varsigma'(x)= a\varsigma(x)(1-\varsigma(x))$で表せるということになります。
ついでもう一回微分(二階微分)すると$\varsigma''(x) = a^2\varsigma(x)(1-\varsigma(x))(1-2\varsigma(x))$という式になります。
この1階微分の式の最大値は0.25になります。(a=1の標準シグモイド、$\varsigma(x) = \frac{1}{2}$を当てはめるだけ)
このようなシグモイド関数は、活性化関数(NNの重みの調整時に使う)として利用されますが、上記のように最大値が0.25なのでNN層の深さによっては誤差伝播せず勾配消失してしまうので、ランプ関数(ReLU)が使われたります。ランプ関数は微分すると最大1最小0をとるので活性化関数としてとても使い勝手がとても良いです。
import sympy as sym
# 記号化
(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z)=sym.symbols("a b c d e f g h i j k l m n o p q r s t u v w x y z")
a = 1
sym.diff(1/(1+sym.exp(-x*a)))
# -> e^-x/(1+e^-x)^2
ここまで
微分は最小二乗法やNNの誤差逆伝播法などでも使うので、必ず必要になる大事な部分でした。積分はまた投稿します。
次回はベクトルについて記載していきます。