[python]算数・数学②~平方根・指数・対数~

前回まで

前回はこちら

改めて

機械学習を始めるにも、算数や数学がわからないと、入門書すら読めない。ただそこまで、ちゃんと解説してあるものもない。ということで最低限必要な数学基礎をこの記事で書けたらいいなと思っています。

環境

ほぼ影響ないですが、python3系を利用。

前提

四則演算や累乗（2乗とか3乗とか）がわかっていること。

平方根(ここはpython省略します。)

ざっと公式

<公式>

$\sqrt{a}^2 = a$

$
a\times\sqrt{b} = a\sqrt{b}
$

$
b\sqrt{a}+c\sqrt{a} = (b+c)\sqrt{a}
$

$
\sqrt{a}\times\sqrt{b} = \sqrt{ab}
$

$
\sqrt{a}\div\sqrt{c} = \frac{\sqrt{a}}{\sqrt{c}} = \sqrt{\frac{a}{c}}
$

$
\sqrt{a^2\times{b}} = a\sqrt{b}
$

整数同士、平方根同士をかけて計算する

$
a\sqrt{b}\times c\sqrt{d} = a\times{c}\sqrt{b\times{d}}
$

累乗(ここはpython省略します。)

こういうやつのことで、aを底（てい）と呼び、pを指数という。
$
a^p
$

また4は64の3乗根といい、2は4の2乗根という。2乗根の場合は省略できる

$\sqrt[3]{64} = 4$
$\sqrt[2]{4} = \sqrt{4} = 2$

ざっと公式

<公式>

$
a^0 = 1
$

$
a^p \times{a^q} = a^{p+q}
$

$
{(a^p)}^{q} = a^{pq}
$

$
{(ab)}^{p} = a^{p}\times{b^{p}}
$

$
{a}^{-p} =\frac{1}{a^p}(★重要)
$

$
\sqrt[p]{a}\times{\sqrt[p]{b}}=\sqrt[p]{ab}
$

$
\sqrt[q]{\sqrt[p]{a}}=\sqrt[pq]{a}
$

$
\sqrt[p]{a}={a}^{\frac{1}{p}}(★重要)
$

[補足]nの0乗について

累乗が増えていくとどうなるか。

3^1,3^2,3^3,3^4,,3^5\
= 3,9,27,81,243

のように3倍の等比数列になっている。であれば$3^0$は等比数列で逆に進めばいいだけ($\frac{1}{3}$倍) すれば良いので$3^0=1$であり$n^0=1$になる

[補足]二乗根の2乗について

$
\sqrt[2]{a}=\sqrt{a} = {a}^{\frac{1}{2}} →(\sqrt{a})^2 = ({{a}^{\frac{1}{2}}})^2= (a)^{\frac{1}{2}\times{2}}= a
$

###公式を使えば簡単に計算できる
$4^8\times{2^{-1}}\div{2^4} $
$ ={(2^2)}^8 \times{2^{-1}}\times{\frac{1}{2^4}}$
$= {2}^{16} \times{2^{-1}}\times{2^{-4}}$
$= {2}^{(16-1-4)}$
$= {2}^{11}$

指数関数

指数関数（a>1で右上がり、0<a<1で右下がりになる）

$
y = a^x
$

以下は$y=2^x$

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(1,10,0.1)
y = 2**x
plt.plot(x,y)

以下は$y=\frac{1}{2}^x$

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(1,10,0.1)
y = 0.5**x
plt.plot(x,y)

ちなみにa<0の場合は、上下が逆さまになります。

ただ計算するだけなら
2の４乗は

math.pow(2, 4)

で表現できる。

対数関数

対数関数は、要は「xにするにはaを何乗すればいいのか。y乗だよねという式」
aを底といい、xを真数という。

$
y = \log_a{x}
$

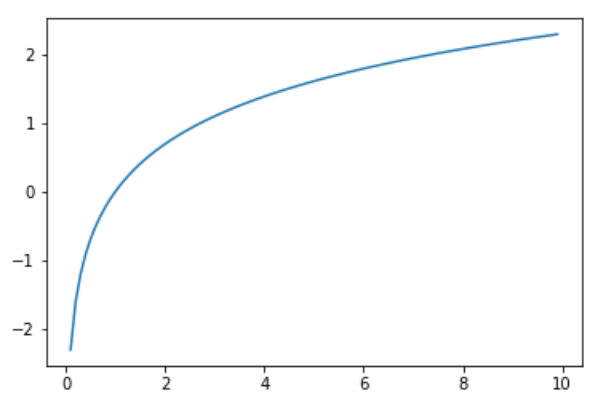
以下は$y=\log_e {x}$ 当然aの0乗(y)は1(x)になっています。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(0,10,0.1)
y = np.log(x)
plt.plot(x,y)

ざっと公式

<公式>

$
\log_a{a} = 1
$

$
\log_a{1} = 0
$

$
\log_a{XY} = \log_a{X} + \log_a{Y}
$

$
\log_a{\frac{X}{Y}} = \log_a{X} - \log_a{Y}
$

$
\log_a{{X}^p} = p\times{\log_a{X}}= p \log_a{X}
$

$
\log_a{X} = \frac{\log_c{X}}{\log_c{a}}
$

[補足]掛け算に変換される部分

$
\log_a{XY} = \log_a{X} + \log_a{Y}
$

$
\log_2{6} = \log_2{1\times{6}}=\log_2{1}+\log_2{6}=\log_2{6}
$

よく間違われるやつ**※間違い**

$
log_2(1+5) = log_2{1}+log_2{5} = log_2{5}
$

[補足]かけてあるものを頭に出す

$
\log_a{{X}^p} = p\times{\log_a{X}}= p \log_a{X}
$

$
\log_2{8} = \log_2{{2}^3} = 3\times{\log_2{2}}
$

文系に面倒くさがられる自然対数

ネイピア数eを底に取る対数のことを自然対数という
$
\log_e{X} = \ln{X}
$

そもそもネイピア数って
$
e = 2.718...
$くらいの数字

ちなみにこんな表現もします。みやすくなる
$
e^x = \exp{x} = \exp{(x)}
$

なんでこんなわけわからないネイピア数を用いるのか

理由1：微分したときに便利だから１(★重要)

eを底とする指数関数は微分しても同じ！！

$
\frac{d}{dx}e^x = e^x
$

理由2：微分したときに便利だから２(★重要)

自然対数を微分すると分数になる！！

$
\frac{d}{dx}\log_e{X} = \frac{1}{X}
$

------<証明してみます（長いので飛ばしていいです）>-------

※微分します。

$\frac{d}{dx}f(X) $
$= \lim_{h \to 0}\frac{f(x+h)-f(x)}{(x+h)-x}$
$= \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$
$= \lim_{h \to 0}\frac{log_e{(x+h)}-log_e{x}}{h}$
$= \lim_{h \to 0}\frac{1}{h}\times\frac{log_e{(x+h)}-log_e{x}}{1}$
$= \lim_{h \to 0}\frac{1}{h}\times({log_e{(x+h)}-log_e{x}})$
$= \lim_{h \to 0}\frac{1}{h}\times{log_e{\frac{(x+h)}{x}}}$　★公式
$= \lim_{h \to 0}\frac{1}{h}\times{log_e\bigg({\frac{x}{x}+\frac{h}{x}}\bigg)}$
$= \lim_{h \to 0}\frac{1}{x}\times{\frac{x}{h}}\times{log_e{(1+\frac{h}{x})}}$

$\frac{h}{x}$をtと置く($\frac{x}{h}$は$\frac{1}{t}$と置く)と(h→0の時t→0になる)

$
= \frac{1}{x}\lim_{t \to 0}{log_e{(1+t)}}^{\frac{1}{t}}　　
$　　★$\frac{1}{t}$乗は公式

と変形ができ($\frac{1}{x}$は$lim$に関係ないので外に出せる。)

$
\lim_{t \to 0}{(1+t)}^{\frac{1}{t}}=e
$

という特性がある ことから

$
= \frac{1}{x}log_e{e}\
= \frac{1}{x}
$
とすることができる

------------<証明終了>-------------

後半出てきた

$
\lim_{t \to 0}{(1+t)}^{\frac{1}{t}}=e
$

ですが

$
\lim_{t \to 0}{(1+\frac{1}{t})}^{t}=e
$
や
$
\lim_{t \to 0}{(1-\frac{1}{t})}^{t}=\frac{1}{t}
$
と表すことがある

常用対数

$log_{10} x$ のことを言います。

シグモイド関数

ロジスティック回帰で使われるものです。活性化関数として使われます。

以下のような関数をいい、aをゲインと呼び、a=1の時に標準シグモイド関数と呼びます。

$
\varsigma_a(x) = \frac{1}{1+\exp{(-ax)}} = \frac{1}{1+e^{-ax}}
$

xが負になるとyが０に近づき、xが正になるとyが１に近づく。
ちなみに0の時は$\frac{1}{2}$になる

一個ずつ式とコードを書くとわかりやすいのでやっていきます。

まず分母の一部　$e^x$　を考えます。普通に2.718..の累乗です。

import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# まず指数が増えれば指数関数も増えることを確認
x = np.arange(-5,5,0.01)
y_list = []
for i in x:
    y = math.exp(i)
    y_list.append(y)
plt.plot(x,y_list)

次にa=1とした時の$e^{-x}$を考えます。普通に$\frac{1}{2.718..^x}$なので割る数がどんどん増えていきますので、値は小さくなっていきます。

#指数が負の数を取るとき、xが増えれば指数関数が減ることを確認。どんどん0に近く
x = np.arange(-5,5,0.01)

y_list = []
for i in x:
    y = math.exp(-1*i)
    y_list.append(y)
plt.plot(x,y_list)

上の図は限りなく0近づいているわけですが、それに１を加えます。つまり限りなく１に近づくということです。$1+e^{-ax}$になります。

#シグモイドの分母で言えば、どんどん１に近く(グラフわかりづらいかも)
x = np.arange(-3,3,0.01)

y_list = []
for i in x:
    y = 1+math.exp(-1*i)
    y_list.append(y)
plt.plot(x,y_list)

最後に今まで計算していたものを分母にとります。つまりxがプラスにいけばいくほと分母が１に近づくので、式全体は1÷1=1の式に近づきます。逆を考えるとxがマイナスにいけばいくほど限りなく分母が大きくなれば、式全体は０に近づきます。
※xが0を取る時は、$1+e^0=2$になるので、全体は$\frac{1}{2}$になります。

#シグモイド全体
x = np.arange(-5,5,0.01)

y_list = []
for i in x:
    y = 1/(1+math.exp(-1*i))
    y_list.append(y)
plt.plot(x,y_list)

ここまで

参考書のなかでは当然説明なく変形されていたりするので、ここら辺の内容はすごく大事です。
※不明点や不備があればコメントください。

次回は三角関数について投稿していきます。